1
1990
... 非线性演化方程已被用于描述现代科学的许多复杂现象, 如流体力学, 凝聚态, 生物学和光通信[1⇓-3]. Korteweg-de Vries (KdV) 方程 ...
1
1991
... 非线性演化方程已被用于描述现代科学的许多复杂现象, 如流体力学, 凝聚态, 生物学和光通信[1⇓-3]. Korteweg-de Vries (KdV) 方程 ...
1
2008
... 非线性演化方程已被用于描述现代科学的许多复杂现象, 如流体力学, 凝聚态, 生物学和光通信[1⇓-3]. Korteweg-de Vries (KdV) 方程 ...
On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves
1
1895
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Korteweg-de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation
1
1968
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Korteweg-de Vries equation and generalizations. II. Existence of conservation laws and constants of motion
2
1968
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
... mKdV 方程在许多领域都具有重要应用, 如模拟光纤中的超连续谱产生[12], 蜿蜒洋流[13] 和多组分等离子体[14]. 当同时考虑二次和三次非线性项时, KdV 方程成为 KdV 和 mKdV 方程的组合 KdV-mKdV 方程, 也称为 Gardner 方程[6,15] ...
Korteweg-de Vries equation and generalizations. III. Derivation of the Korteweg-de Vries equation and Burgers equation
1
1969
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Korteweg-de Vries equation and generalizations. IV. The Korteweg-de Vries equation as a Hamiltonian system
1
1971
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Obliquely propagating ion-acoustic solitons in a multi-component magnetized plasma with negative ions
1
1994
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Formulation of the Korteweg-de Vries and the Burgers equations expressing mass transports from the generalized Kawasaki-Ohta equation
1
2002
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Internal solitons in the ocean and their effect on underwater sound
1
2007
... 是非线性科学中的一个关键模型, 它解决了线性色散和非线性对流之间的平衡[4⇓⇓⇓-8], 已广泛应用于等离子体中的等离子声波[9], 化学反应理论中的质量传递[10] 和海洋中的浅水波[11] 等各个方面. 由于 KdV 方程只包含二次非线性, 但在一些复杂的环境情况下必须考虑高阶非线性效应, 因此研究人员提出了修正后的 KdV(mKdV) 方程 ...
Models for supercontinuum generation beyond the slowly-varying-envelope approximation
1
2014
... mKdV 方程在许多领域都具有重要应用, 如模拟光纤中的超连续谱产生[12], 蜿蜒洋流[13] 和多组分等离子体[14]. 当同时考虑二次和三次非线性项时, KdV 方程成为 KdV 和 mKdV 方程的组合 KdV-mKdV 方程, 也称为 Gardner 方程[6,15] ...
Predicting eddy detachment for an equivalent barotropic thin jet
1
1994
... mKdV 方程在许多领域都具有重要应用, 如模拟光纤中的超连续谱产生[12], 蜿蜒洋流[13] 和多组分等离子体[14]. 当同时考虑二次和三次非线性项时, KdV 方程成为 KdV 和 mKdV 方程的组合 KdV-mKdV 方程, 也称为 Gardner 方程[6,15] ...
Nonlinear ion-acoustic waves in multicomponent plasmas
1
1988
... mKdV 方程在许多领域都具有重要应用, 如模拟光纤中的超连续谱产生[12], 蜿蜒洋流[13] 和多组分等离子体[14]. 当同时考虑二次和三次非线性项时, KdV 方程成为 KdV 和 mKdV 方程的组合 KdV-mKdV 方程, 也称为 Gardner 方程[6,15] ...
Interactions of breathers and solitons in the extended Korteweg-de Vries equation
1
2005
... mKdV 方程在许多领域都具有重要应用, 如模拟光纤中的超连续谱产生[12], 蜿蜒洋流[13] 和多组分等离子体[14]. 当同时考虑二次和三次非线性项时, KdV 方程成为 KdV 和 mKdV 方程的组合 KdV-mKdV 方程, 也称为 Gardner 方程[6,15] ...
Bright and dark rogue internal waves: The Gardner equation approach
1
2019
... 它可以用来描述非线性科学中的各种现象, 例如大振幅内波[16], 等离子体中的波动现象[17]和量子流体动力学[18]. 为了研究更一般情况下的 Gardner 方程, 在本文中我们讨论广义 Gardner 方程[19] ...
Symbolic computation of exact solutions in hyperbolic and elliptic functions for nonlinear PDEs
1
2004
... 它可以用来描述非线性科学中的各种现象, 例如大振幅内波[16], 等离子体中的波动现象[17]和量子流体动力学[18]. 为了研究更一般情况下的 Gardner 方程, 在本文中我们讨论广义 Gardner 方程[19] ...
Semiclassical solitons in strongly correlated systems of ultracold bosonic atoms in optical lattices
1
2011
... 它可以用来描述非线性科学中的各种现象, 例如大振幅内波[16], 等离子体中的波动现象[17]和量子流体动力学[18]. 为了研究更一般情况下的 Gardner 方程, 在本文中我们讨论广义 Gardner 方程[19] ...
New exact solutions for generalized Gardner equation
2
2017
... 它可以用来描述非线性科学中的各种现象, 例如大振幅内波[16], 等离子体中的波动现象[17]和量子流体动力学[18]. 为了研究更一般情况下的 Gardner 方程, 在本文中我们讨论广义 Gardner 方程[19] ...
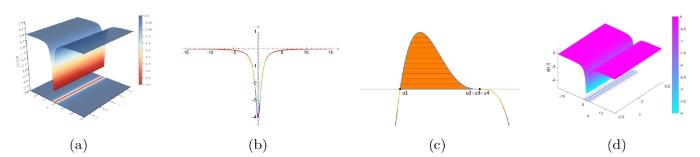
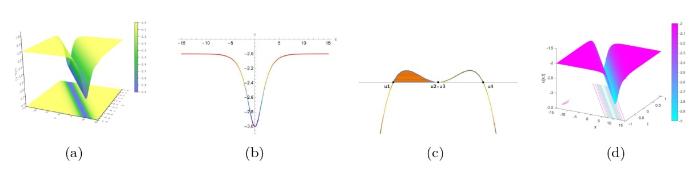
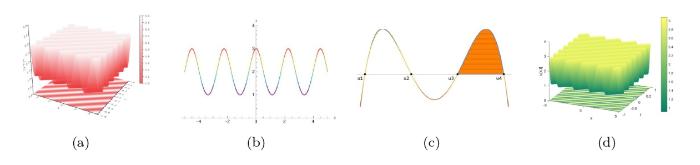
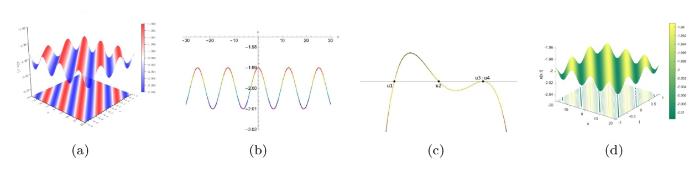
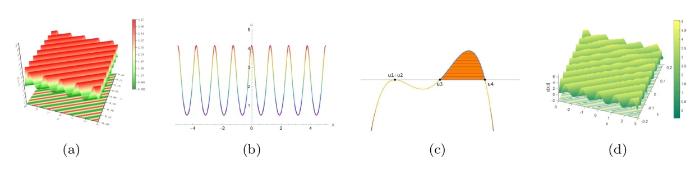
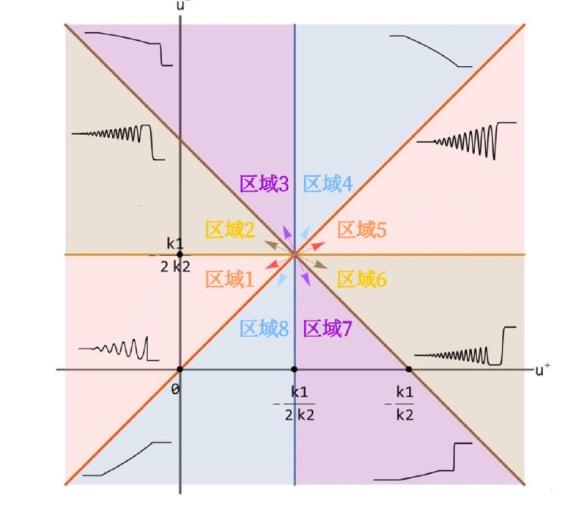
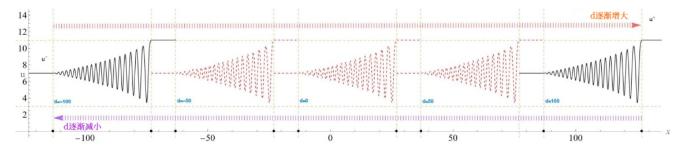
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
1
2002
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
Solitary waves on a two-layer fluid
1
1978
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
Analytical solutions of long nonlinear internal waves: Part I
1
2011
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
Generation of large-amplitude solitons in the extended Korteweg-de Vries equation
1
2002
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
A family of completely integrable multi-Hamiltonian systems explicitly related to some celebrated equations
1
2001
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
Painlevé analysis, Lax pair, B?cklund transformation and multi-soliton solutions for a generalized variable-coefficient KdV-mKdV equation in fluids and plasmas
1
2012
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
Lax pair, B?cklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation
2
2007
... 其中 u(x, t) 表示复值波函数, 自变量 x 和 t 代表空间和时间, 线性和非线性项的系数 d , k_1 和 k_2 可以为任意正数或负数, 但色散系数 c 始终为正数, 这些系数可以通过稳定海洋背景密度的流动分层来描述[19⇓⇓⇓-23]. 当系数满足一定条件约束时, 广义 Gardner 方程已被证明是可积的, Lax 对和其他所需的完全可积性质已经被证明[24⇓-26]. 当给定 KdV 方程一组初始条件时, 方程的孤子解具有与初始条件无关的固定极性. 然而, 广义 Gardner 方程可以通过以下变换保持不变 ...
... 有限间隙积分方法是在与可积非线性色散方程有关的线性谱问题中获得周期或拟周期解的方法之一, 并在数学物理中的各种渐近问题中与势能递减的薛定谔算子具有重要的应用[51]. 当利用有限间隙积分方法得到的周期解或准周期解研究 Whitham 调制理论时, 如果准周期解的频谱带端点随 x 和 t 变化缓慢则可将其称为 Whitham 调制方程的黎曼不变量, 从而得到与线性光谱问题相关的可积方程的周期解所需的黎曼不变量参数化[42]. 广义 Gardner 方程对应的 Lax 对如下[26] ...
Dispersive shock waves and modulation theory
1
2016
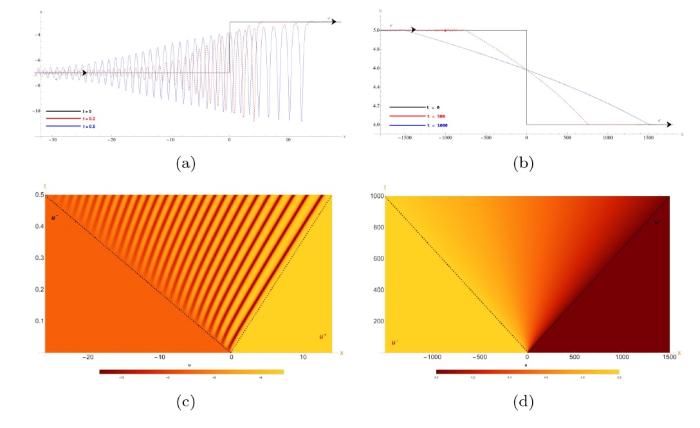
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone
1
1999
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
Observation of very large and steep internal waves of elevation near the Massachusetts coast
1
2004
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
On the solitary wave paradigm for tsunamis
1
2008
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
The morning glory of the Gulf of Carpentaria: a paradigm for non-linear waves in the lower atmosphere
1
1992
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
Hydraulic jump and undular bore formation on a shelf break
1
1988
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
2
1974
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
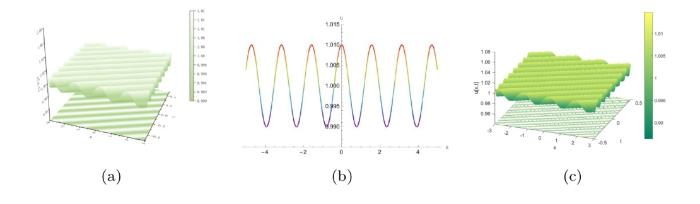
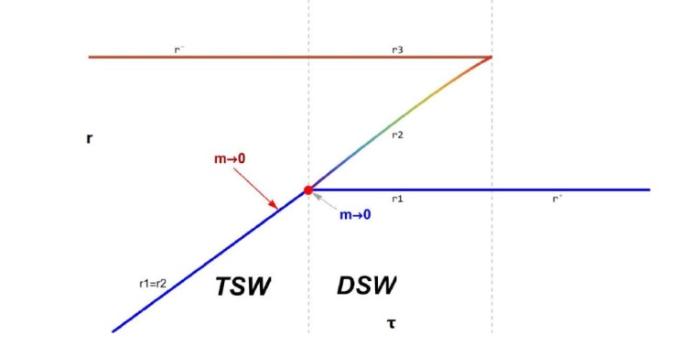
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Non-linear dispersive waves
1
1965
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
Dispersive shock waves governed by the Whitham equation and their stability
1
2018
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
Dispersive and diffusive-dispersive shock waves for non-convex conservation laws
1
2017
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
1
2016
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
Nonstationary structure of a collisionless shock wave
1
1974
... 冲击波是由于物理量初始突变而产生的一种普遍物理现象. 在水波和超流体等介质中, 非线性往往会产生由色散介导的破碎波从而可能导致相干结构的不稳定, 这种相干结构通常被称为色散冲击波 (DSW) , 也可以称为波状孔, 无耗散冲击波或无碰撞冲击波[27]. 随着分散流体力学的发展, 色散冲击波已被发现在潮汐演化[28], 海洋运输[29], 海啸传播[30], 雷暴引发[31]和半日内潮[32]中发挥着重要作用. 色散冲击波在色散介质中可以通过 Whitham 调制理论来研究[33], 这是一种连接两种不同基本流动状态并随时间和空间缓慢演化的非线性调制波列, 其中波数, 波长, 振幅和频率等调制参数的缓慢演化由流体动力学平均方程控制, 也称之为 Whitham 调制方程[34]. Whitham 调制方程可以构成一个偏微分方程组, 如果该系统是椭圆型的, 则非线性调制波列是调制不稳定的, 但如果该系统是双曲型, 则色散冲击波可以表现为调制方程的简单波解, 并且波列是调制稳定的[35]. 由于色散冲击波是在弱色散非线性介质中形成的非平稳波列, 非线性导致前沿逐渐变陡并在弱色散的影响下发生梯度突变, 最终形成陡峭的梯度. 此时, 强振荡将由特征扇形中时空平面中的色散扩散引起, 其中扇形的边界代表色散冲击波的后沿和前沿. 然而, 在较小的空间和时间范围内观察时, 色散冲击波将表现为周期或准周期结构[36]. 色散冲击波中非线性的显著特性是它在后沿和前沿至少有两种不同的传播速度, 根据非线性和色散效应之间的平衡, 振幅趋于零的线性色散波出现在色散冲击波的后沿, 前沿则出现振荡波列的最大振幅[37,38]. ...
New approach to periodic solutions of integrable equations and nonlinear theory of modulational instability
1
1997
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Periodic solutions and Whitham modulation equations for the Lakshmanan-Porsezian-Daniel equation
1
2022
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Whitham modulation theory and periodic solutions for the fifth-order nonlinear Schr?dinger equation in the Heisenberg ferromagnetic spin chain
1
2023
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
The complete classification of solutions to the Riemann problem of the defocusing complex modified KdV equation
4
2022
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
... 有限间隙积分方法是在与可积非线性色散方程有关的线性谱问题中获得周期或拟周期解的方法之一, 并在数学物理中的各种渐近问题中与势能递减的薛定谔算子具有重要的应用[51]. 当利用有限间隙积分方法得到的周期解或准周期解研究 Whitham 调制理论时, 如果准周期解的频谱带端点随 x 和 t 变化缓慢则可将其称为 Whitham 调制方程的黎曼不变量, 从而得到与线性光谱问题相关的可积方程的周期解所需的黎曼不变量参数化[42]. 广义 Gardner 方程对应的 Lax 对如下[26] ...
... 我们可以通过波数守恒定律[42]推导出 Whitham 特征速度 v_i( r) 的表达式 ...
... 通过上面的分析发现方程 (1.4) 和 KdV 方程的 Whitham 特征速度十分相似[42], 但调制周期波的动力学特性却有很大的不同. 实际上, 为了研究方程 (1.4) 在不同区域的调制周期解, 需要利用推导出来的 u_j 和 r_i 之间的关系, 相同的调制解 r_i 可以导致方程 (1.4) 产生两种不同的调制解 u_j , 这在与 Hopf 方程 \psi _t+6\psi \psi _x=0 相关的无色散极限 ...
Dispersive shock wave theory for nonintegrable equations
1
2019
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Theory of optical dispersive shock waves in photorefractive media
1
2007
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Modulational instability of cnoidal wave solutions of the modified Korteweg-de Vries equation
2
1975
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
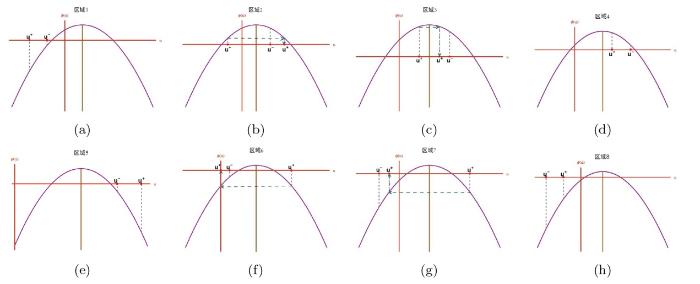
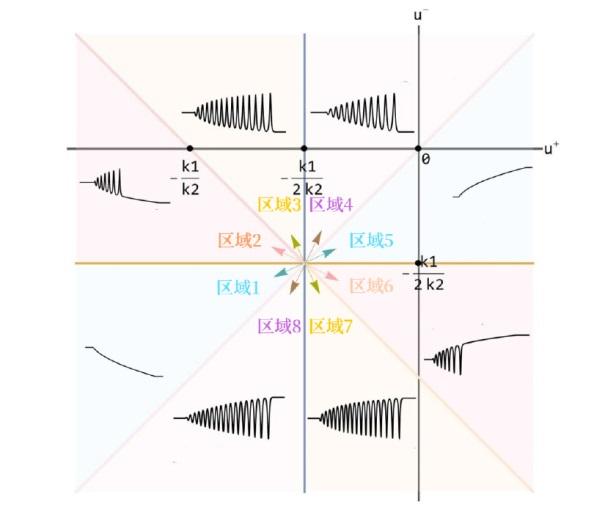
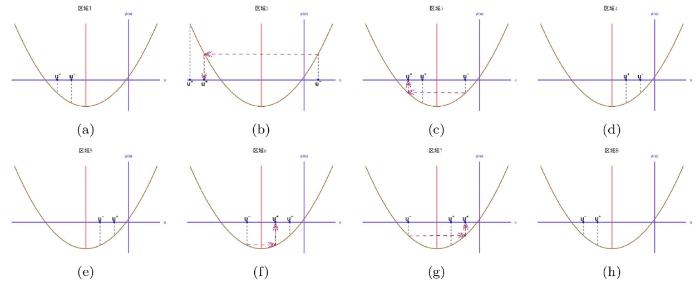
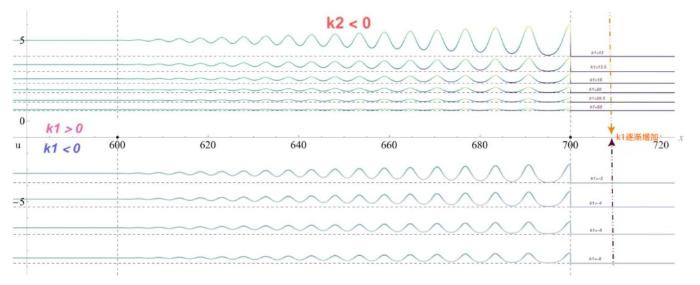
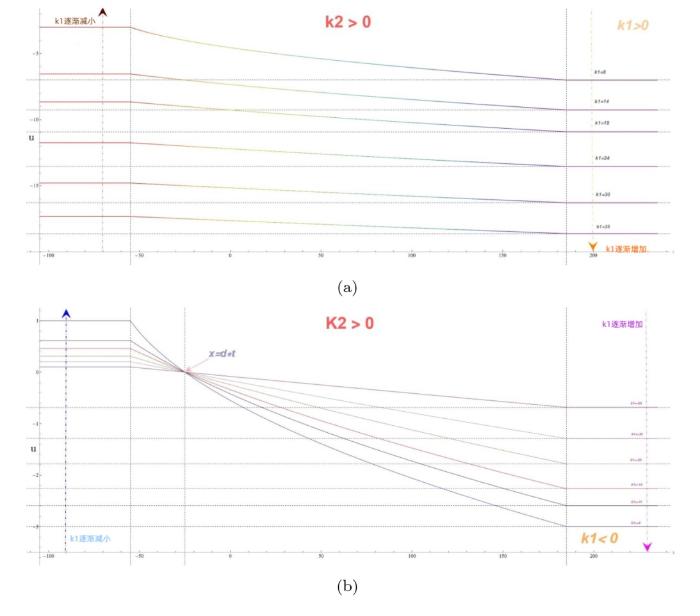
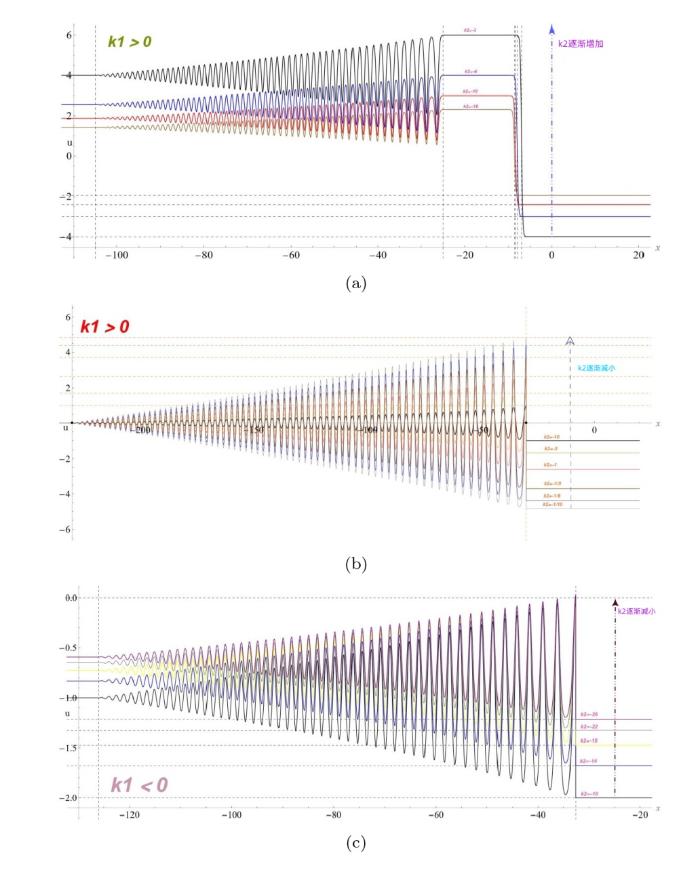
... 中是很明显的, 这是通过由 \psi(u) =\frac{1}{6}(k_2u^2+k_1u+d) 指定的映射 u\mapsto \psi 实现的. 当 u<-\frac{k_1}{2k_2} 或 u>-\frac{k_1}{2k_2} 时, \psi(u) 处于单调递增或单调递减区域. 广义 Gardner 方程的系统既不是椭圆型也不是双曲型, 这与 KdV 方程的 Whitham 调制系统不同并且调制动力学在不同的单调区域更加丰富. 当 k_2>0 时, 谱特征值 \lambda _i 可以为复数, 方程 (1.4) 的 Whitham 调制系统是椭圆型的从而导致调制不稳定性[45]. 对于具有实数初值的聚焦 mKdV 方程, 初值问题的零色散极限中产生的调制方程是双曲型的的进而保证了调制系统的稳定性, 并使得色散冲击波的进一步研究成为可能[47,53]. 由于 Gardner 方程可以转化为聚焦 mKdV 方程[50], 我们将假设广义 Gardner 调制方程的双曲性来解决所研究的初始不连续问题. ...
On dissipationless shock waves in a discrete nonlinear Schr?dinger equation
1
2004
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Undular bores and the initial-boundary value problem for the modified Korteweg-de Vries equation
4
2008
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
... 中是很明显的, 这是通过由 \psi(u) =\frac{1}{6}(k_2u^2+k_1u+d) 指定的映射 u\mapsto \psi 实现的. 当 u<-\frac{k_1}{2k_2} 或 u>-\frac{k_1}{2k_2} 时, \psi(u) 处于单调递增或单调递减区域. 广义 Gardner 方程的系统既不是椭圆型也不是双曲型, 这与 KdV 方程的 Whitham 调制系统不同并且调制动力学在不同的单调区域更加丰富. 当 k_2>0 时, 谱特征值 \lambda _i 可以为复数, 方程 (1.4) 的 Whitham 调制系统是椭圆型的从而导致调制不稳定性[45]. 对于具有实数初值的聚焦 mKdV 方程, 初值问题的零色散极限中产生的调制方程是双曲型的的进而保证了调制系统的稳定性, 并使得色散冲击波的进一步研究成为可能[47,53]. 由于 Gardner 方程可以转化为聚焦 mKdV 方程[50], 我们将假设广义 Gardner 调制方程的双曲性来解决所研究的初始不连续问题. ...
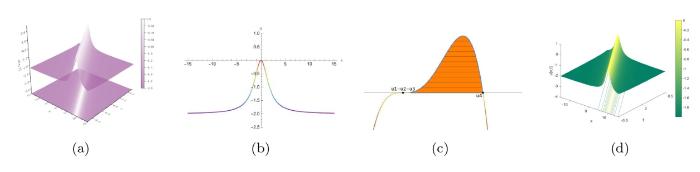
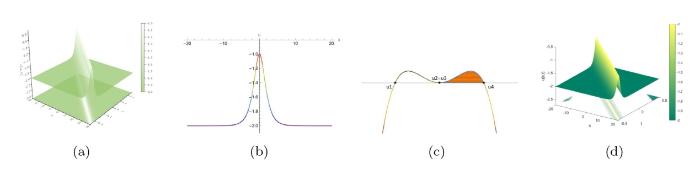
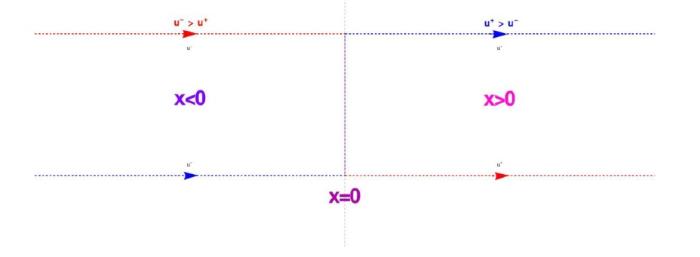
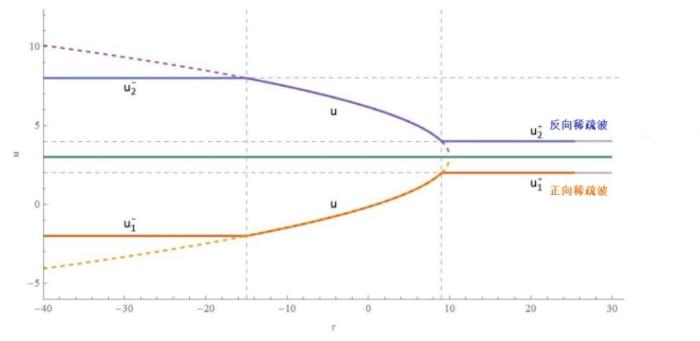
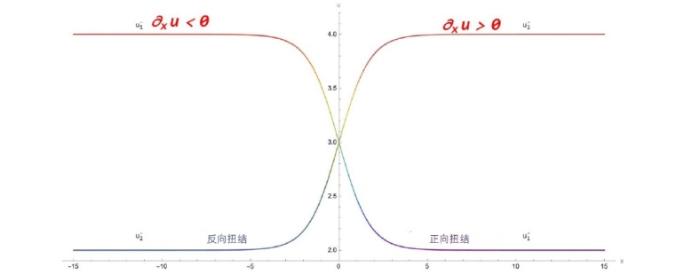
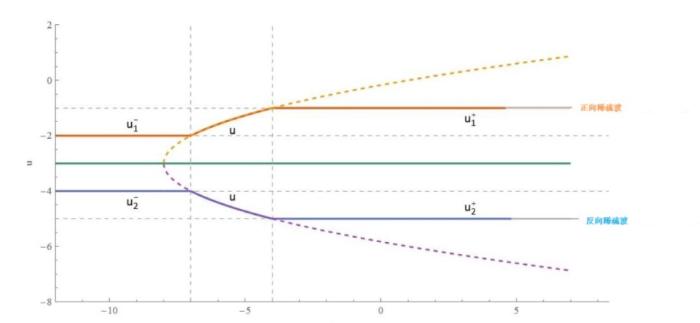
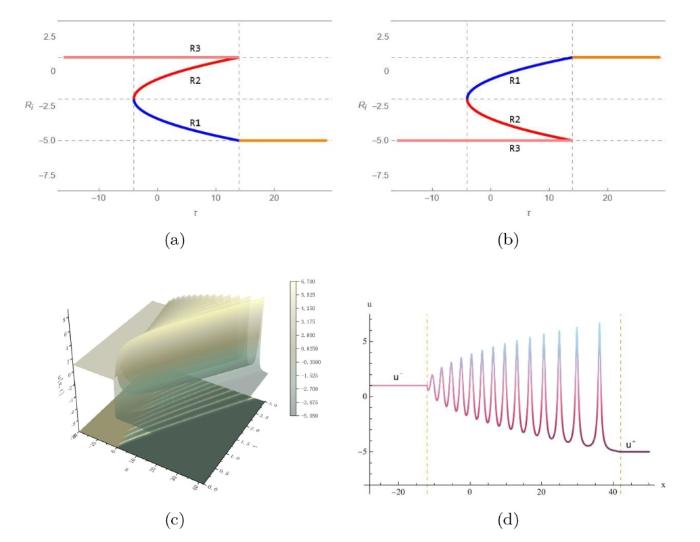
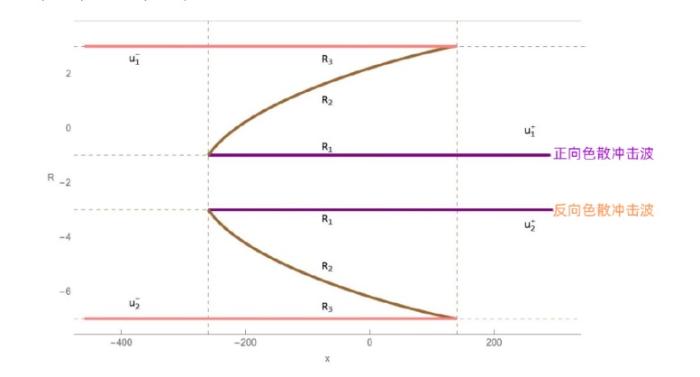
... 在研究 KdV 方程的过程中没有发现过三角色散冲击波的现象, 但在聚焦 mKdV 方程式和复数 mKdV 方程式中已经发现三角色散冲击波的一个边缘的振幅将逐渐消失而在另一个边缘的振幅存在非零有限值[47,48]. 与上一节中的色散冲击波, 稀疏波和扭结类似, 三角色散冲击波可以作为复合解的一部分来描述初始不连续性的演化, 并且也具有正向 \{ u^-\, TSW \rightarrowtail\,u^+\} 和反向 \{ u^-\,\leftarrowtail TSW \,u^+ \} 三角色散冲击波. ...
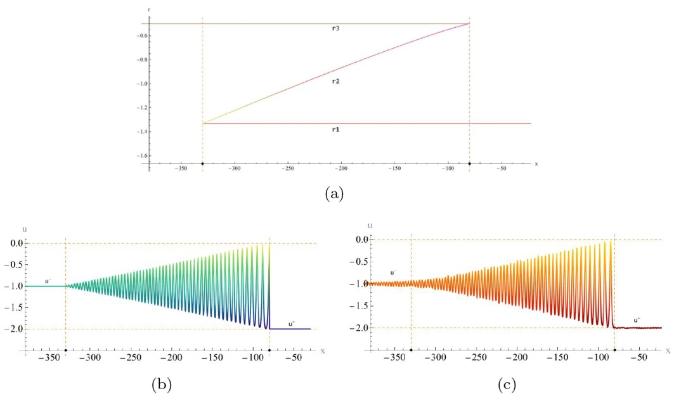
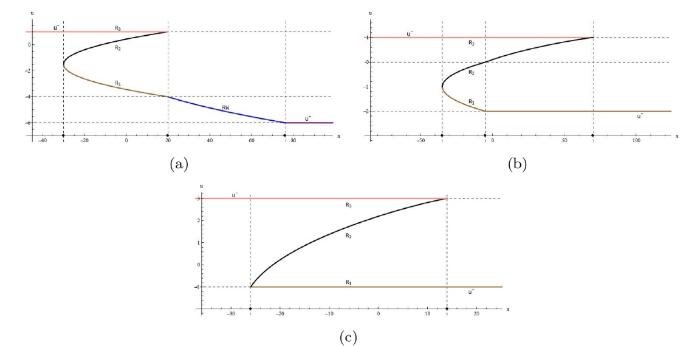
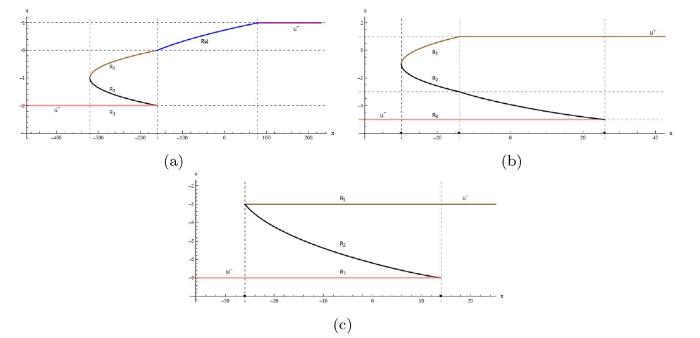
... 三角色散冲击波的黎曼不变量 r_1 和 r_2 在整个波列处处中相等从而导致 m 始终为 0, 从图32 中可以明显看到三角色散冲击波和色散冲击波复合解中的黎曼不变量 r_i 的演化行为的区别. 因此, 如果仍采用黎曼不变量 r_i 对解进行调制, 则它们不能像色散冲击波中的黎曼不变量一样满足 \tau =v_2\left( r_1,r_2,r^- \right) |_{r_1\ne r_2} 从而为初始条件 u^- 和 u^+ 提供必要的匹配. 由于任何黎曼不变量的函数仍然是黎曼不变量, 因此我们也可以采用另一种 Whitham 组合[47,50]. 根据方程 (4.6) 和 (4.5) 就可以得到正向与反向三角色散冲击波所对应的黎曼不变量 ...
On the Whitham equations for the defocusing complex modified KdV equation
2
2009
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
... 在研究 KdV 方程的过程中没有发现过三角色散冲击波的现象, 但在聚焦 mKdV 方程式和复数 mKdV 方程式中已经发现三角色散冲击波的一个边缘的振幅将逐渐消失而在另一个边缘的振幅存在非零有限值[47,48]. 与上一节中的色散冲击波, 稀疏波和扭结类似, 三角色散冲击波可以作为复合解的一部分来描述初始不连续性的演化, 并且也具有正向 \{ u^-\, TSW \rightarrowtail\,u^+\} 和反向 \{ u^-\,\leftarrowtail TSW \,u^+ \} 三角色散冲击波. ...
The extended Korteweg-de Vries equation and the resonant flow of a fluid over topography
1
1990
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
Undular bore theory for the Gardner equation
3
2012
... Whitham 将 KdV 方程的调制方程转换为黎曼对角形式, 从而将调制方程转换为三个一阶双曲偏微分方程的系统[33]. Gurevich 和 Pitaevskii 进一步利用 KdV 方程的调制方程推导出了色散冲击波解, 并且该方法可以推广到其他可积方程[39⇓⇓⇓-43]和不可积方程[44]. 在参考文献 [45] 中, mKdV 方程的调制系统通过平均守恒定律已经被得到, 并利用 Whitham 调制理论分析了振荡波列的稳定性. Kamchatnov 通过有限间隙积分方法推导了黎曼对角形式的离焦 mKdV 方程的调制系统, 由于调制方程总是双曲的, 因此可以得到稳定的周期解[46]. 然而, 聚焦 mKdV 方程的调制系统与 KdV 方程不同, 调制方程既可以是双曲型也可以是椭圆型, 就导致了调制系统为椭圆型时周期解的不稳定性. 聚焦 mKdV 方程的调制解包括一种不同于色散冲击波的三角色散冲击波 (TSW) 调制解, 这种情况下的 Whitham 调制方程其中的两个黎曼不变量不仅在后沿处相等, 而且在整个波列中处处相等, 这使得椭圆模量 m 始终为 0 . 三角色散冲击波作为复合解的一部分通常在初始条件满足特定情况时出现, 例如稀疏波 (RW) 与三角色散冲击波或色散冲击波与三角色散冲击波的复合波结构[47,48]. 由于 Gardner 方程是 KdV 和 mKdV 方程的组合, 当三次非线性系数的值很小时, Gardner 方程得到的色散冲击波解的性质与 KdV 方程的情况十分类似[49]. 参考文献 [50] 给出了 Gardner 方程的黎曼不变量形式的调制系统, 并且可以映射到 KdV 方程的调制系统中. ...
... 中是很明显的, 这是通过由 \psi(u) =\frac{1}{6}(k_2u^2+k_1u+d) 指定的映射 u\mapsto \psi 实现的. 当 u<-\frac{k_1}{2k_2} 或 u>-\frac{k_1}{2k_2} 时, \psi(u) 处于单调递增或单调递减区域. 广义 Gardner 方程的系统既不是椭圆型也不是双曲型, 这与 KdV 方程的 Whitham 调制系统不同并且调制动力学在不同的单调区域更加丰富. 当 k_2>0 时, 谱特征值 \lambda _i 可以为复数, 方程 (1.4) 的 Whitham 调制系统是椭圆型的从而导致调制不稳定性[45]. 对于具有实数初值的聚焦 mKdV 方程, 初值问题的零色散极限中产生的调制方程是双曲型的的进而保证了调制系统的稳定性, 并使得色散冲击波的进一步研究成为可能[47,53]. 由于 Gardner 方程可以转化为聚焦 mKdV 方程[50], 我们将假设广义 Gardner 调制方程的双曲性来解决所研究的初始不连续问题. ...
... 三角色散冲击波的黎曼不变量 r_1 和 r_2 在整个波列处处中相等从而导致 m 始终为 0, 从图32 中可以明显看到三角色散冲击波和色散冲击波复合解中的黎曼不变量 r_i 的演化行为的区别. 因此, 如果仍采用黎曼不变量 r_i 对解进行调制, 则它们不能像色散冲击波中的黎曼不变量一样满足 \tau =v_2\left( r_1,r_2,r^- \right) |_{r_1\ne r_2} 从而为初始条件 u^- 和 u^+ 提供必要的匹配. 由于任何黎曼不变量的函数仍然是黎曼不变量, 因此我们也可以采用另一种 Whitham 组合[47,50]. 根据方程 (4.6) 和 (4.5) 就可以得到正向与反向三角色散冲击波所对应的黎曼不变量 ...
30 years of finite-gap integration theory
1
2008
... 有限间隙积分方法是在与可积非线性色散方程有关的线性谱问题中获得周期或拟周期解的方法之一, 并在数学物理中的各种渐近问题中与势能递减的薛定谔算子具有重要的应用[51]. 当利用有限间隙积分方法得到的周期解或准周期解研究 Whitham 调制理论时, 如果准周期解的频谱带端点随 x 和 t 变化缓慢则可将其称为 Whitham 调制方程的黎曼不变量, 从而得到与线性光谱问题相关的可积方程的周期解所需的黎曼不变量参数化[42]. 广义 Gardner 方程对应的 Lax 对如下[26] ...
On the relationship between a 2\times2 matrix and second-order scalar spectral problems for integrable equations
1
2002
... \varPsi 必须满足相容性条件 \varPsi _{tx}=\varPsi _{xt} , 进而可以推导出零曲率方程 U_t-V_x+\left[ U,V \right] =0 , 其中 [U,V]=UV-VU . 我们可以通过下面的变换把矩阵形式的方程转换成期望的标量形式[52] ...
The zero-dispersion limit for the odd flows in the focusing Zakharov-Shabat hierarchy
1
2003
... 中是很明显的, 这是通过由 \psi(u) =\frac{1}{6}(k_2u^2+k_1u+d) 指定的映射 u\mapsto \psi 实现的. 当 u<-\frac{k_1}{2k_2} 或 u>-\frac{k_1}{2k_2} 时, \psi(u) 处于单调递增或单调递减区域. 广义 Gardner 方程的系统既不是椭圆型也不是双曲型, 这与 KdV 方程的 Whitham 调制系统不同并且调制动力学在不同的单调区域更加丰富. 当 k_2>0 时, 谱特征值 \lambda _i 可以为复数, 方程 (1.4) 的 Whitham 调制系统是椭圆型的从而导致调制不稳定性[45]. 对于具有实数初值的聚焦 mKdV 方程, 初值问题的零色散极限中产生的调制方程是双曲型的的进而保证了调制系统的稳定性, 并使得色散冲击波的进一步研究成为可能[47,53]. 由于 Gardner 方程可以转化为聚焦 mKdV 方程[50], 我们将假设广义 Gardner 调制方程的双曲性来解决所研究的初始不连续问题. ...
Numerical solution of the small dispersion limit of Korteweg-de Vries and Whitham equations
1
2007
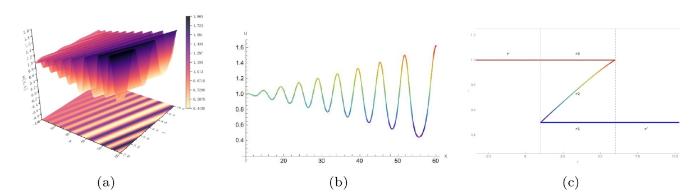
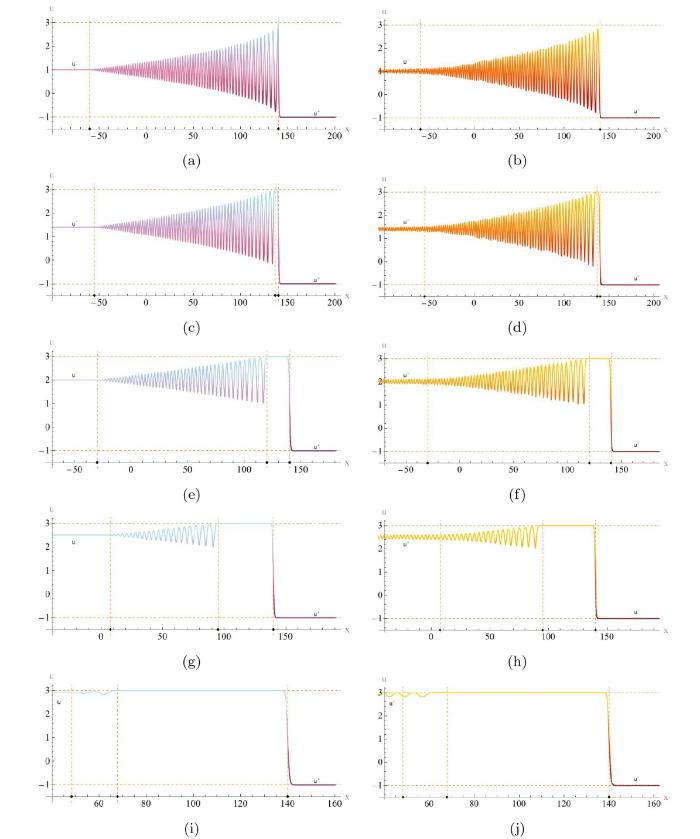
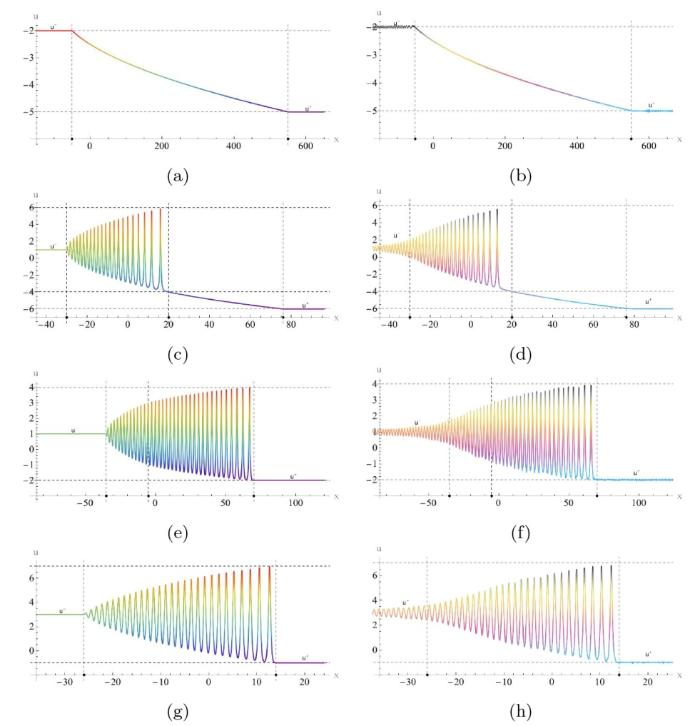
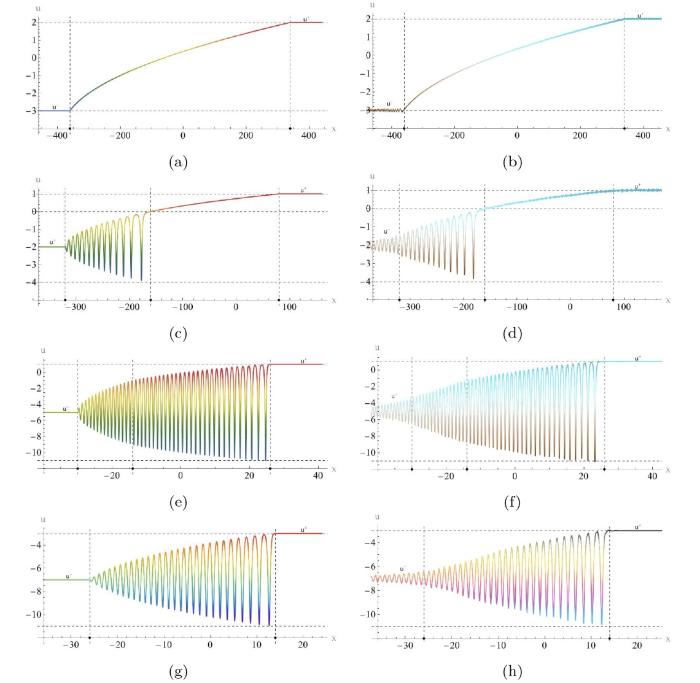
... 黎曼不变量的演化行为以及构建的解析解和数值模拟如图27 所示, 其中数值图中在后沿处延伸的小振幅振荡与 KdV 方程中观察到的现象一致[54,55]. ...
A numerical and theoretical study of certain nonlinear wave phenomena
1
1978
... 黎曼不变量的演化行为以及构建的解析解和数值模拟如图27 所示, 其中数值图中在后沿处延伸的小振幅振荡与 KdV 方程中观察到的现象一致[54,55]. ...