阶跃初值条件解的完全分类: 流体力学中广义 Gardner 方程的分析与数值验证

张岩,郝惠琴,郭睿

The Complete Classification of Solutions to the Step Initial Condition: Analysis and Numerical Verification for the Generalized Gardner Equation in Fluid Mechanics

Yan Zhang,Huiqin Hao,Rui Guo

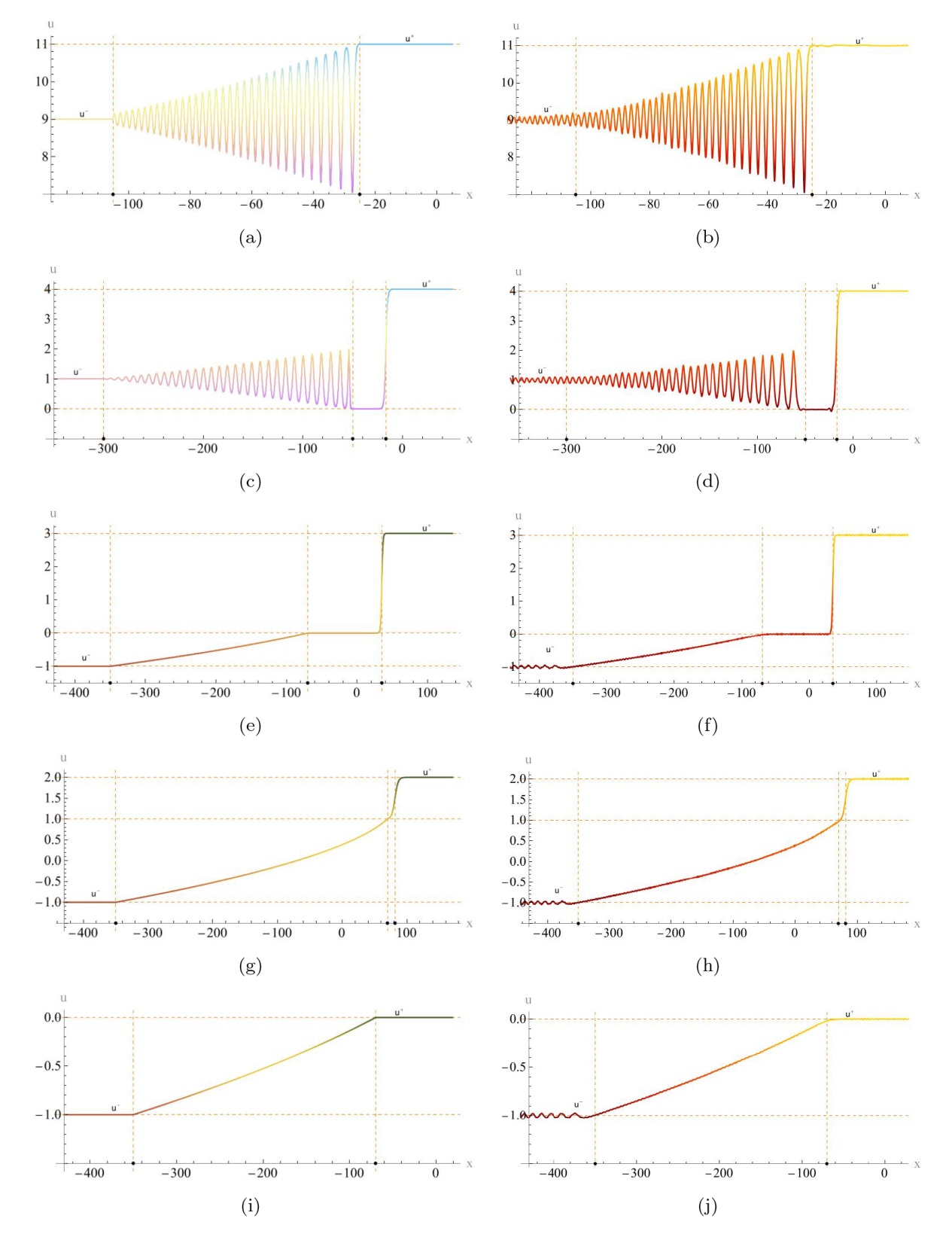
图30 方程 (1.4) 在区域 5 $ \sim $ 区域 8 中初始不连续的演化行为, 其中虚线分别代表边界 $ x^-=\tau ^-t $, $ x^+=\tau ^+t $ 和 $ x^*=\tau ^*t $. (a), (c), (e), (g) 和 (i) 为方程 (1.4) 的解析解. (b), (d), (f), (h) 和 (j) 为方程 (1.4) 的数值模拟结果, 参数如下: (a) $ k_1 =12 $, $ k_2 =-1 $, $ d =-30 $, $ u^- =9 $, $ u^+ =11 $, (c) $ k_1 =2 $, $ k_2 =-\frac{1}{2} $, $ d =-\frac{3}{2} $, $ u^- =1 $, $ u^+ =4 $, (e) $ k_1 =3 $, $ k_2 =-1 $, $ d =-1 $, $ u^- =-1 $, $ u^+ =3 $, (g) $ k_1 =3 $, $ k_2 =-1 $, $ d =-1 $, $ u^- =-1 $, $ u^+ =2 $, (i) $ k_1 =3 $, $ k_2 =-1 $, $ d =-1 $, $ u^- =-1 $, $ u^+ =0 $. 图中分别显示的是 $ t = 3, 100, 70, 70, 70 $ 时的情况.