1 引言
热传导反问题在航空航天, 机械工程, 冶金以及建筑消防等领域具有广泛的应用. 一般来说热传导反问题分为以下几类: 逆时热传导问题, 反边值问题, 反系数问题, 反边界问题及反源问题, 目前对于此类问题的研究已有一些重要进展. 在文献[1]中, 作者结合边界元和Tikhonov正则化方法研究了随时间变化的热传导方程反源问题. 文献[2]采用动力系统方法求解热传导方程的反问题, 并与Tikhonov正则化方法进行了比较. 文献[3]使用Tikhonov正则化和截断奇异值分解正则化方法, 研究了热传导方程的源项识别问题, 利用确定位置的测量数据反演未知热源强度. 在文献[4]中, 作者比较了两种求解热传导方程初始值反问题的数值方法. 文献[5]研究了通过圆盘上终值时刻的温度场观测数据来反演初始温度的逆问题, 得到了初始数据和观测数据之间的积分表示关系. 文献[6]作者利用Landweber迭代正则化方法研究了热传导方程反源问题, 在最优控制框架的基础上, 得到了目标函数最小化的必要条件. 文献[7]中, 作者利用谱配置方法与正则化技术相结合的数值方法求解了四分之一平面内热传导反问题. 文献[8]研究了二维逆时热传导反问题的改进正则化方法, 得到了H
该文主要研究一类三维矩形截面梁结构热传导反问题的数值算法, 此问题源于建筑物梁结构受热问题的研究. 我们分析了规则区域上的三维热传导反问题, 利用分离变量方法建立任意时刻温度场与初始温度场之间的对应关系, 给出明确的反演公式. 为了避免“逆问题犯罪”有效求解反问题, 对于正问题求解本文使用有限元对空间离散, 借助有限差分法对时间离散, 简要给出了热传导问题的数值计算方法, 对不同时刻节点处的温度进行数值求解. 针对数值求解反演方程的不适定性, 我们分别采用了Tikhonov正则化和终值数据扰动正则化方法反演初始温度场, 并从数值上分析了正则化参数以及数据观测时间对反演结果的影响. 结论表明, 随着时间推移温度场逐渐衰减, 此时噪声数据(误差水平)带来的影响逐渐增大, 反演效果逐渐变差, 甚至完全得不到初始温度场, 这种反演结果和实际物理过程一致. 论文结构如下: 第2, 3节给出三维热传导正问题的有限元解法及数值实验; 第4节中研究三维逆时热传导问题, 证明了反问题局部稳定性, 第5节给出了反问题求解的两种数值方法, 并通过数值结果验证了算法的有效性, 最后在第6节中给出了总结.
2 热传导正问题
其中
初始条件为
边界条件为
其中
该文所研究的正问题是已知初始条件, 边界条件以及相关物理参数, 求不同时刻空间
其中
利用高斯公式得
这里
利用公式(2.4), (2.6)和(2.7), 将(2.5)式转化为
其中
由(2.9)式可得, 温度梯度矩阵为
考虑到
其中
其中
和
上述方程仅在空间中离散, 还需要对时间项进行离散, 这里使用有限差分法. 将
引入参数
将(2.12)式离散后得
整理得到全离散格式
3 数值实验
给定三维空间中的一个正方体
表 1
当
| T | J=10 | J=20 | |||||
| 2 | 0.0972 | 0.0087 | 0.0111 | 0.0961 | 0.0030 | 0.0039 | |
| 4 | 0.1537 | 0.0137 | 0.0222 | 0.1514 | 0.0048 | 0.0077 | |
| 6 | 0.1824 | 0.0163 | 0.0335 | 0.1790 | 0.0057 | 0.0116 | |
| 8 | 0.1923 | 0.0172 | 0.0449 | 0.1881 | 0.0059 | 0.0155 | |
| T | J=30 | J=40 | |||||
| 2 | 0.0961 | 0.0030 | 0.0039 | 0.1435 | 0.0016 | 0.0020 | |
| 4 | 0.1514 | 0.0048 | 0.0077 | 0.2260 | 0.0025 | 0.0041 | |
| 6 | 0.1790 | 0.0057 | 0.0116 | 0.2669 | 0.0030 | 0.0061 | |
| 8 | 0.1881 | 0.0059 | 0.0155 | 0.2803 | 0.0031 | 0.0082 | |
图 1
图 1
(a)、(b)、(c)、(d)图分别为正问题在
4 三维热传导反问题
产生的逆时问题. 利用
利用分离变量法, 可得
其中核函数为
为证明反问题的条件稳定性, 我们令
这里常数
这里的
令
该问题的解可用
这里常数
定义
定理4.1 对于
证 类似(4.8)式可得
这里常数
通过Parserval不等式和
对于
由于
由定理4.1, 我们得到了反问题的条件稳定性.
定理4.2 对于
成立.
证 容易验证, 当
5 反问题数值求解
本节主要采用两种正则化方法对第4节的逆时热传导问题进行数值求解.
方法一 Tikhonov正则化方法[19].
公式(4.3)建立了不同时刻温度场和
其中
方法二 终值数据扰动的正则化方法.
对于给定的
对精确的输入数据来讨论近似解
其中
由(5.3)式得
注意到
得
这是一个关于
对于右端项加上一定的扰动, 可进一步估计收敛速度[17].
先考虑Tikhonov正则化方法. 给定初始温度
表 2
当
| δ | α = 0.0001 | α = 0.0005 | |||||
| 0.001 | 0.3704 | 0.0119 | 0.0117 | 0.3165 | 0.0100 | 0.0100 | |
| 0.005 | 0.4378 | 0.0134 | 0.0138 | 0.3815 | 0.0126 | 0.0121 | |
| 0.01 | 0.5333 | 0.0198 | 0.0169 | 0.4628 | 0.0156 | 0.0146 | |
| 0.05 | 1.3499 | 0.0734 | 0.0427 | 1.1337 | 0.0432 | 0.0359 | |
| δ | α = 0.001 | α = 0.005 | |||||
| 0.001 | 0.2490 | 0.0080 | 0.0079 | 0.2778 | 0.0088 | 0.0088 | |
| 0.005 | 0.3122 | 0.0100 | 0.0099 | 0.2147 | 0.0068 | 0.0068 | |
| 0.01 | 0.3950 | 0.0122 | 0.0125 | 0.1381 | 0.0048 | 0.0044 | |
| 0.05 | 1.0394 | 0.0332 | 0.0329 | 0.5074 | 0.0152 | 0.0160 | |
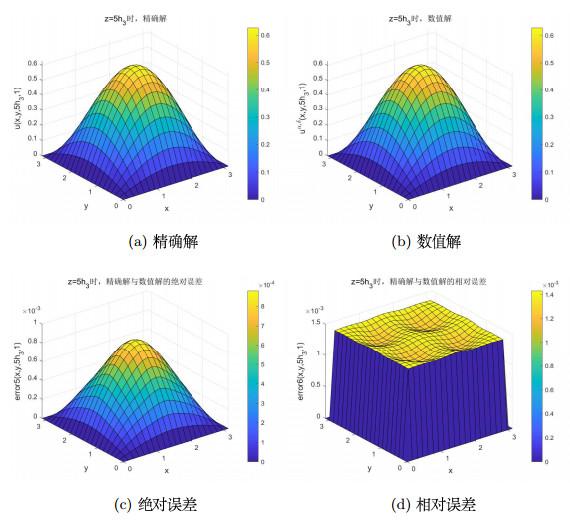
图 2
图 2
(a)、(b)、(c)、(d)图分别为反问题在
下面我们考虑终值数据扰动的正则化方法. 给定初始温度
反演
表 3
当
| α | T=4 | T=6 | |||||
| 0.0001 | 0.2490 | 0.0080 | 0.0079 | 0.2778 | 0.0088 | 0.0088 | |
| 0.0005 | 0.3122 | 0.0100 | 0.0099 | 0.2147 | 0.0068 | 0.0068 | |
| 0.001 | 0.3950 | 0.0122 | 0.0125 | 0.1381 | 0.0048 | 0.0044 | |
| 0.005 | 1.0394 | 0.0332 | 0.0329 | 0.0377 | 0.0011 | 0.0013 | |
| α | T=8 | T=10 | |||||
| 0.0001 | 0.4306 | 0.0141 | 0.0154 | 0.5406 | 0.0201 | 0.0193 | |
| 0.0005 | 0.3987 | 0.0130 | 0.0142 | 0.4987 | 0.0159 | 0.0178 | |
| 0.001 | 0.3616 | 0.0117 | 0.0129 | 0.4513 | 0.0142 | 0.0161 | |
| 0.005 | 0.0686 | 0.0023 | 0.0024 | 0.0789 | 0.0024 | 0.0028 | |
| α | T=20 | T=30 | |||||
| 0.0001 | 1.0701 | 0.0332 | 0.0382 | 1.5610 | 0.0492 | 0.0557 | |
| 0.0005 | 0.9424 | 0.0297 | 0.0336 | 1.1354 | 0.0359 | 0.0405 | |
| 0.001 | 0.7844 | 0.0247 | 0.0280 | 0.6202 | 0.0196 | 0.0221 | |
| 0.005 | 0.4205 | 0.0133 | 0.0150 | 2.9273 | 0.0926 | 0.1044 | |
| α | T=40 | T=50 | |||||
| 0.0001 | 1.8839 | 0.0595 | 0.0672 | 1.6395 | 0.0519 | 0.0585 | |
| 0.0005 | 0.5125 | 0.0162 | 0.0183 | 2.3469 | 0.0742 | 0.0837 | |
| 0.001 | 1.0346 | 0.0327 | 0.0369 | 6.0408 | 0.1910 | 0.2154 | |
| 0.005 | 9.2018 | 0.2910 | 0.3281 | 17.8107 | 0.5632 | 0.6350 | |
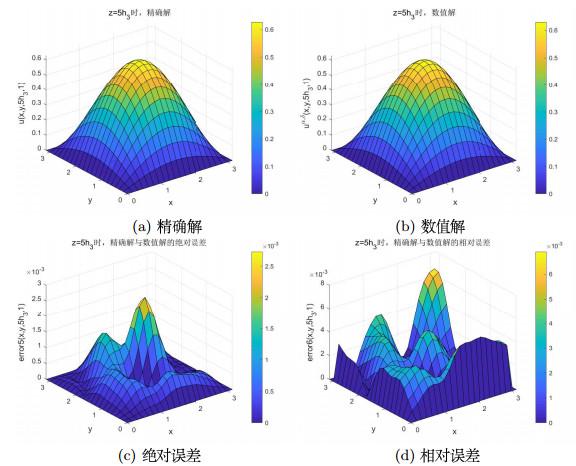
图 3
图 3
(a)、(b)、(c)、(d)图分别为反问题在
表 4
当
| α | T=4 | T=6 | |||||
| 0.0001 | 0.6014 | 0.0454 | 0.0214 | 0.9492 | 0.0748 | 0.0338 | |
| 0.0005 | 0.2497 | 0.0135 | 0.0089 | 0.3730 | 0.0185 | 0.0133 | |
| 0.001 | 0.2042 | 0.0101 | 0.0073 | 0.3015 | 0.0144 | 0.0108 | |
| 0.005 | 0.0210 | 0.0015 | 0.0007 | 0.0585 | 0.0031 | 0.0021 | |
| α | T=8 | T=10 | |||||
| 0.0001 | 1.0726 | 0.0650 | 0.0382 | 1.1132 | 0.0726 | 0.0397 | |
| 0.0005 | 0.4502 | 0.0205 | 0.0161 | 0.5333 | 0.0230 | 0.0190 | |
| 0.001 | 0.3932 | 0.0199 | 0.0140 | 0.4762 | 0.0163 | 0.0170 | |
| 0.005 | 0.0865 | 0.0044 | 0.0031 | 0.0953 | 0.0037 | 0.0034 | |
| α | T=20 | T=30 | |||||
| 0.0001 | 1.1529 | 0.0486 | 0.0411 | 1.5826 | 0.0521 | 0.0564 | |
| 0.0005 | 0.9618 | 0.0333 | 0.0343 | 1.1500 | 0.0356 | 0.0401 | |
| 0.001 | 0.7997 | 0.0240 | 0.0285 | 0.6346 | 0.0203 | 0.0226 | |
| 0.005 | 0.4066 | 0.0131 | 0.0145 | 2.9149 | 0.0922 | 0.1039 | |
| α | T=40 | T=50 | |||||
| 0.0001 | 1.8994 | 0.0617 | 0.0677 | 1.6546 | 0.0525 | 0.0590 | |
| 0.0005 | 0.5265 | 0.0166 | 0.0188 | 2.3341 | 0.0738 | 0.0832 | |
| 0.001 | 1.0211 | 0.0325 | 0.0364 | 6.0298 | 0.1907 | 0.2150 | |
| 0.005 | 9.1925 | 0.2907 | 0.3278 | 17.8057 | 0.5631 | 0.6349 | |
图 4
图 4
(a)、(b)、(c)、(d)图分别为反问题在
6 结论
本文研究了在数学物理和工程领域中有重要应用的一类三维逆时热传导问题. 基于变分法和有限元对正问题进行了数值求解. 进一步在规则区域内使用分离变量法构造了两个反演算法, 并在一定假设条件下证明了反问题的局部稳定性. 通过数值实验验证了算法的有效性, 并分析了不同参数对反演结果的影响. 本文得到的理论和算法丰富了目前关于三维逆时热传导问题的研究结果. 文中的反演算法针对第一类和第二类边界条件都是可以适用的, 但对于一般的第三类边界条件, 由于不能直接建立分离变量形式的反演公式, 需要尝试使用其它数学理论和方法加以解决. 针对第三类边界条件的三维逆时问题, 我们将在后续的研究中继续考虑其稳定高效的反演方法.
参考文献
An inverse time-dependent source problem for the heat equation
DOI:10.1016/j.apnum.2013.02.004 [本文引用: 1]
Dynamic system method for solving inverse problems in heat conduction equations
Source strength identification problem for the three-dimensional inverse heat conduction equations
DOI:10.1080/17415977.2019.1665663 [本文引用: 1]
A comparison of some inverse methods for estimating the initial condition of the heat equation
DOI:10.1016/S0377-0427(98)00249-0 [本文引用: 1]
Initial inverse problem in heat equation with Bessel operator
DOI:10.1016/S0017-9310(02)00019-4 [本文引用: 1]
Reversing inverse problem of source term of heat conduction equation
DOI:10.12677/AAM.2019.81012 [本文引用: 1]
Numerical investigation of an inverse problem based on regularization method
DOI:10.1007/s40096-019-0288-2 [本文引用: 1]
An improved regularization method for initial inverse problem in 2-D heat equation
DOI:10.1016/j.apm.2014.05.014 [本文引用: 1]
Nonlinear inverse heat conduction problem of surface temperature estimation by calibration integral equation method
DOI:10.1080/10407790.2018.1464316 [本文引用: 1]
Nonlinear unsteady inverse boundary problem for heat conduction equation
DOI:10.1515/aoter-2017-0011 [本文引用: 1]
On the non-linear integral equation approach for an inverse boundary value problem for the heat equation
Generalized Tikhonov methods for an inverse source problem of the time-fractional diffusion equation
Moving boundary identification for a two-dimensional inverse heat conduction problem
DOI:10.1080/17415977.2011.603084 [本文引用: 1]
Inverse problems for partial differential equations
DOI:10.4171/OWR/2012/11 [本文引用: 1]
Numerical solution of forward and backward problem for 2-D heat conduction equation
DOI:10.1016/S0377-0427(01)00595-7 [本文引用: 2]