1 引言
应用贝叶斯方法进行统计推断主要取决于"先验分布"和"损失函数"两个方面.一个方面,先验分布经常取决于超参数,在这种情况下我们经常使用多层贝叶斯方法(hierarchical Bayesian method);另一个方面,损失函数在贝叶斯统计推断中也非常重要,最常用的是平方损失函数下的贝叶斯估计.当然,还有一些损失函数在贝叶斯统计推断中也很重要,例如, LINEX损失函数,熵损失函数,加权平方损失函数等. Ali等在文献[1]中,根据不同的损失函数(包括:平方损失,加权平方损失,预防损失,熵损失和K-损失等),用贝叶斯方法推导Lindley分布的性质(包括:贝叶斯估计、后验风险等).
很多实际问题可以用Poisson分布来描述,例如,可以用Poisson分布来描述在一定时间内稀有事件发生的次数等.对Poisson分布的研究具有重要的理论和实际应用价值.在文献[11]中,对Poisson分布的参数,讨论了极大似然估计、矩估计以及Bayes估计之间的关系,并对优劣性进行了分析.在文献[12]和[13]中,对Poisson分布的参数,分别在
本文在文献[14]的基础上,对Poisson分布参数的E-Bayes估计及其E-MSE进行了讨论.本文在第二节中,基于E-Bayes估计,引入了E-Bayes估计的E-MSE的定义;在第三节中,讨论了在不同损失函数下参数的Bayes估计;在第四节中,在不同损失函数下给出了Poisson分布参数的E-Bayes估计;在第五节中,在不同损失函数下给出了参数E-Bayes估计的E-MSE的表达式;在第六节中,给出模拟算例;在第七节中,给出应用实例.
2 E-Bayes估计及其E-MSE的定义
设随机变量
设
其中
如果取
其中
根据文献[15],超参数
注意到
对
在文献[14]中给出了参数的E-Bayes估计的定义,现在叙述在如下的定义2.1中.
定义2.1 对
是参数
从定义2.1可以看出,参数
是参数
提出一种参数估计方法,一般要给出估计的误差.通常用MSE (mean square error)来度量估计的误差. E-Bayes估计法提出的时间不长,其研究成果也不多.以前E-Bayes估计误差的分析表达式一直没有被研究,最近Han在文献[17]中提出了E-MSE (expected mean square error)的定义,并用它来研究E-Bayes估计的误差.关于E-MSE的定义,现在叙述如下.
定义2.2 对
是
从定义2.2可以看出,
是
3 不同损失函数下参数的Bayes估计
损失函数在贝叶斯统计推断中是非常重要的,最常用的是平方损失函数下的贝叶斯估计.根据文献[1],有如下引理3.1.
引理3.1 设
(ⅰ)在平方损失函数
(ⅱ)在K -损失函数
(ⅲ)在加权平方损失函数
这里
4 不同损失函数下λ
定理4.1 设
给出,在不同损失函数下,有以下结论:
(ⅰ)在平方损失函数下,
(ⅱ)在K-损失函数下,
(ⅲ)在加权平方损失函数下,
其中
证 (ⅰ)的证明已在文献[14]中给出了,这里从略.
(ⅱ)设
因此
根据引理3.1的(ⅱ),在K -损失函数下,
若超参数
(ⅲ)根据(ⅱ)的证明过程,有
若超参数
证毕.
5 不同损失函数下ˆλEBi (i=1,2,3)
定理5.1 设
(ⅰ)在平方损失函数下,
(ⅱ)在K -损失函数下,
(ⅲ)在加权平方损失函数下,
其中
证 (ⅰ)根据定理4.1的(ⅱ)的证明过程,
若超参数
(ⅱ)根据定理4.1的(ⅱ)的证明过程,
根据定理4.1的(ⅱ),在K-损失函数下,
若超参数
(ⅲ)根据(ⅱ)的证明过程,有
若超参数
证毕.
6 模拟算例
表 1
| 20 | 40 | 60 | 80 | 100 | |
| 0.5074 | 0.5057 | 0.5049 | 0.5022 | 0.5015 | |
| 0.4873 | 0.4932 | 0.4966 | 0.4960 | 0.4964 | |
| 0.4636 | 0.4810 | 0.4884 | 0.4898 | 0.4915 | |
| E-MSE | 0.0250 | 0.0125 | 0.0083 | 0.0062 | 0.0048 |
| E-MSE | 0.0256 | 0.0126 | 0.0084 | 0.0063 | 0.0050 |
| E-MSE | 0.0274 | 0.0131 | 0.0086 | 0.0064 | 0.0051 |
表 2
| 20 | 40 | 60 | 80 | 100 | |
| 0.9977 | 1.0003 | 0.9988 | 0.9997 | 0.9999 | |
| 0.9730 | 0.9879 | 0.9905 | 0.9936 | 0.9947 | |
| 0.9489 | 0.9756 | 0.9823 | 0.9874 | 0.9898 | |
| E-MSE | 0.0487 | 0.0247 | 0.0165 | 0.0124 | 0.0099 |
| E-MSE | 0.0493 | 0.0249 | 0.0166 | 0.0125 | 0.0100 |
| E-MSE | 0.0511 | 0.0253 | 0.0168 | 0.0126 | 0.0101 |
表 3
| 20 | 40 | 60 | 80 | 100 | |
| 1.9735 | 1.9882 | 1.9929 | 1.9936 | 1.9941 | |
| 1.9489 | 1.9758 | 1.9846 | 1.9873 | 1.9891 | |
| 1.9247 | 1.9635 | 1.9764 | 1.9811 | 1.9841 | |
| E-MSE | 0.0963 | 0.0491 | 0.0329 | 0.0247 | 0.0197 |
| E-MSE | 0.0969 | 0.0492 | 0.0330 | 0.0248 | 0.0198 |
| E-MSE | 0.0987 | 0.0497 | 0.0332 | 0.0249 | 0.0199 |
表 4
| 20 | 40 | 60 | 80 | 100 | |
| 3.9248 | 3.9617 | 3.9720 | 3.9787 | 3.9885 | |
| 3.9003 | 3.9493 | 3.9638 | 3.9725 | 3.9886 | |
| 3.8760 | 3.9370 | 3.9555 | 3.9663 | 3.9887 | |
| E-MSE | 0.1915 | 0.0978 | 0.0656 | 0.0494 | 0.0395 |
| E-MSE | 0.1921 | 0.0980 | 0.0657 | 0.0495 | 0.0397 |
| E-MSE | 0.1939 | 0.0984 | 0.0659 | 0.0496 | 0.0398 |
因此如果以"E-MSE"作为评价标准,在E-MSE越小越优的意义下,
7 应用实例
表 6
| 1 | 3 | 5 | 7 | 9 | 极差 | |
| 2.8225089 | 2.8197148 | 2.8169281 | 2.8141487 | 2.8113765 | 0.0111324 | |
| 2.8220131 | 2.8192195 | 2.8164332 | 2.8136543 | 2.8108827 | 0.0111304 | |
| 2.8215173 | 2.8187242 | 2.8159385 | 2.8131600 | 2.8103889 | 0.0111284 | |
| E-MSE | 0.0027987 | 0.0027932 | 0.0027877 | 0.0027822 | 0.0027767 | 2.20e-005 |
| E-MSE | 0.0027990 | 0.0027934 | 0.0027879 | 0.0027824 | 0.0027769 | 2.21e-005 |
| E-MSE | 0.0027997 | 0.0027942 | 0.0027886 | 0.0027832 | 0.0027777 | 2.20e-005 |
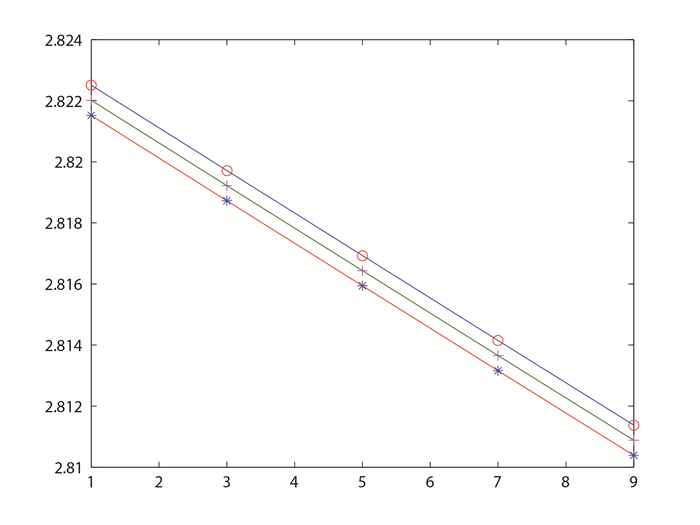
图 1
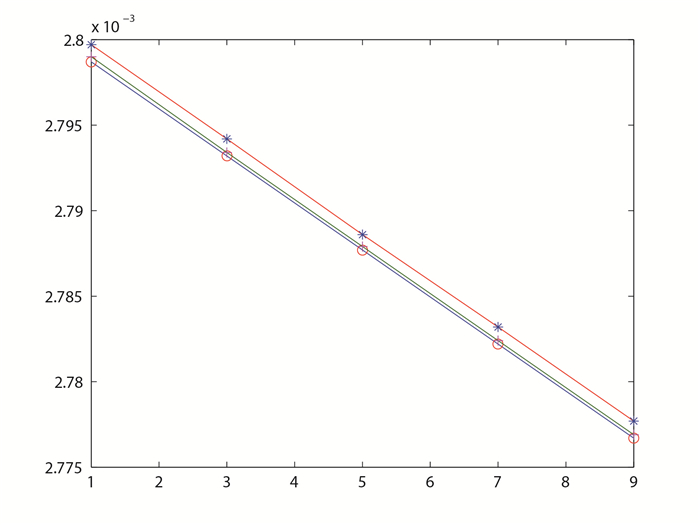
图 2
从表 6、图 1和图 2可以看出,对不同的
由于对不同的
8 结论
本文在文献[14]的基础上,基于E-Bayes估计的定义(见定义2.1),引入了E-Bayes估计的E-MSE (expected mean square error)的定义(见定义2.2).在三个不同损失函数下,对Poisson分布的参数分别给出了E-Bayes估计(见定理4.1)及其E-MSE (见定理5.1).
回顾模拟算例和应用实例,我们发现有如下结论:
(1)不同的损失函数对
(2)对E-MSE
(3)如果以E-MSE作为评价标准,在E-MSE越小越优的意义下,
参考文献
A study of the effect of the loss function on Bayes estimate, posterior risk and hazard function for Lindley distribution
DOI:10.1016/j.apm.2012.12.008 [本文引用: 2]
Hierarchical Bayesian analysis of the seemingly unrelated regression and simultaneous equations models using a combination of direct monte carlo and importance sampling techniques
DOI:10.1214/10-BA503 [本文引用: 1]
Hierarchical Bayesian modeling of the space-time diffusion patterns of cholera epidemic in Kumasi, Ghana
DOI:10.1111/j.1467-9574.2010.00475.x
E-Bayesian estimation and hierarchical Bayesian estimation of failure rate
DOI:10.1016/j.apm.2008.03.019 [本文引用: 1]
E-Bayesian estimation of the reliability derived from binomial distribution
The E-Bayesian and hierarchical Bayesian estimations of Pareto distribution parameter under different loss functions
DOI:10.1080/00949655.2016.1221408
E-Bayesian estimation for the Burr type XⅡ model based on type-2 censoring
E-Bayesian estimation for the geometric model based on record statistics
E-Bayesian and hierarchical Bayesian estimations for the system reliability parameter based on asymmetric loss function
DOI:10.1080/03610926.2014.968736 [本文引用: 1]
Poisson分布参数的几种估计
DOI:10.3969/j.issn.1009-6051.2003.06.007 [本文引用: 1]
Several estimates of Poisson distribution parameter
DOI:10.3969/j.issn.1009-6051.2003.06.007 [本文引用: 1]
Q-对称熵损失下Poisson分布参数倒数的估计
DOI:10.3969/j.issn.1002-8743.2007.02.008 [本文引用: 1]
The estimation of reciprocal of distribution parameters for Poisson distribution under Q-symmetric loss function
DOI:10.3969/j.issn.1002-8743.2007.02.008 [本文引用: 1]
Poisson分布参数的E-Bayes估计及其性质
The E-Bayesian estimation of the parameter for Poisson distribution and its properties
多层先验分布的构造及其应用
The structure of hierarchical prior distribution and its applications