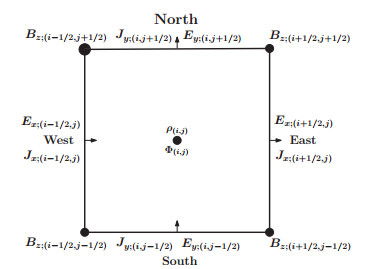
1 引言
这里的符号取它们通常表示的物理含义.描述一种无碰撞等离子的Vlasov方程为
这里
这里
那么这两个散度方程就一直成立,电磁场动力学问题仅需求解Maxwell方程组的前两个旋度方程即可.但是电流连续性方程(1.5)在离散情况下却不一定成立,电磁场量、电荷密度和电流密度定义在空间网格上,带电粒子可以取任意位置.采用某种分配方案,从带电粒子的运动信息得到的电荷密度和电流密度不一定满足离散电流连续性方程.本文关注满足电荷守恒的电流分配方案,即能够使得网格上的电荷和电流密度满足离散电流连续性方程的分配方案.
图 1
对于指标为
当采用FDTD方法求解电磁场时,有三种常用的满足电荷守恒的电流分配方案[16-18].具体地, Villasenor等[16]假设一个电荷分布为常数的宏粒子在一个时间步内沿直线运动,任何被宏粒子所扫略过的元胞边界都会有一个电流通过.该方法在本文被称为“V方法”. Esirkepov等[17]假设一个带有任意阶电荷分布的宏粒子在一个时间步内沿直线运动,同时给出了电流密度的一个特别的定义:电流密度的每一个分量都是几个“形因子(form-factor)”差的唯一线性组合.该方法在本文被称为“E方法”. Umeda等[18]假定宏粒子在一个时间步内的运动轨迹是一条由两个直的子线段所组成的折线.网格上的电流密度由每一小段轨迹所对应的电荷运动通量相加得到.该方法在本文被称为“U方法”.基于这些方法, Barthelme[19], Yu[20]等人提出了基于更高阶形状函数的、满足电荷守恒的电流分配方案.
本文针对一个带有常数电荷分布的宏粒子在二维、三维Yee网格上移动所涉及的、电荷守恒的电流分配方案,用求解线性代数方程组的方式得出通用公式.对于Yee网格上的某一个元胞,当有电流从元胞边界流进或流出时,元胞内的电量会发生变化.因此,我们只关注那些在宏粒子运动前后电荷量发生变化的元胞及定义在这些元胞边界上的电流.当这些元胞及其内部电荷变化量被确定了之后,根据电荷守恒定律就能够建立起一个以所有元胞边界上电流密度为变量的线性代数方程组.求得线性代数方程组的一个解,即得到一种电流密度分配方案.求得线性代数方程组所有的解,即得到所有的电流密度分配方案.在二维Yee网格上,带有常数电荷分布的宏粒子在一个时间内的运动可能会涉及四个、六个或七个元胞共三种情形.针对每一种情形,本文列出并求解所对应的线性代数方程组,同时将V方法, E方法和U方法作为其特解详细分析.在三维Yee网格中,带有常数电荷分布的宏粒子在一个时间内的运动可能会涉及不同数目的元胞共八种情形,详见文献[18].本文将针对一种最常见、最简单涉及八个元胞的情形,作同样的分析.
2 形状函数和形因子
在EMPIC模拟中,并不追踪所有的带电粒子,而是用相空间中
其中,
在早期的模拟中,并没有赋予宏粒子形状和大小,函数
研究成果[3]发现为每一个宏粒子(所带电荷)赋予一个有限大小和具体的形状,可以大大减小宏粒子的近距离相互作用、提高计算精度,这里用形状函数
接下来继续介绍一个在EMPIC中经常用到的概念:形因子,用函数
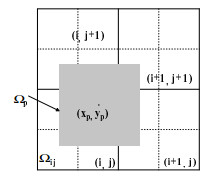
图 2
在任意一个元胞上对宏粒子的形状函数做积分,可以得到宏粒子相应于该元胞的形因子.假设图 2中宏粒子的带电量为
其中
表 1列出了几个典型而常用的一维形状函数和形因子,通过张量积运算可以将它们自然推广至高维.
表 1 一维典型形状函数与形因子
3 电荷守恒电流分配方案的统一公式(二维)
带有一定形状和大小的宏粒子在网格上移动,会引起网格上某些元胞内的电量发生变化.将宏粒子在一个时间内运动前后所涉及的元胞集合记为
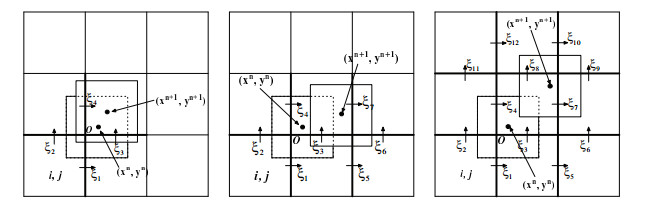
带有一阶形状函数的宏粒子在二维Yee网格上移动一个时间步,可能会引起四个、六个或七个元胞内的电荷量发生变化. 图 3是一个示意图,最左边的图是涉及四个元胞的情况,
图 3
3.1 四个元胞
在涉及四个元胞时,相关形因子见附录表.
3.1.1 V、E、U方法参数计算
下面验证V方法、E方法和U方法给出的公式分别是通解公式(3.1)的三个特解.在四个元胞情形下, V方法、E方法和U方法给出的公式列在表 2中.
当参数
表 2 在四个元胞情形下, V方法、E方法和U方法给出的电流密度公式
| V method | E method | U method | |
| 其中: | |||
3.2 六个元胞
在涉及六个元胞时,相关形因子见附录表 2.
3.2.1 V、E、U方法参数计算
下面验证V方法、E方法和U方法给出的公式分别是通解公式(3.2)的三个特解.在六个元胞情形下, V方法、E方法和U方法给出的公式列在表 3中.
表 3 在六个元胞情形下, V方法、E方法和U方法给出的电流密度公式
| V method | E method | U method | |
| 其中: | |||
当参数
当参数
当参数
3.3 七个元胞
在涉及七个元胞时,相关形因子见附录表 3.注意这里,宏粒子在运动前后涉及的元胞集合为
是解空间的四个基向量.
3.3.1 V、E、U方法参数计算
下面验证V方法、E方法和U方法给出的公式分别是通解公式(3.3)的三个特解.在七个元胞情形下, V方法、E方法和U方法给出的公式列在表 4中.
表 4 在七个元胞情形下, V方法, E方法和U方法给出的电流密度公式
| V method | E method | U method | |
| 其中: | |||
当参数
时,有
当参数
时,有
当参数
时,有
4 电荷守恒电流分配方案的统一公式(三维)
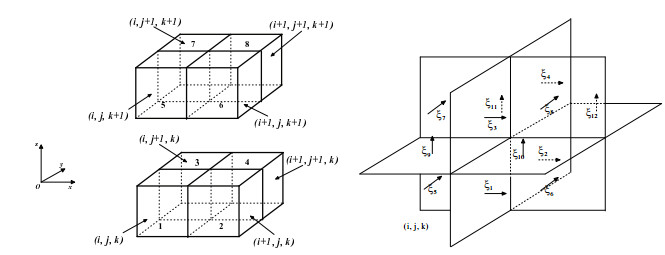
图 4
在该情形下,相关形因子见附录表 4,
其中
是解空间的基向量,
具体写出通解的表达式为
上面已经给出了一种最常见、最简单的情形下,电流密度的通用公式.其他情形下电流密度的通用公式可以用同样的方法给出.下面给出V方法和E方法的公式,找出相应于通解(4.1)的参数.这里不再列出U方法,因为经过仔细推导发现, U方法给出的三维公式不再满足电荷守恒(具体推导见附录).
4.1 V、E方法参数计算
在该情形下, V方法给出的公式为
其中,
在该情形下, E方法给出的公式为
5 结论
本文从代数角度提出了一个EMPIC模拟中、适用于Yee网格的、电荷守恒的电流分配方案所满足的统一公式.这个公式是通过求解建立在电荷守恒定律上的线性代数方程组而得到的.一个带有一阶形状函数的宏粒子单位时间内在二维Yee网格上移动,分为三种涉及不同元胞数目的情形.本文列出并分析了这三类情形所对应的线性代数方程组,同时研究了每个方程组所对应的三个特解:V方法、E方法和U方法所给的电流密度公式.一个带有一阶形状函数的宏粒子单位时间内在三维Yee网格上移动,分为八种涉及不同元胞数目的情形.针对其中最常见同时也最简单的一类情形,本文列出并分析了其所对应的线性代数方程组,同时研究了该方程组所对应的两个特解:V方法、E方法所给出的电流密度公式.值得一提的是U方法给出的三维公式,不满足电荷守恒.
从本文的分析可知,我们获得了一定条件下的通解,即:所有电荷守恒的电流分配方案.从这些通用公式的推导可以看出,公式对宏粒子形状函数的阶数没有限制并且可以推广到其它网格上去.同时从通解出发,我们可以想办法得到一个“最优解”,只要“最优”标准被确定.
A 附录
A1 相关形因子
表 1 涉及四个元胞时相关形因子(二维)
| Form-factor | |
表 2 涉及六个元胞时相关形因子(二维)
| Form-factor | ||
表 3 涉及七个元胞时相关形因子(二维)
| Form-factor | ||||
表 4 涉及八个元胞时相关形因子(三维,最常见情形)
| Form-factor(1st order) | |
A2 三维最常见情形下U方法给出的公式
在如图 4所示的、涉及八个元胞的最常见且最简单的三维情形下,根据U方法,有
对于图 4所示的某一元胞,如元胞
即,不满足离散的电荷连续性方程.
参考文献
The virtual particle electromagnetic particle-mesh method
Three-dimensional simple conformal symplectic particle-in-cell methods for simulations of high power microwave devices
User-configurable MAGIC for electromagnetic PIC calculations
UNIPIC code for simulations of high power microwave devices
Exact charge-conserving scatter-gather algorithm for particle-in-cell simulations on unstructured grids:A geometric perspective
An object-oriented electromagnetic PIC code
Axisymmetric charge-conservative electromagnetic particle simulation algorithm on unstructured grids:Application to microwave vacuum electronic devices
DOI:10.1016/j.jcp.2017.06.016 [本文引用: 1]
Experimental study on a high-power subterahertz source generated by an overmoded surface wave oscillator with fast startup
Experimental study on a high-power subterahertz source generated by an overmoded surface wave oscillator with fast startup
Analysis of multipactor effects by a particle-in-cell algorithm integrated with secondary electron Emission model on irregular grids
Numerical simulations of high power microwave dielectric interface breakdown involving outgassing
DOI:10.1063/1.3432715 [本文引用: 1]
Charge-conserving grid based methods for the Vlasov-Maxwell equations
Rigorous charge conservation for local electromagnetic field solvers
Exact charge conservation scheme for particle-in-cell simulation with an arbitrary form-factor
A new charge conservation method in electromagnetic particle-in-cell simulations
Numerical charge conservation in particle-in-cell codes