1 引言
1973年Black和Scholes推导出著名的Black-Scholes期权定价公式[1],是金融数学领域的一个里程碑.然而, Black-Scholes模型的一系列假设(如波动率为常数,价格过程服从对数正态分布、市场是完备的)使得期权价格与市场观察价格存在较大差异.尤其1987年金融危机的爆发, Black-Scholes模型中期权价格与市场报价的偏差更加显著.从那时起,人们不断的探寻能够精确复制股票价格动态的定价模型.指数Lévy模型通常被当作Black-Scholes模型的替代模型,因为Lévy过程允许股票价格跳跃,能够有效的描述股票价格具有"尖峰厚尾"及对数收益非对称等特点.
跳-扩散模型[2]是指数Lévy模型中一类非常重要的模型,该模型最早由Merton提出.跳-扩散模型在Black-Scholes模型基础上增加非连续的跳跃,连续部分表示的是每天价格过程的演变,跳跃代表稀少事件.与Black-Scholes模型相比,跳-扩散模型更具有灵活性[3],从而能更好的模拟金融市场数据.然而,跳-扩散模型下市场是不完备的,此时存在许多等价鞅测度,从而对应着有许多无套利价格.为了得到一致的无套利价格,需要在所有等价鞅测度中选择一个最优(相对于某些标准)的鞅测度[4],均值修正法是获取等价鞅测度的一种常用的方法[5].另外,指数Lévy模型下封闭形式的概率密度函数往往是未知的,但其特征函数通常是可以得到的,因此利用特征函数对期权进行定价是非常必要的. Carr和Madan提出基于特征函数计算期权价格的快速傅里叶变换算法(FFT)[6],在此基础上, Fang和Oosterlee提出了利用傅里叶余弦级数计算欧式期权价格的COS方法[7],该方法利用了特征函数与密度函数傅里叶余弦展开系数之间的特殊关系,其收敛速度和计算难度都优于FFT方法.
本文对跳-扩散模型下期权定价及参数校准问题进行研究,推导出了均值修正等价鞅测度下跳-扩散模型的风险中性特征函数,利用COS方法对跳-扩散模型进行定价,并证明了算法的收敛性.然后,利用相对熵正则化方法对跳-扩散模型参数进行校准,数值实验表明该方法是准确、可靠的.最后利用S&P500期权市场数据对Merton跳-扩散模型进行参数校准,得到了较好的校准结果,利用校准参数重构的波动率曲面与市场实际波动率曲面相吻合.
2 预备知识
2.1 指数Lévy模型
假设市场上有两种资产,一种为无风险资产(如债券),其价格过程为
其中
其中
如果关于
由Lévy-Itô分解公式,
其中
Black-Scholes模型的驱动过程可由
基于Lévy过程的跳-扩散模型是同时包含布朗运动和复合泊松过程的随机过程,可由如下方程给出
其中
2.2 跳-扩散模型的均值修正等价鞅测度
对于指数Lévy模型,均值修正法是获取等价鞅测度的常用方法,其基本思想是通过修正Lévy过程的均值,获取某个与市场概率测度
定理2.1 假设
证 由于这种变换只改变了
有唯一解
引理2.1[12] 均值修正鞅测度
定理2.2 设均值修正鞅测度
如果
证 在均值修正鞅测度
由
由引理2.1和定理2.2可知均值修正鞅测度
命题2.1 Black-Scholes模型中,
Merton跳-扩散模型中,
3 跳-扩散模型下期权定价方法
如果密度函数
引理3.1[1] 在Black-Scholes模型下,欧式看涨期权在
其中
引理3.2[2] 在Merton跳-扩散模型下,欧式看涨期权在
其中
3.1 欧式期权的COS定价方法
在等价鞅测度
其中
首先,把(3.3)式的积分区间截断为某个满足精度要求的有限区间
对于给定的误差限TOL, (3.3)式可近似表示为
第二步,对密度函数
其中
把(3.6)式代入到(3.5)式,并交换求和与积分运算次序,得
其中
由于当
第三步,定义条件特征函数
那么,系数
其中
因此,
由
在指数Lévy模型下,条件特征函数
COS方法积分截断范围
其中
命题3.1 Merton跳-扩散模型中,
其中
3.2 COS定价方法误差分析
记
由
(1)由
由于期权价格
(2)由
对于给定
其中
其中
(3)由
其中
由三部分误差限及三角不等式,可得
其中
下面通过数值实验将COS方法的数值解与Merton模型下欧式看涨期权的精确解进行比较,参数选取如下:
由表 1可以看出,随着截取数列项数
表 1 COS方法的误差收敛速度及运行时间
| N | 32 | 64 | 128 | 256 | 512 | |
| 运行时间(s) | 0.018 | 0.019 | 0.020 | 0.022 | 0.024 | |
| 绝对误差 | 13.486 | 1.007 | 2.378e-06 | 3.561e-9 | 3.561e-9 | |
| 运行时间(s) | 0.016 | 0.019 | 0.019 | 0.021 | 0.024 | |
| 绝对误差 | 13.758 | 1.009 | 2.400e-06 | 3.535e-9 | 3.535e-9 | |
| 运行时间(s) | 0.018 | 0.019 | 0.021 | 0.022 | 0.025 | |
| 绝对误差 | 13.770 | 1.013 | 2.380e-06 | 3.549e-9 | 3.549e-9 |
4 参数校准
参数校准问题与给定模型参数进行期权定价过程是两个互逆的问题,参数校准是通过观测到的期权市场价格求解模型中的未知参数,即寻找合适的参数
问题1 对于给定的一组到期日为
其中
由于市场价格存在一定的噪声,市场观测价格与模型价格不可能精确匹配,因此校准问题转化为两种价格的最佳近似问题,通常可采用非线性最小二乘方法求解.
4.1 非线性最小二乘方法
利用非线性最小二乘(NLS)方法求解问题1,即对下列函数最小化
其中
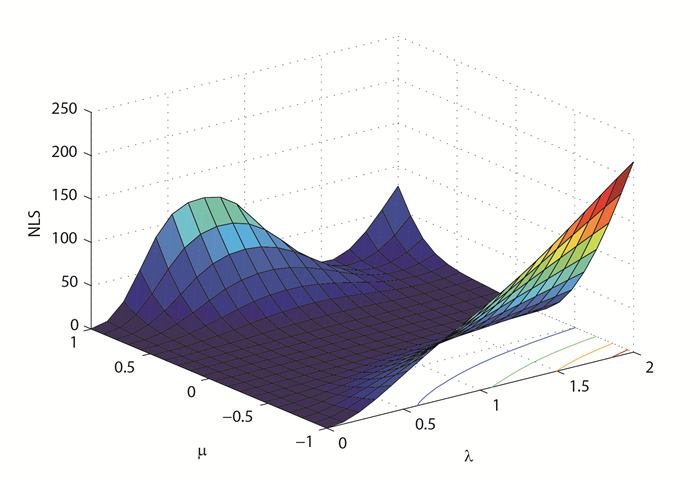
图 1给出了当固定参数
图 1
4.2 相对熵正则化方法
本文选择相对熵(Kullback-Leibler距离)
(1)相对熵函数是凸函数;
(2)相对熵函数保证了校准测度
(3)如果先验测度是风险中性测度,相对熵函数保证了校准测度
(4)相对熵函数易于计算.
定义4.1[10] 令
令
由
引理4.1[10] 假设
定理4.1 假设
那么, Merton跳-扩散模型的相对熵函数为
证 由引理4.1可知
而
把(4.8)和(4.9)式代入到(4.7)式可知定理4.1成立.
增加相对熵作为惩罚函数,问题1可转化对如下函数进行最小化
其中
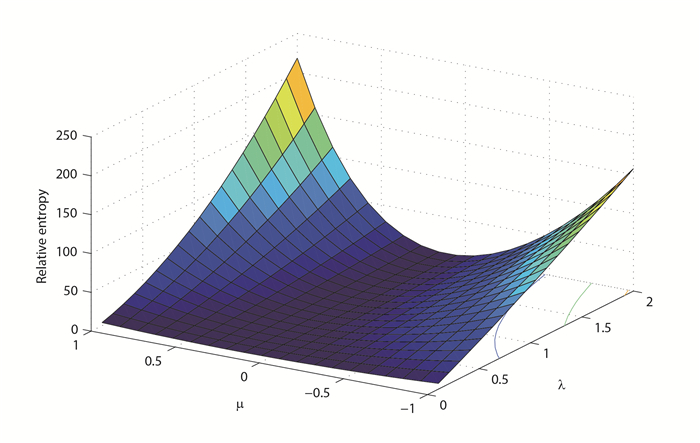
图 2
首先,计算非线性方差问题(4.1)式得到扩散估计
然后,固定
接下来,
5 数值实验与实证分析
5.1 数值实验
本节对前面给出的校准方法进行数值实验.首先,在给定参数条件下,利用COS方法生成Merton模型下期权价格的模拟数据.然后,利用Matlab R2012b,调用fmincon函数对目标函数进行优化求解.
假设市场服从Merton模型,特征三元组为
其中
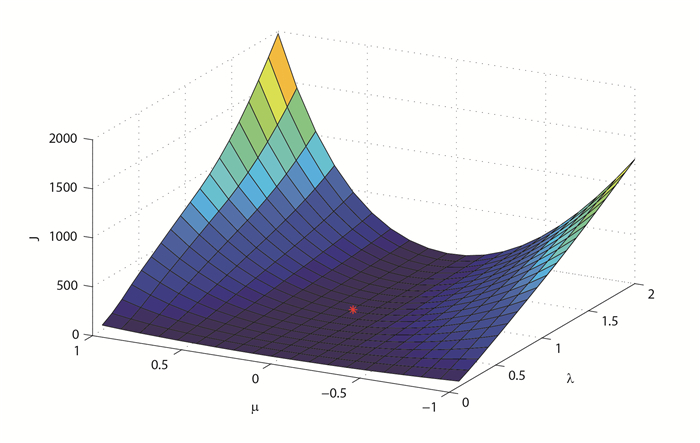
图 3
为了计算简单,固定参数
首先,利用NLS方法求解(4.1).运算结果表明:当初值取
接下来,利用相对熵方法进行正则化校准.数值计算主要包括以下四步:
(1)选择权重:
(2)先验参数选取:
(3)选择正则化参数:
(4)在给定的
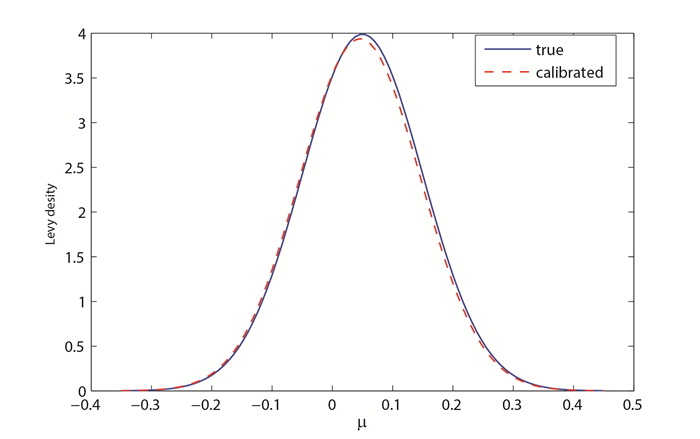
图 4给出了真实Lévy测度与校准测度,通过比较可以发现校准所得Lévy测度与真实的Lévy测度曲线是非常接近的,校准结果具有较高的精度.因此相对熵正则化方法是一种可行、有效的方法.
图 4
5.2 实证分析
本节利用相对熵正则化方法对市场数据进行实证分析.数据选自2015年4月3日S&P500股指期权,当日指数收盘价格
含有未知参数的Merton模型的期权价格
(1)选择权重:选用市场买卖差价利用(4.2)计算;
(2)先验参数选取:利用非正则化的NLS方法对(4.1)最小化的解作为先验参数;
(3)选择正则化参数
(4)在给定的
我们通过下列根均值误差(RMSE)来检验校准的质量
表 2给出了利用不同到期日的S&P500欧式看涨期权市场数据分别对Black-Scholes模型和Merton模型的参数校准结果.可以看出Merton跳-扩散模型的RMSE值小于Black-Scholes模型的RMSE的值,这意味着Merton模型比Black-Scholes模型能更好的拟合市场数据.这主要反映在自由度上,具有更多自由度的模型比具有较小自由度的模型能更好的模拟市场数据.另一方面,可以看出对于Merton模型,参数值在不同的到期日得到的结果是不同的,并且较长的期限,平均跳跃幅度及跳跃强度都随持有期间长度而减少.
表 2 S&P500期权参数校准结果
| 到期日 | 模型 | RMSE | ||||
| Merton模型 | 0.0656 | 8.2454 | -0.0341 | 0.0440 | 0.8416 | |
| Black-Scholes模型 | 0.1247 | 2.8718 | ||||
| Merton模型 | 0.0520 | 5.9989 | -0.0388 | 0.0396 | 0.3094 | |
| Black-Scholes模型 | 0.1136 | 4.9638 | ||||
| Merton模型 | 0.0648 | 1.6550 | -0.0998 | 0.0176 | 0.2825 | |
| Black-Scholes模型 | 0.1164 | 6.2999 | ||||
| Merton模型 | 0.0662 | 0.8905 | -0.1412 | 0.0467 | 0.5395 | |
| Black-Scholes模型 | 0.1252 | 11.9545 |
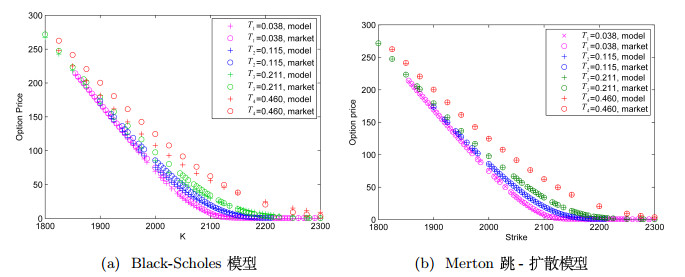
图 5给出了利用校准参数所得欧式期权价格与市场期权价格的比较,可以看出Merton跳-扩散模型下期权的价格与S&P500股指期权的市场数据是非常接近的,而由Black-Scholes模型计算的期权的价格与S&P500市场数据有较大的差异,这进一步说明了Merton跳-扩散模型比Black-Scholes模型能更好的模拟S&P500市场.
图 5
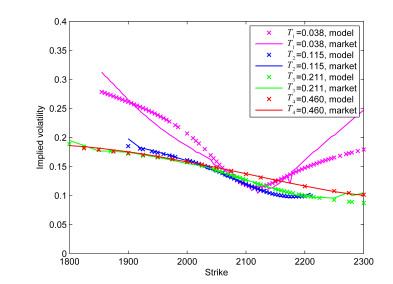
图 6给出了四个不同到期日的校准的隐含波动率与市场真实波动率的比较.由图可以看出Merton跳-扩散模型有效地捕捉了S&P500指数期权的隐含波动率曲线特征,校准结果是比较满意的.但当距离到期日时间较短时,校准结果相对较差,主要是因为临近到期日期权交易频繁,波动率变化较大,特征很难被有效的捕捉.而距到期日在一个月以上的,波动率变化较小,校准结果比较理想.
图 6
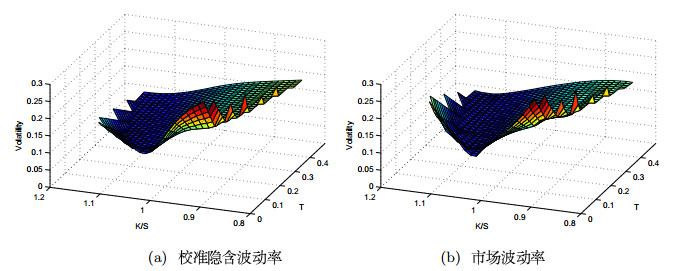
图 7给出了Merton跳-扩散模型下重构的隐含波动率曲面以及市场真实波动率曲面,可以看出Merton跳-扩散模型重现了隐含波动率的"微笑"和"偏斜"的特征,并且与市场真实波动率曲面拟合效果较好.
图 7
6 结论
本文主要研究了跳-扩散模型下的期权定价问题及参数校准问题.首先,给出了Merton跳-扩散模型下期权定价的COS方法,分析了COS方法的定价误差,并通过数值实验验证了COS方法的有效性.其次,对Merton跳-扩散模型参数进行校准,结果表明非线性最小二乘方法得到的校准结果是不稳定的.采用相对熵方法进行正则化可以增加目标函数的凸性,从而可以得到校准问题的唯一性.然后,通过数值模拟实验验证了相对熵正则化方法的准确性和有效性.最后,利用相对熵正则化方法对S&P500股指期权数据进行参数校准,并利用校准参数重构了Merton跳-扩散模型下隐含波动率的曲面,得到了比较满意的校准结果.
参考文献
The pricing of option and corporate liabilities
Option pricing when underlying stock returns are discontinuous
DOI:10.1016/0304-405X(76)90022-2 [本文引用: 2]
Option pricing models with jumps:integro-differential equations and inverse problems
The fundamental theorem of asset pricing for unbounded stochastic processes
A note on the mean correcting martingale measure for geometric Lévy processes
DOI:10.1016/j.aml.2010.11.011 [本文引用: 2]
Option valution using the fast Fourier transform
A novel option pricing method based on Fourier-cosine series expansions
Calibration of jump-diffusion option pricing models:A robust non-parametric approach
DOI:10.2139/ssrn.332400 [本文引用: 1]
Non-parametric calibration of jump-diffusion option pricing models