跳-扩散模型下期权定价方法及参数校准

数学物理学报 ›› 2019, Vol. 39 ›› Issue (3): 649-663.

跳-扩散模型下期权定价方法及参数校准

许聪聪^1,²,许作良^1,*()

¹ 中国人民大学数学学院北京 100872
² 石家庄铁路职业技术学院石家庄 050041

收稿日期:2017-12-28 出版日期:2019-06-26 发布日期:2019-06-27
通讯作者: 许作良 E-mail:xuzl@ruc.edu.cn
基金资助:
国家自然科学基金(11571365);国家自然科学基金(11401162);河北省高等学校科学技术研究重点项目(ZD2019080)

Option Pricing Method and Parameter Calibration for Jump-Diffusion Model

Congcong Xu^1,²,Zuoliang Xu^1,*()

¹ School of Mathematics, Renmin University of China, Beijing 100872
² Shijiazhuang Institute of Railway Technology, Shijiazhuang 050041

Received:2017-12-28 Online:2019-06-26 Published:2019-06-27
Contact: Zuoliang Xu E-mail:xuzl@ruc.edu.cn
Supported by:
the NSFC(11571365);the NSFC(11401162);the Key Projects of Science and Technology Research in Colleges and Universities in Hebei Province(ZD2019080)

摘要/Abstract

摘要：

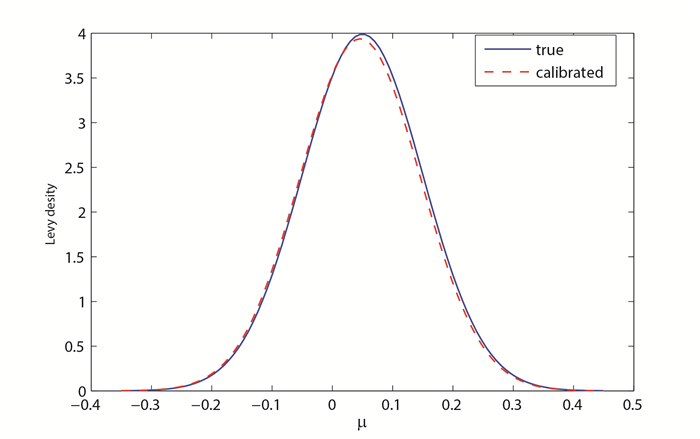
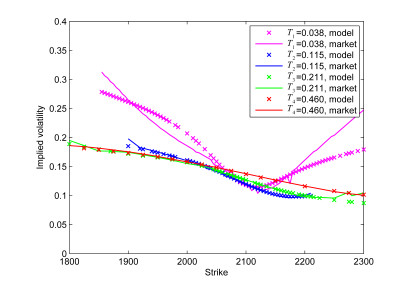
该文对跳-扩散模型下期权定价方法及参数校准问题进行研究.首先，推导出了跳-扩散模型在均值修正等价鞅测度下的风险中性特征函数，利用COS方法对跳-扩散模型进行期权定价，分析了COS方法的定价误差，并通过数值实验验证了COS定价方法的有效性；然后，采用相对熵正则化方法对跳-扩散模型进行参数校准，通过数值模拟实验验证了校准方法的准确性和可靠性；最后，利用S&P500市场数据对模型参数进行校准.结果表明：不同到期日期权数据校准结果有很大不同，Merton跳-扩散模型比Black-Scholes模型能更好的模拟市场数据.

关键词: 跳-扩散模型, 期权定价, 参数校准, COS方法, 正则化

Abstract:

In this paper, the pricing method and parameter calibration of jump-diffusion model are investigated. First, the risk-neutral characteristic function of jump-diffusion model is derived under the mean correctiong equivalent martingale measure. The option under jump-diffusion model is priced by using the COS pricing method. Then, the pricing error of the COS algorithm is analyzed and the effectiveness of the COS pricing method is verified through numerical experiment. Subsequently, the parameters of the jump-diffusion model are calibrated by the relative entropy regularization method. Numerical experiments demonstrate the accuracy and reliability of the proposed method. Finally, the calibration method is tested by analyzing the S&P500 market data. The results show that the values of calibrated parameter are qualitatively for each maturity. Moreover, the results indicate a better fitting to the market data for the Merton jump-diffusion model in comparison to the Black-Scholes model.

Key words: Jump-diffusion models, Option pricing, Parameter calibration, COS method, Regularization

中图分类号:

O211.6

许聪聪,许作良. 跳-扩散模型下期权定价方法及参数校准[J]. 数学物理学报, 2019, 39(3): 649-663.

Congcong Xu,Zuoliang Xu. Option Pricing Method and Parameter Calibration for Jump-Diffusion Model[J]. Acta mathematica scientia,Series A, 2019, 39(3): 649-663.

图/表 9

表 1

图 1

图 2

图 3

图 4

表 2

图 5

图 6

图 7

参考文献 12

1	Black F , Scholes M . The pricing of option and corporate liabilities. J Political Econom, 1973, 81: 637- 659 doi: 10.1086/260062
2	Merton R . Option pricing when underlying stock returns are discontinuous. J Finan Econom, 1976, 3: 125- 144 doi: 10.1016/0304-405X(76)90022-2
3	Cont R , Tankov P , Voltchkova E . Option pricing models with jumps:integro-differential equations and inverse problems. European Congress on Computational Methods in Applied Sciences and Engineering, 2004, 1- 20
4	Delbaen F , Schachermayer W . The fundamental theorem of asset pricing for unbounded stochastic processes. Math Anna, 1996, 312: 215- 250
5	Yao L G , Yang G , Yang X Q . A note on the mean correcting martingale measure for geometric Lévy processes. Appl Math Lett, 2011, 24: 593- 597 doi: 10.1016/j.aml.2010.11.011
6	Carr P , Madan D . Option valution using the fast Fourier transform. J Comput Finance, 1999, 3: 463- 520
7	Fang F , Oosterlee C W . A novel option pricing method based on Fourier-cosine series expansions. SIAM J Sci Comput, 2008, 31: 826- 848
8	Cont R , Tankov P . Financial Modelling with Jump Processes. New York: Chapman & Hall/CRC Press, 2004
9	Cont R , Tankov P . Calibration of jump-diffusion option pricing models:A robust non-parametric approach. SSRN Electronic J, 2002 doi: 10.2139/ssrn.332400
10	Cont R , Tankov P . Non-parametric calibration of jump-diffusion option pricing models. J Comput Finance, 2004, 7: 1- 49
11	Schoutens W . Lévy Process in Finance:Pricing Financial Derivatives. New York: Wiley, 2003
12	Miyahara Y. Martingale measures for the geometric lévy process models. Discussion Papers in Economics, Nagoya City University, 2005, 431:1-14

	N	32	64	128	256	512
$K=90$	运行时间(s)	0.018	0.019	0.020	0.022	0.024
	绝对误差	13.486	1.007	2.378e-06	3.561e-9	3.561e-9
$K=100$	运行时间(s)	0.016	0.019	0.019	0.021	0.024
	绝对误差	13.758	1.009	2.400e-06	3.535e-9	3.535e-9
$K=110$	运行时间(s)	0.018	0.019	0.021	0.022	0.025
	绝对误差	13.770	1.013	2.380e-06	3.549e-9	3.549e-9

到期日	模型	$\sigma^Q$	$\lambda^Q$	$\mu^Q$	$\delta^Q$	RMSE
$T_1=0.038$	Merton模型	0.0656	8.2454	-0.0341	0.0440	0.8416
	Black-Scholes模型	0.1247				2.8718
$T_2=0.115$	Merton模型	0.0520	5.9989	-0.0388	0.0396	0.3094
	Black-Scholes模型	0.1136				4.9638
$T_3=0.211$	Merton模型	0.0648	1.6550	-0.0998	0.0176	0.2825
	Black-Scholes模型	0.1164				6.2999
$T_4=0.460$	Merton模型	0.0662	0.8905	-0.1412	0.0467	0.5395
	Black-Scholes模型	0.1252				11.9545

[1]	肖爽, 蹇明, 陈爱香, 蹇贝. 模糊环境中跳扩散模型下带交易费用的期权定价方法[J]. 数学物理学报, 2015, 35(1): 118-130.
[2]	杨帆, 傅初黎, 李晓晓. 修正的Helmholtz方程未知源识别的Fourier截断正则化方法[J]. 数学物理学报, 2014, 34(4): 1040-1047.
[3]	赵振宇, 由雷. 求解热源识别问题的修正吉洪诺夫正则化方法[J]. 数学物理学报, 2014, 34(1): 186-192.
[4]	孙玉东, 师义民, 吴敏. 参数依赖股票价格情形下的障碍期权定价[J]. 数学物理学报, 2013, 33(5): 912-925.
[5]	冯立新, 李媛. 确定热流的非标准逆热传导问题的小波正则化方法[J]. 数学物理学报, 2012, 32(4): 709-719.
[6]	杨帆, 傅初黎, 李晓晓. 修正的Helmholtz方程未知源识别反问题[J]. 数学物理学报, 2012, 32(3): 557-565.
[7]	韩传峰, 张超 . 用复参数迭代法解不适定自共轭紧算子方程[J]. 数学物理学报, 2011, 31(4): 887-891.
[8]	陈平炎, 李远梅. 鞅差序列滑动和过程的极限结果[J]. 数学物理学报, 2011, 31(1): 179-187.
[9]	杨帆, 傅初黎. Poisson 方程热源识别反问题[J]. 数学物理学报, 2010, 30(4): 1080-1087.
[10]	安荣, 李开泰. Plate Contact问题的混合有限元逼近[J]. 数学物理学报, 2010, 30(3): 666-676.
[11]	孔令海, 郇中丹. 灰度图像复原的一种空间适应性向前向后扩散模型[J]. 数学物理学报, 2009, 29(6): 1771-1784.
[12]	黄惠;费浦生;袁媛. 关于单电子电脑断层摄影图像重建的反问题[J]. 数学物理学报, 2008, 28(1): 46-058.
[13]	坚雄飞;易法槐. 分期付款购房模型及其抛物障碍问题[J]. 数学物理学报, 2007, 27(6): 987-995.
[14]	傅初黎, 邱春雨, 赵华. 求解一般抛物方程侧边值问题的Fourier正则化方法[J]. 数学物理学报, 2005, 25(6): 806-810.
[15]	黄小为, 吴传生, 朱华平. 基于奇异值分解建立的一种新的正则化方法[J]. 数学物理学报, 2005, 25(3): 331-336.