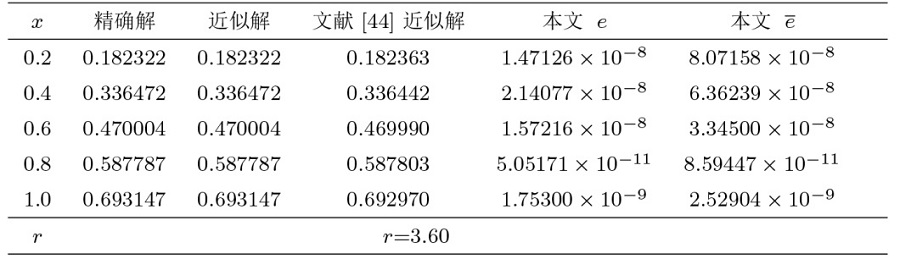
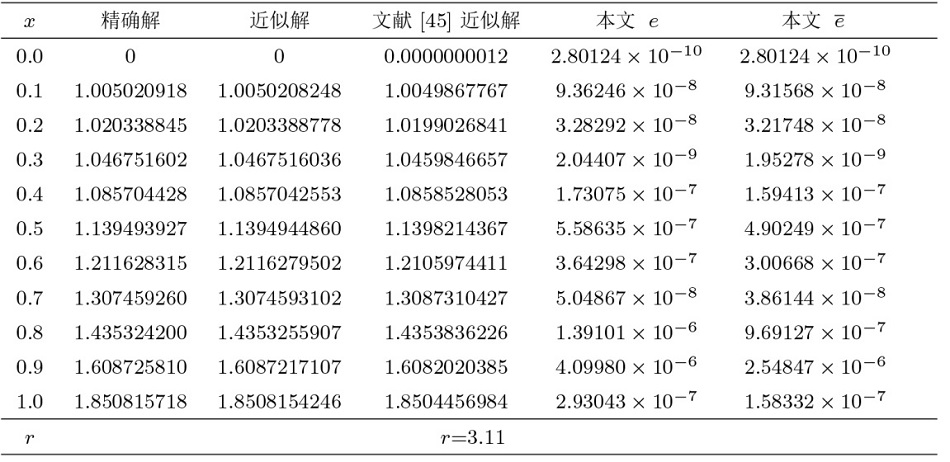
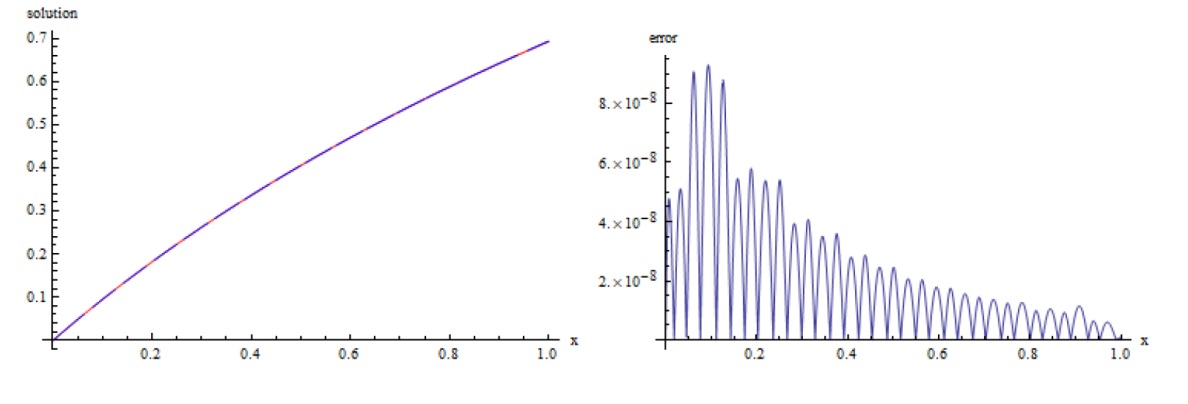
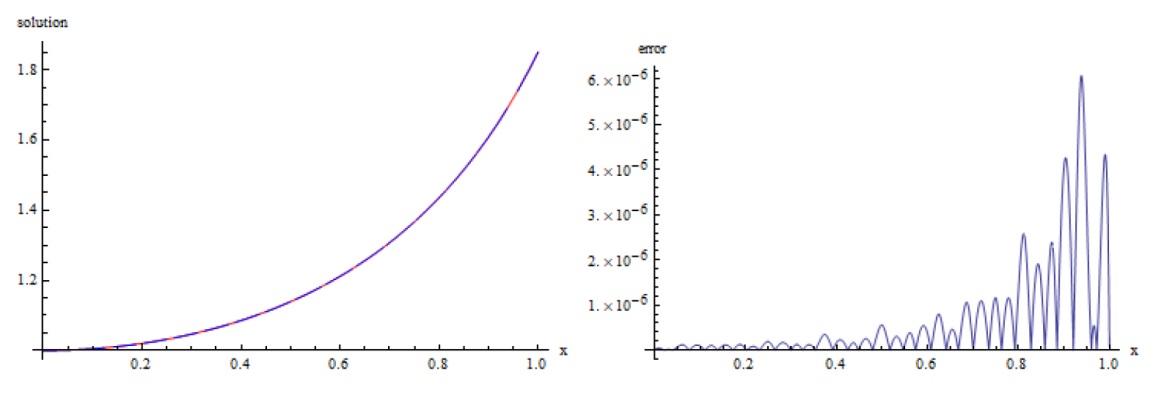
数学物理学报 ›› 2024, Vol. 44 ›› Issue (5): 1283-1301.
第二类 Volterra 型积分方程的数值算法研究
- 哈尔滨师范大学数学科学学院 哈尔滨 150025
-
收稿日期:2023-08-07修回日期:2024-04-16出版日期:2024-10-26发布日期:2024-10-16 -
通讯作者:*牛晶, E-mail:njirwin@163.com -
基金资助:国家青年自然科学基金项目(12101164);哈尔滨师范大学硕士研究生创新科研项目(HSDSSCX2023-12)
Numerical Algorithm for Volterra Type Integral Equation of the Second Kind
Dai Xuefei,Yu Yikang,Niu Jing*( )
)
- School of Mathematical and Sciences, Harbin Normal University, Harbin 150025
-
Received:2023-08-07Revised:2024-04-16Online:2024-10-26Published:2024-10-16 -
Supported by:Youth Fund of NSFC(12101164);Postgraduate Innovative Scientific Research Project of Harbin Normal University(HSDSSCX2023-12)
摘要:
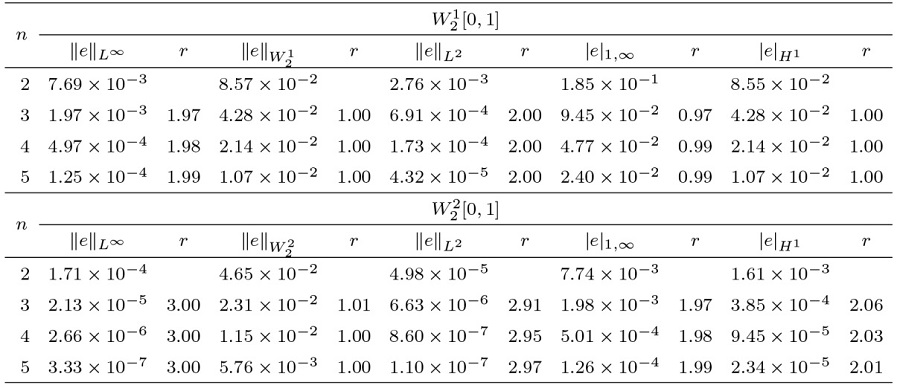
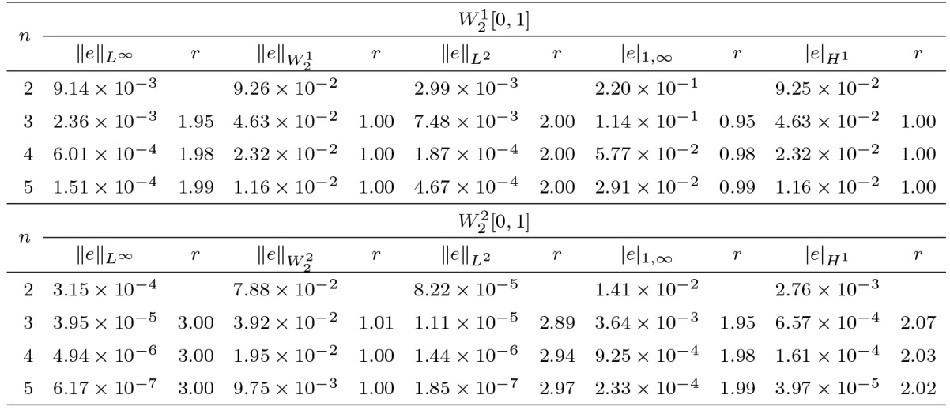
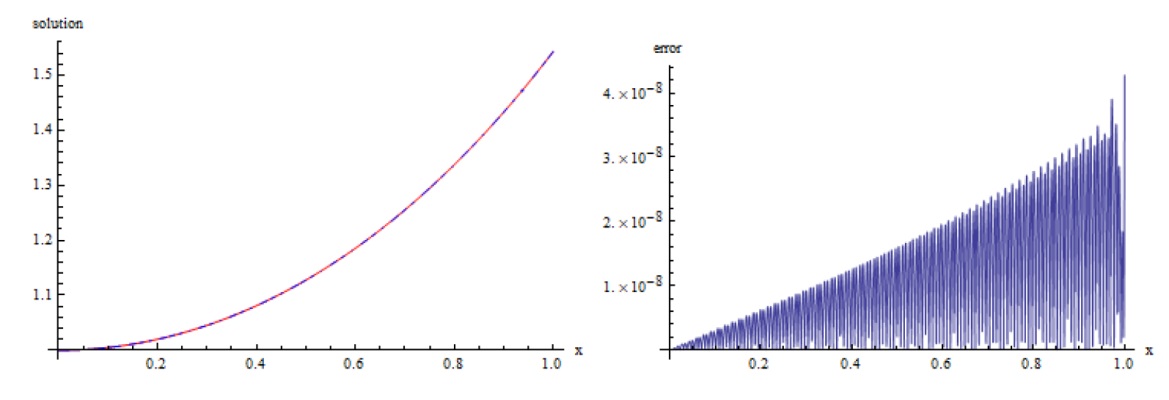
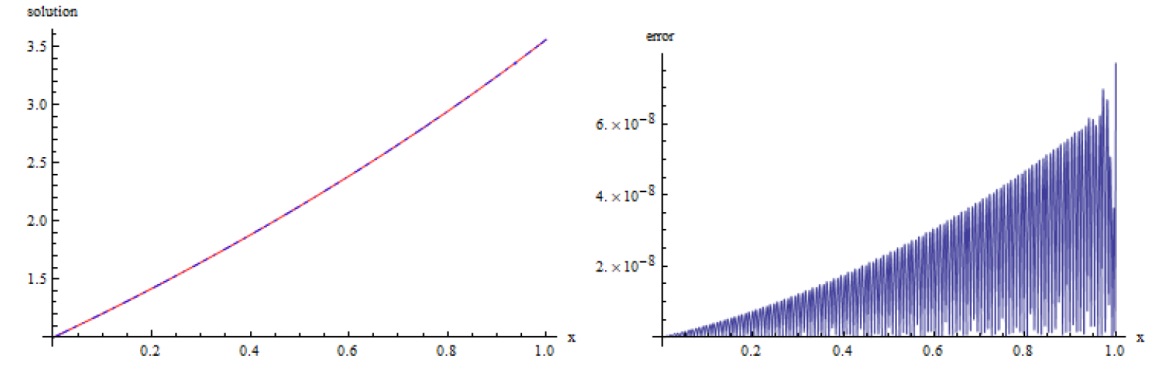
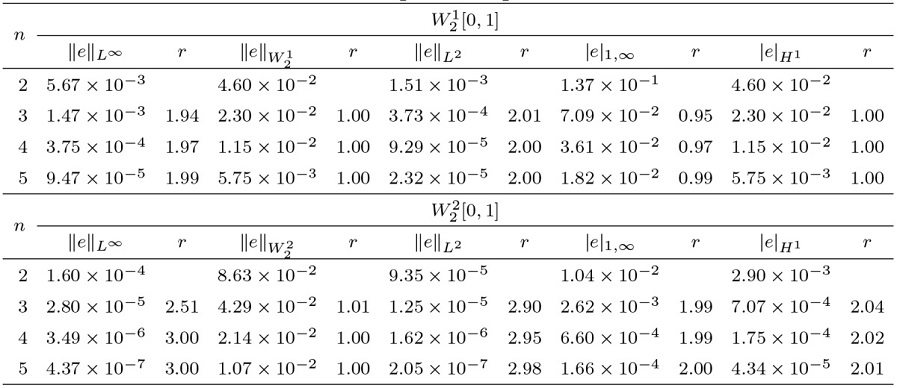
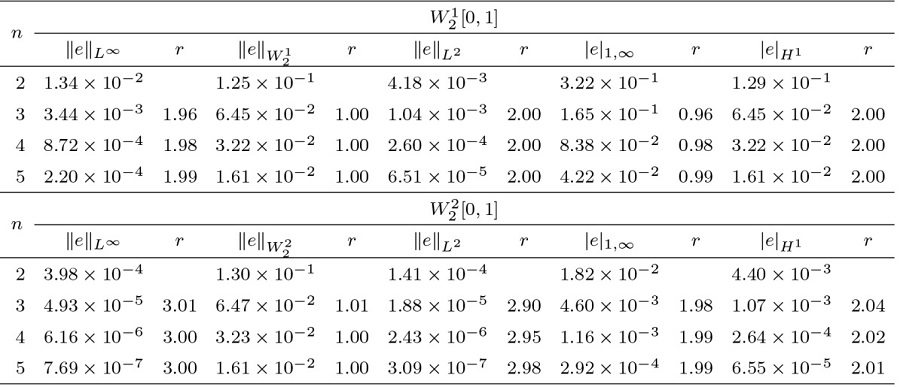
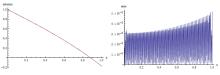
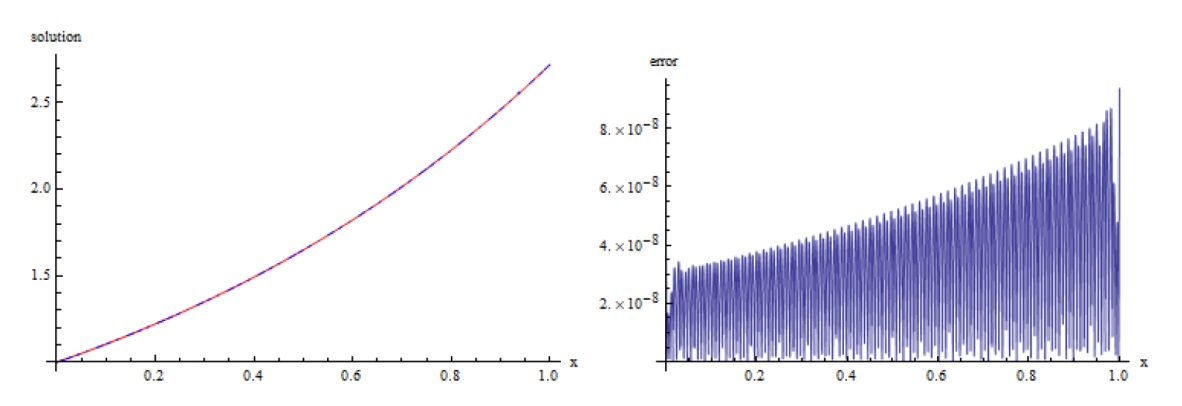
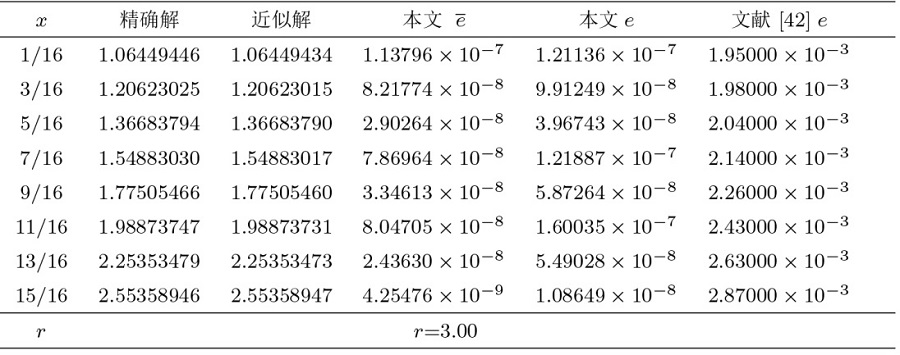
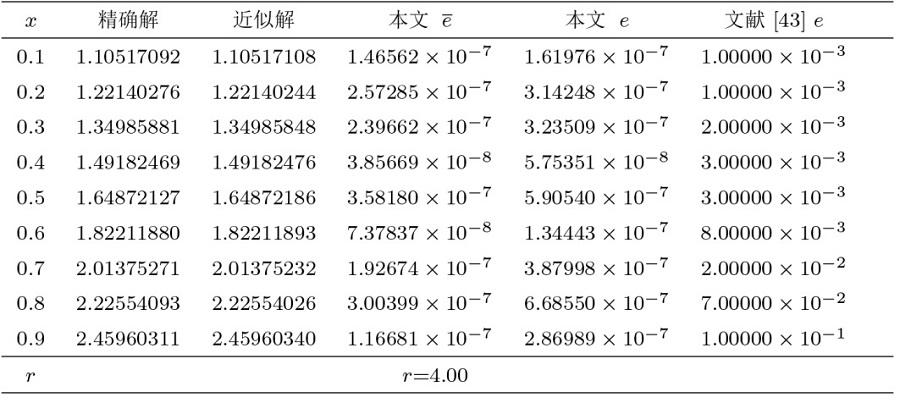
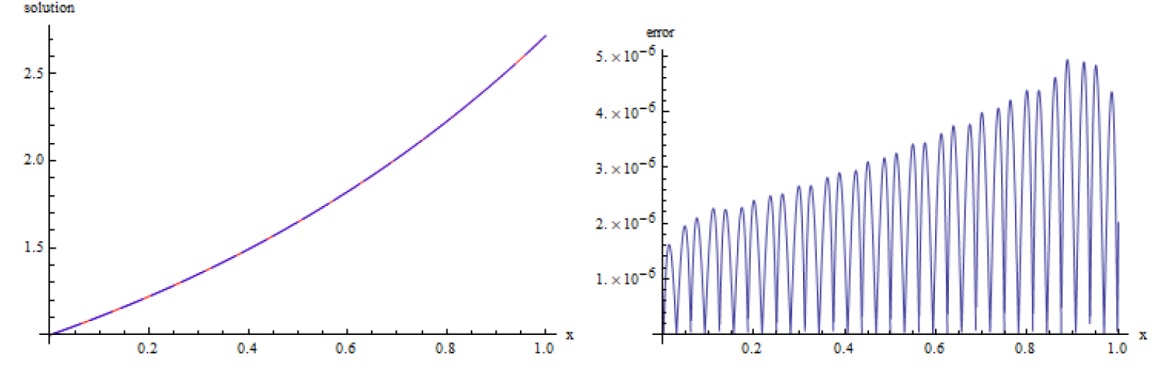
该文将最小二乘法与再生核法相结合, 提出了求解第二类 Volterra 型积分方程的新算法. 通过构造再生核空间的多尺度正交基, 得到了模型的解的表达式. 为了减少计算量, 简化计算过程, 文章利用最小二乘法将模型转化为线性代数方程进而得到
中图分类号:
- O241.8
引用本文
代雪飞, 于一康, 牛晶. 第二类 Volterra 型积分方程的数值算法研究[J]. 数学物理学报, 2024, 44(5): 1283-1301.
Dai Xuefei, Yu Yikang, Niu Jing. Numerical Algorithm for Volterra Type Integral Equation of the Second Kind[J]. Acta mathematica scientia,Series A, 2024, 44(5): 1283-1301.
使用本文
| [1] | Salon S, Chari M. Numerical Methods in Electromagnetism. Beijing: Academic Press, 1999 |
| [2] |
Cheng Z. Quantum effects of thermal radiation in a Kerr nonlinear blackbody. J Opt Soc Amer B Opt Phys, 2002, 19(7): 1692-1705
doi: 10.1364/JOSAB.19.001692 |
| [3] | Chew W C, Tong M S, Hu B. Integral Equation Methods for Electromagnetic and Elastic Waves. Berlin: Springer Nature, 2022 |
| [4] | Bloom F. Asymptotic bounds for solutions to a system of damped integro-differential equations of electromagnetic theory. J Math Anal Appl, 1980, 73(2): 524-542 |
| [5] | Wazwaz A M. Linear and Nonlinear Integral Equations. Berlin: Springer, 2011 |
| [6] | Tang Q, Waxman D. An integral equation describing an asexual population in a changing environment. Nonlinear Anal, 2003, 53(5): 683-699 |
| [7] | Corduneanu C. Integral Equations and Applications. Cambridge: Cambridge University, Press, 1991 |
| [8] | Schiavone P, Constanda C, Mioduchowski A. Integral Methods in Science and Engineering. Boston: Birkhäuser, 2012 |
| [9] | Abaoub A E, Shkheam A S, Zali S M. The Adomian decomposition method of Volterra integral equation of second kind. Am J Appl Math, 2018, 6(4): 142-148 |
| [10] | 曾志刚. Volterra 积分微分方程的稳定性. 数学物理学报, 2001, 21A(1): 48-54 |
| Zeng Z G. Stability of Volterra integro differential equations. Acta Math Sci, 2001, 21A(1): 48-54 | |
| [11] | 袁海龙, 李艳玲. 一类具有 Lotka-Volterra 竞争模型共存解的存在性与稳定性. 数学物理学报, 2017, 37A(1): 173-184 |
| Yuan H L, Li Y L. The existence and stability of coexistence solutions of a kind of Lotka-Volterra competition model. Acta Math Sci, 2017, 37A(1): 173-184 | |
| [12] | Chu Y M, Ullah S, Ali M, et al. Numerical investigation of Volterra integral equations of second kind using optimal homotopy asymptotic method. Appl Math Comput, 2022, 430: 127304 |
| [13] | Khidir A A. A new numerical technique for solving Volterra integral equations using Chebyshev spectral method. Math Probl Eng, 2021, 2021: 1-11 |
| [14] | Bulai I M, De Bonis M C, Laurita C, et al. MatLab Toolbox for the numerical solution of linear Volterra integral equations arising in metastatic tumor growth models. Dolomites Research Notes on Approximation, 2022, 15(2): 13-24 |
| [15] | 冯立新, 杨晓旭. 解带有扰动数据的第一类 Volterra 积分方程的谱正则化方法. 数学物理学报, 2020, 40A(3): 650-661 |
| Feng L X, Yang X X. Spectral regularization method for solving Volterra integral equation of the first kind with perturbed data. Acta Math Sci, 2020, 40A(3): 650-661 | |
| [16] | Hesameddini E, Shahbazi M. A reliable algorithm based on the shifted orthonormal Bernstein polynomials for solving Volterra-Fredholm integral equations. Journal of Taibah University for Science, 2018, 12(4): 427-438 |
| [17] | Varah J M. A spline least squares method for numerical parameter estimation in differential equations. SIAM J Sci Comput, 1982, 3(1): 28-46 |
| [18] | Wang W X, Xu Y, Han X L, Gao M L, et al. A study of function-based wind profiles based on least squares method: A case in the suburbs of Hohho. Energy Reports, 2022, 8: 4303-4318 |
| [19] | Rahman M H, Habib A. Impact of economic and noneconomic factors on inflow of remittances into bangladesh: Application of robust least squares method. Finance and Economics Review, 2021, 3(1): 51-62 |
| [20] | 张晶, 余旌胡. 线性回归模型参数估计方法的分辨率. 数学物理学报, 2020, 40A(5): 1381-1392 |
| Zhang J, Yu J H. Parameter resolution of estimation methods for linear regression models. Acta Math Sci, 2020, 40A(5): 1381-1392 | |
| [21] | 马奕佳, 薛留根, 芦飞. 缺失数据下部分非线性变系数 EV 模型的统计推断. 数学物理学报, 2020, 40A(2): 460-474 |
| Ma Y J, Xue L g, Lu F. Statistical inference in partially nonlinear varying-coefficient Errors-Variables models with missing responses. Acta Math Sci, 2020, 40A(2): 460-474 | |
| [22] | 冯三营, 薛留根, 范承华. 非线性半参数回归模型中参数的经验似然置信域. 数学物理学报, 2009, 29A(5): 1338-1349 |
| Feng S Y, Xue L G, Fan C H. Empirical likelihood confidence regions of the parameters in nonlinear semiparametric regression models. Acta math sci, 2009, 29A(5): 1338-1349 | |
| [23] | Salehi R, Dehghan M. A generalized moving least square reproducing kernel method. J Comput Appl Math, 2013, 249: 120-132 |
| [24] | Liu G, Han X, Lam K Y. A combined genetic algorithm and nonlinear least squares method for material characterization using elastic waves. Comput Methods Appl. Mech Engrg, 2002, 191(17/18): 1909-1921 |
| [25] | Fonken J M, Ramaswamy K R, Paul M J. A scalable multi-step least squares method for network identification with unknown disturbance topology. Automatica, 2022, 141: 110295 |
| [26] | Sun L X, Niu J, Hou J J. A high order convergence collocation method based on the reproducing kernel for general interface problems. Appl Math Lett, 2021, 112: 106718 |
| [27] | Geng F Z, Cui M G. A reproducing kernel method for solving nonlocal fractional boundary value problems. Appl Math Lett, 2012, 25(5): 818-823 |
| [28] | Li X Y, Wu B Y. Error estimation for the reproducing kernel method to solve linear boundary value problems. J Comput Appl Math, 2013, 243: 10-15 |
| [29] | Wu B Y, Li X Y. Application of reproducing kernel method to third order three-point boundary value problems. Appl Math Comput, 2010, 217(7): 3425-3428 |
| [30] | Niu J, Xu M Q, Lin Y Z, Xue Q. Numerical solution of nonlinear singular boundary value problems. J Comput Appl Math, 2018, 331: 42-51 |
| [31] | Xu M Q, Tohidi E, Niu J, Fang Y Z. A new reproducing kernel-based collocation method with optimal convergence rate for some classes of BVPs. Appl Math Comput, 2022, 432: 127343 |
| [32] | Al-Smadia M, Arqub O A, Shawagfeh N, Momanic S. Numerical investigations for systems of second-order periodic boundary value problems using reproducing kernel method. Appl Math Comput, 2016, 291: 137-148 |
| [33] | Niu J, Jia Y T, Sun J D. A new piecewise reproducing kernel function algorithm for solving nonlinear Hamiltonian systems. Appl Math Lett, 2023, 136: 108451 |
| [34] | Xu M Q, Niu J, Lin Y Z. An efficient method for fractional nonlinear differential equations by quasi-Newton's method and simplified reproducing kernel method. Math Methods Appl Sci, 2018, 41(1): 5-14 |
| [35] | Niu J, Sun L X, Xu M Q, Hou J J. A reproducing kernel method for solving heat conduction equations with delay. Appl Math Lett, 2020, 100: 106036 |
| [36] | Niu J, Xu M, Yao G M. An efficient reproducing kernel method for solving the Allen-Cahn equation. Appl Math Lett, 2019, 89: 78-84 |
| [37] | 吴勃英, 林迎珍. 应用型再生核空间. 北京: 科学出版社, 2012 |
| Wu B Y, Lin Y Z. Applied Regenerative Nuclear Space. Beijing: Science Press, 2012 | |
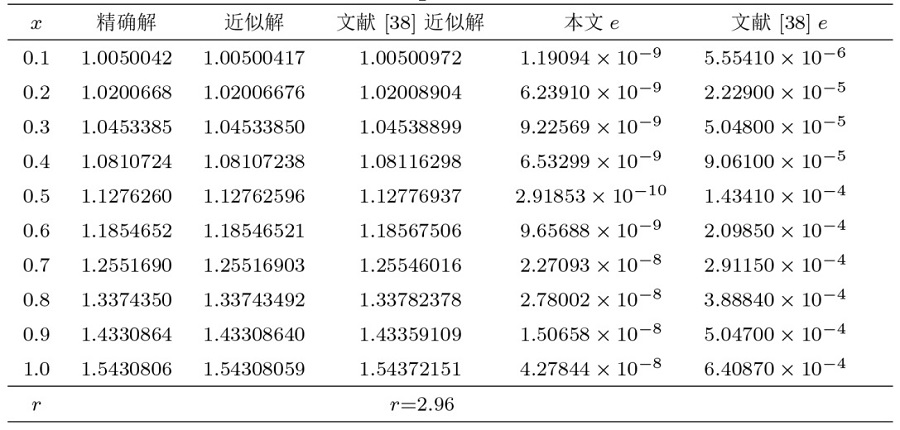
| [38] | Babolian E, Davari A. Numerical implementation of Adomian decomposition method for linear Volterra integral equations of the second kind. Appl Math Comput, 2005, 165(1): 223-27 |
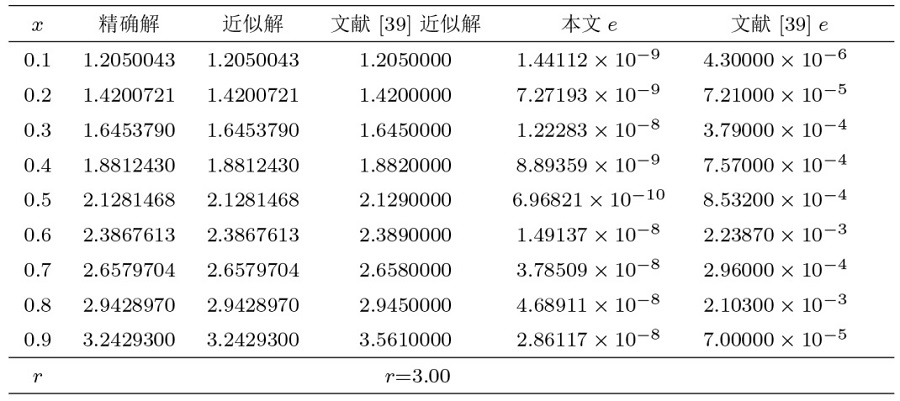
| [39] | Dalal A M. The modified decompositon method for solving Volterra integral equations of the second kind using Maple. Int J GEOMATE, 2019, 17(62): 23-28 |
| [40] | Saad S, Mushtaq A K B. Some new applications of Elzaki transform for solution of linear Volterra type integral equations. J Appl Math Phys, 2019, 7(8): 1877-1892 |
| [41] | Ahmet A. Application of the Bernstein polynomials for solving Volterra integral equations with convolution kernels. Faculty of Sciences and Mathematics, 2016, 30(4): 1045-1052 |
| [42] | Singh I, Kumar S. Haar wavelet method for some nonlinear Volterra integral equations of the first kind. J Comput Appl Math, 2016, 292: 541-552 |
| [43] | Babolian E, Shahsavarani A. Numerical solution of nonlinear Fredholm and Volterra integral equations of the second kind using Haar wavelets and collocation method. J Sci Tarbiat Moallem University, 2007, 7: 213-222 |
| [44] | Mahmoudi Y. Wavelet Galerkin method for numerical solution of nonlinear integral equation. Appl Math Comput, 2005, 167: 1119-1129 |
| [45] | Ishola C Y, Taiwo O A, Adedokun K A, et al. Solution of nonlinear Volterra integral equations by Chebyshev collocation approximation method. Pacific Journal of Science and Technology, 2022, 23(1): 34-39 |
| [1] | 于一康,牛晶. 一类椭圆型界面问题的数值算法[J]. 数学物理学报, 2023, 43(3): 883-895. |
| [2] | 张晶,余旌胡. 线性回归模型参数估计方法的分辨率[J]. 数学物理学报, 2020, 40(5): 1381-1392. |
| [3] | 刘宏影, 吕学琴. 再生核结合配置法求解一类带有积分边值条件的四阶非线性微分方程[J]. 数学物理学报, 2016, 36(5): 928-936. |
| [4] | 周永芳, 崔明根. 一类弱奇异边值问题的大范围收敛算法[J]. 数学物理学报, 2011, 31(1): 142-153. |
| [5] | 吕学琴, 崔明根. 求解奇异三阶边值问题的一个算法[J]. 数学物理学报, 2010, 30(2): 320-326. |
| [6] | 么焕民, 林迎珍. 八阶奇异边值问题精确解的表达形式[J]. 数学物理学报, 2010, 30(1): 103-113. |
| [7] | 杜娟, 崔明根. 再生核空间中求解带有积分边界条件的半线性热传导方程[J]. 数学物理学报, 2010, 30(1): 245-257. |
| [8] | 吕学琴, 崔明根. 在再生核空间中求解非线性奇异两点边值问题[J]. 数学物理学报, 2009, 29(5): 1274-1282. |
| [9] | 李云晖, 崔明根, 刘纯扑. 再生核空间W22(*)中积分-微分方程精确解的表示[J]. 数学物理学报, 1998, 18(S1): 83-92. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 71
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 78
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|