数学物理学报 ›› 2024, Vol. 44 ›› Issue (5): 1302-1310.
PNP 方程的基于高斯过程回归的新 Gummel 迭代算法
- 桂林电子科技大学数学与计算科学学院 & 广西应用数学中心 (GUET) & 广西高校数据分析与计算重点实验室 广西桂林 541004
A New Gummel Iterative Algorithm Based on Gaussian Process Regression for the PNP Equation
- Guilin University of Electronic Technology, School of Mathematics and Computating Science & Guangxi Applied Mathematics Center (GUET) & Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guangxi Guilin 541004
摘要:
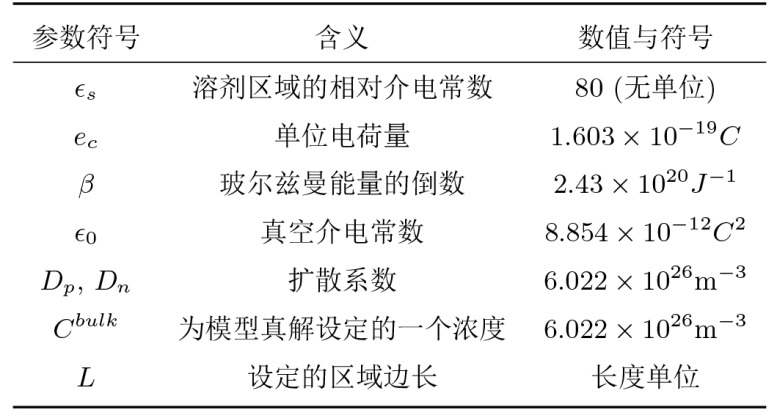
Poisson-Nernst-Planck (PNP) 方程是由 Poisson 方程和 Nernst-Planck 方程耦合而成的一类非线性偏微分方程组, 其常用的线性化迭代方法-Gummel 迭代的效率很大程度上受松弛参数的影响. 机器学习中的高斯过程回归 (GPR) 方法因其训练规模较小, 且不需要提供函数关系, 在该文中被应用于预测 Gummel 迭代的较优松弛参数, 加速迭代的收敛速度. 首先针对 PNP 方程的 Gummel 迭代, 设计了一种可预测松弛参数的 GPR 方法. 其次利用 Box-Cox 转换方法, 对 Gummel 迭代的数据进行预处理, 提高 GPR 方法的准确性. 最后基于 GPR 方法及 Box-Cox 转换算法, 提出了 PNP 方程的一种新的 Gummel 迭代算法. 数值实验表明, 新 Gummel 迭代算法与经典的 Gummel 迭代算法相比, 求解效率更高, 且收敛阶相同.
中图分类号:
- O241.82