数学物理学报 ›› 2023, Vol. 43 ›› Issue (3): 785-794.
聚焦 Kundu-Eckhaus 方程中畸形波的奇异动力学行为研究
- 中国矿业大学数学学院 江苏徐州 221116
-
收稿日期:2022-03-22修回日期:2022-09-22出版日期:2023-06-26发布日期:2023-06-01 -
通讯作者:田守富 E-mail:xbwang@cumt.edu.cn;sftian@cumt.edu.cn -
作者简介:王秀彬,E-mail:xbwang@cumt.edu.cn -
基金资助:国家自然科学基金(12201622);国家自然科学基金(11975306)
Exotic Dynamics of Freak Waves in the Focusing Kundu-Eckhaus Equation
- School of Mathematics, China University of Mining and Technology, Jiangsu Xuzhou 221116
-
Received:2022-03-22Revised:2022-09-22Online:2023-06-26Published:2023-06-01 -
Contact:Shoufu Tian E-mail:xbwang@cumt.edu.cn;sftian@cumt.edu.cn -
Supported by:NSFC(12201622);NSFC(11975306)
摘要:
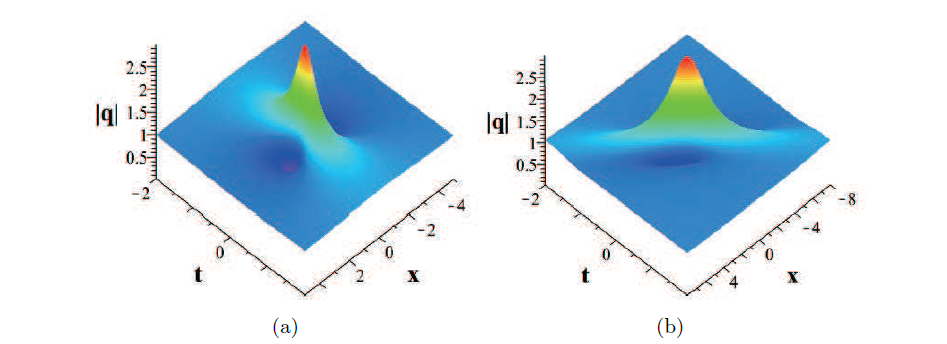
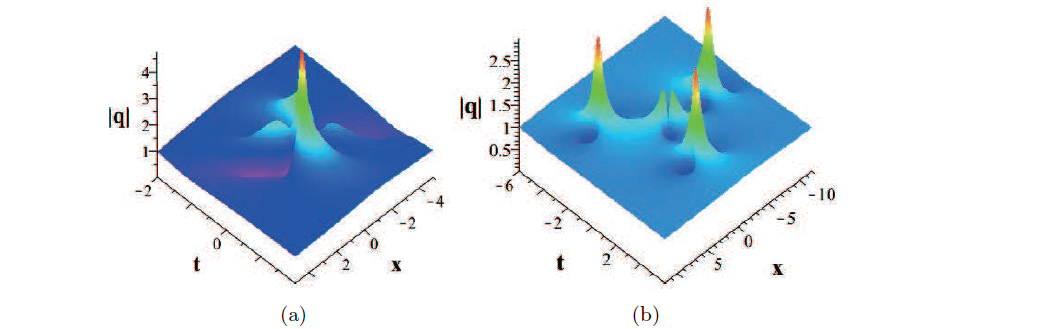
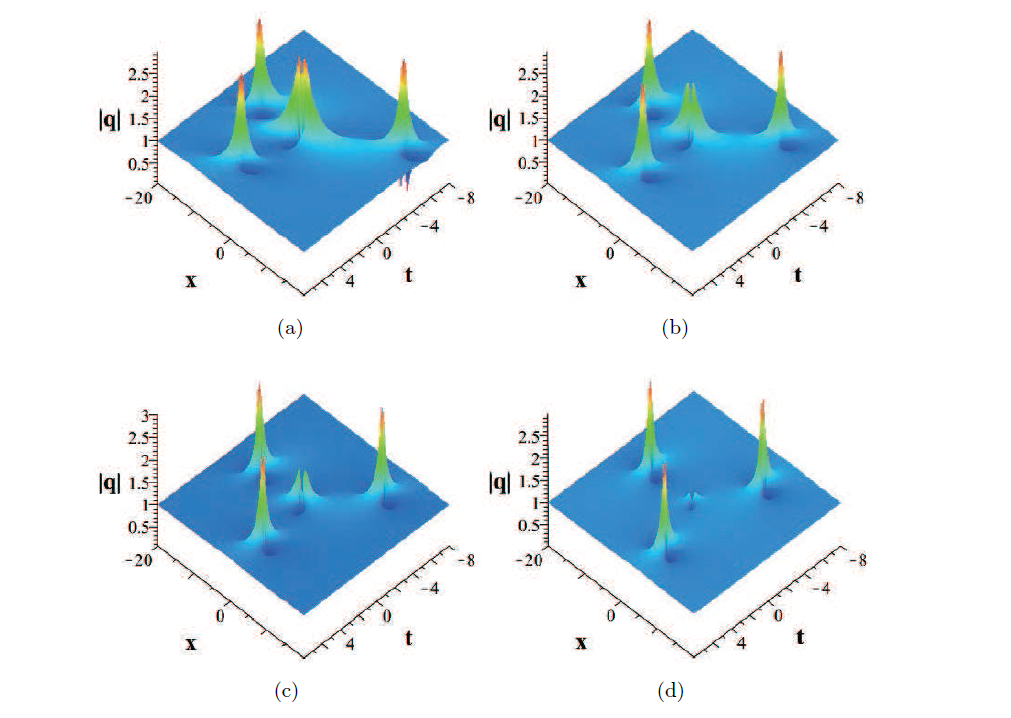
该文基于 Darboux 变换的相关结果, 利用变量分离法推导出了聚焦 Kundu-Eckhaus 方程的一般高阶畸形波解. 然后通过一些图形详细地讨论了这些畸形波解的动力学行为. 特别地, 这里可以观察到一个四瓣形畸形波和三眼形畸形波是可以共存的, 这是完全不同于之前存在的四眼形畸形波. 研究结果表明, 该文所研究的畸形波结构比在著名的非线性 Schrödinger 方程中的畸形波结构更为丰富.
中图分类号:
- O175.2
引用本文
王秀彬, 田守富. 聚焦 Kundu-Eckhaus 方程中畸形波的奇异动力学行为研究[J]. 数学物理学报, 2023, 43(3): 785-794.
Wang Xiubin, Tian Shoufu. Exotic Dynamics of Freak Waves in the Focusing Kundu-Eckhaus Equation[J]. Acta mathematica scientia,Series A, 2023, 43(3): 785-794.
使用本文
| [1] |
Benney B, Newell A C. The propagation of nonlinear wave envelopes. J Math Phys, 1967, 46: 133-139
doi: 10.1002/sapm1967461133 |
| [2] | Ostrowskii L A. Propagation of wave packets and space-time self-focussing in a nonlinear medium. Sov Phys JETP 1967, 24: 797-800 |
| [3] | Sulem C, Sulem P L. The Nonlinear Schrödinger Equation:Self-Focusing and Wave Collapse. New York: Springer, 1999 |
| [4] | Fibich G. The Nonlinear Schrödinger Equation:Singular Solutions and Optical Collapse. New York: Springer, 2015 |
| [5] | Zakharov V E, Shabat A B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov Phys JETP 1972, 34: 62 |
| [6] | Ablowitz M J, Clarkson P A. Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge: Cambridge University Press, 1991 |
| [7] | Matveev V B. Darboux Transformations and Solitons. New York: Springer-Verlag, 1991 |
| [8] |
Ma W X. Darboux transformations for a Lax integrable system in 2n-dimensions. Lett Math Phys 1997, 39: 33-49
doi: 10.1007/s11005-997-3049-3 |
| [9] |
Akhmediev N, Ankiewicz A, Soto-Crespo J M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys Rev E, 2009, 80: 026601
doi: 10.1103/PhysRevE.80.026601 |
| [10] |
Guo B, Ling L, Liu Q P. Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys Rev E, 2012, 85: 026607
doi: 10.1103/PhysRevE.85.026607 |
| [11] |
Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A, 2009, 373: 675-678
doi: 10.1016/j.physleta.2008.12.036 |
| [12] | Kharif C, Pelinovsky E, Slunyaev A. Rogue Waves in the Ocean. Berlin: Springer Science & Business Media, 2008 |
| [13] |
Solli D R, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature, 2007, 450: 1054-1057
doi: 10.1038/nature06402 |
| [14] | Peregrine D. Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc B Appl Math, 1983, 25: 16-43 |
| [15] |
Ankiewicz A, Soto-Crespo J M, Akhmediev N. Discrete rogue waves of the Ablowitz-Ladik and Hirota equations. Phys Rev E, 2010, 81: 046602
doi: 10.1103/PhysRevE.81.046602 |
| [16] |
Guo B L, Ling L M, Liu Q P. High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Stud Appl Math, 2013, 130: 317-344
doi: 10.1111/sapm.2013.130.issue-4 |
| [17] |
Ohta Y, Yang J. Dynamics of rogue waves in the Davey-Stewartson II equation. J Phys A: Math Theor, 2013, 46: 105202
doi: 10.1088/1751-8113/46/10/105202 |
| [18] |
Bandelow U, Akhmediev N. Persistence of rogue waves in extended nonlinear Schrödinger equations: integrable Sasa-Satsuma case. Phys Lett A, 2012, 376: 1558-1561
doi: 10.1016/j.physleta.2012.03.032 |
| [19] |
Mu G, Qin Z, Grimshaw R, Akhmediev N. Intricate dynamics of rogue waves governed by the Sasa-Satsuma equation. Physica D, 2020, 402: 132252
doi: 10.1016/j.physd.2019.132252 |
| [20] |
Baronio F, Degasperis A, Conforti M, Wabnitz S. Solutions of the vector nonlinear Schrödinger equations: evidence for deterministic rogue waves. Phys Rev Lett, 1981, 109: 044102
doi: 10.1103/PhysRevLett.109.044102 |
| [21] |
Mu G, Qin Z, Grimshaw R. Dynamics of rogue waves on a multisoliton background in a vector nonlinear Schrödinger equation. SIAM J Appl Math, 2015, 75: 1-20
doi: 10.1137/140963686 |
| [22] |
Yan Z. Financial rogue waves. Commun Theor Phys, 2010, 54: 947-949
doi: 10.1088/0253-6102/54/5/31 |
| [23] |
Akhmediev N, Korneev V I. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor Math Phys, 1986, 69: 1089
doi: 10.1007/BF01037866 |
| [24] |
Akhmediev N, Ankiewicz A. First-order exact solutions of the nonlinear Schrödinger equation in the normal-dispersion regime. Phys Rev A, 1993, 47: 3213-3221
doi: 10.1103/PhysRevA.47.3213 |
| [25] |
Ohta Y, Yang J. General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc R Soc A, 2012, 468: 1716-1740
doi: 10.1098/rspa.2011.0640 |
| [26] |
Ma W X, Zhou Y. Lump solutionsto nonlinear partial differential equations via Hirota bilinear forms. J Differential Equations, 2018, 264: 2633-2659
doi: 10.1016/j.jde.2017.10.033 |
| [27] |
Wang X B, Tian S F. Exotic vector freak waves in the nonlocal nonlinear Schrödinger equation. Physica D, 2022, 442: 133528
doi: 10.1016/j.physd.2022.133528 |
| [28] |
Tian S F. Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method. J Differential Equations, 2017, 262: 506-558
doi: 10.1016/j.jde.2016.09.033 |
| [29] |
Peng W Q, Pu J C, Chen Y. PINN deep learning method for the Chen-Lee-Liu equation: Rogue wave on the periodic background. Comm Nonlinear Sci Numer Simulat, 2022, 105: 106067
doi: 10.1016/j.cnsns.2021.106067 |
| [30] |
Yang B, Chen Y. Several reverse-time integrable nonlocal nonlinear equations: Rogue-wave solutions. Chaos, 2018, 28: 053104
doi: 10.1063/1.5019754 |
| [31] |
Xu S, He J. The rogue wave and breather solution of the Gerdjikov-Ivanov equation. J Math Phys, 2012, 53: 063507
doi: 10.1063/1.4726510 |
| [32] |
Wang X B, Han B. Vector nonlinear waves in a two-component Bose-Einstein Condensate system. J Phys Soc Jpn, 2020, 89: 124003
doi: 10.7566/JPSJ.89.124003 |
| [33] |
Wang X B, Han B. The three-component coupled nonlinear Schrödinger equation: Rogue waves on a multi-soliton background and dynamics. Europhys Lett, 2018, 126: 15001
doi: 10.1209/0295-5075/126/15001 |
| [34] |
Wang X B, Tian S F, Zhang T T. Characteristics of the breather and rogue waves in a (2+1)-dimensional nonlinear Schrödinger equation. Proc Amer Math Soc, 2018, 146: 3353-3365
doi: 10.1090/proc/2018-146-08 |
| [35] |
Zhaqilao. On Nth-order rogue wave solution to the generalized nonlinear Schrödinger equation. Phys Lett A, 2013, 377: 855-859
doi: 10.1016/j.physleta.2013.01.044 |
| [36] |
Kundu A. Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations. J Math Phys, 1984, 25: 3433
doi: 10.1063/1.526113 |
| [37] |
Kaup D J, Newell A C. An exact solution for a derivative nonlinear Schrödinger equation. J Math Phys, 1978, 19: 798
doi: 10.1063/1.523737 |
| [38] |
Luo J, Fan E. A ˉ∂-dressing approach to the Kundu-Eckhaus equation. J Geom Phys, 2021, 167: 104291
doi: 10.1016/j.geomphys.2021.104291 |
| [39] |
Zhu Q, Xu J, Fan E. The Riemann-Hilbert problem and long-time asymptotics for the Kundu-Eckhaus equation with decaying initial value. Appl Math Lett, 2018, 76: 81-89
doi: 10.1016/j.aml.2017.08.006 |
| [40] |
Wang X B, Han B. A Riemann-Hilbert approachto a generalized nonlinear Schrödinger equationon the quarter plane. Math Phys Anal Geom, 2020, 23: 25
doi: 10.1007/s11040-020-09347-1 |
| [41] |
Wang D S, Guo B L, Wang X L. Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions. J Differential Equations, 2019, 266: 5209-5253
doi: 10.1016/j.jde.2018.10.053 |
| [42] |
Qiu D, He J, Zhang Y, Porsezia K. The Darboux transformation of the Kundu-Eckhaus equation. Proc R Soc A, 2018, 471: 20150236
doi: 10.1098/rspa.2015.0236 |
| [43] |
Wang X, Yang B, Chen Y, Yang T Q. Higher-order rogue wave solutions of the Kundu-Eckhaus equation. Phys Scr, 2014, 89: 095210
doi: 10.1088/0031-8949/89/9/095210 |
| [44] |
Qiu D, Cheng W. The n-fold Darboux transformation for the Kundu-Eckhaus equation and dynamics of the smooth positon solutions. Commun Nonlinear Sci Numer Simulat, 2019, 78: 104887
doi: 10.1016/j.cnsns.2019.104887 |
| [45] |
Bayindir C. Rogue waves of the Kundu-Eckhaus equation in a chaotic wave field. Phys Rev E, 2016, 93: 032201
doi: 10.1103/PhysRevE.93.032201 |
| [46] |
Peng W Q, Tian S F, Zhang T T. Dynamics of breather waves and higher-order rogue waves in a coupled nonlinear Schrödinger equation. Europhys Lett, 2018, 123: 50005
doi: 10.1209/0295-5075/123/50005 |
| [1] | 黎小丽,陈晓莉. 部分耗散的三维Boussinesq方程在静力平衡附近的稳定性和指数衰减[J]. 数学物理学报, 2023, 43(3): 754-770. |
| [2] | 陈淑红,谭忠. 奇异对流方程组非常弱解的梯度正则性[J]. 数学物理学报, 2023, 43(3): 713-732. |
| [3] | 王增桂. 曲率控制细胞和组织生长演化模型的Cauchy问题[J]. 数学物理学报, 2023, 43(3): 771-784. |
| [4] | 李易娴,张正杰. 一类与 Klein-Gordon-Maxwell 问题有关的方程组的基态解的存在性[J]. 数学物理学报, 2023, 43(3): 680-690. |
| [5] | 陈蕊娟, 何映羲, 肖梅霞. 相对论 Nordström-Vlasov 方程解的正则性[J]. 数学物理学报, 2023, 43(3): 743-753. |
| [6] | 邹永辉,徐鑫. 二维可压缩Prandtl方程倒流点的存在性[J]. 数学物理学报, 2023, 43(3): 691-701. |
| [7] | 李敏, 蒲学科. 双流体 Euler-Poisson 方程的长波长极限[J]. 数学物理学报, 2023, 43(2): 399-420. |
| [8] | 熊晨, 高琦. 一类耦合Ginzburg-Landau系统的局部极小解[J]. 数学物理学报, 2023, 43(2): 321-340. |
| [9] | 安雁宁, 刘文军, 孔奥文. 带分数阶磁效应的压电梁在有/无热效应时的稳定性[J]. 数学物理学报, 2023, 43(2): 355-376. |
| [10] | 康笑东, 范虹霞. 一类具有瞬时脉冲的二阶发展方程的近似可控性[J]. 数学物理学报, 2023, 43(2): 421-432. |
| [11] | 曾彪. 一类带有弱连续算子的发展方程的最优控制[J]. 数学物理学报, 2023, 43(2): 515-530. |
| [12] | 张明玉. 输运系数依赖温度的可压缩辐射流体解的整体存在性[J]. 数学物理学报, 2023, 43(2): 458-480. |
| [13] | 陈雪姣, 李远飞, 侯春娟. 半无穷柱体上Forchheimer方程组解的Phragmén-Lindelöf型二择一结果[J]. 数学物理学报, 2023, 43(2): 505-514. |
| [14] | 侍迎春, 赖耕. 球对称 Chaplygin 气体相对论 Euler 方程组的奇性形成[J]. 数学物理学报, 2023, 43(2): 481-490. |
| [15] | 李德科, 王青选. 质量临界非齐次薛定谔方程在门槛值处的极限行为[J]. 数学物理学报, 2023, 43(1): 123-131. |
|