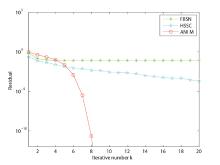
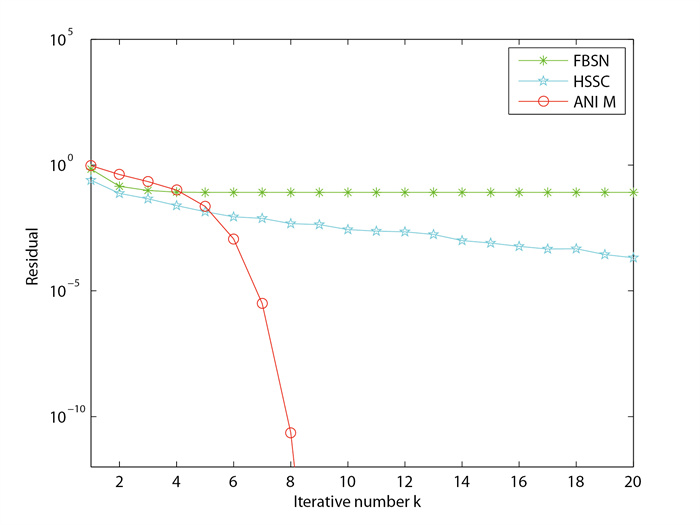
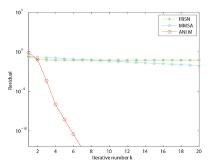
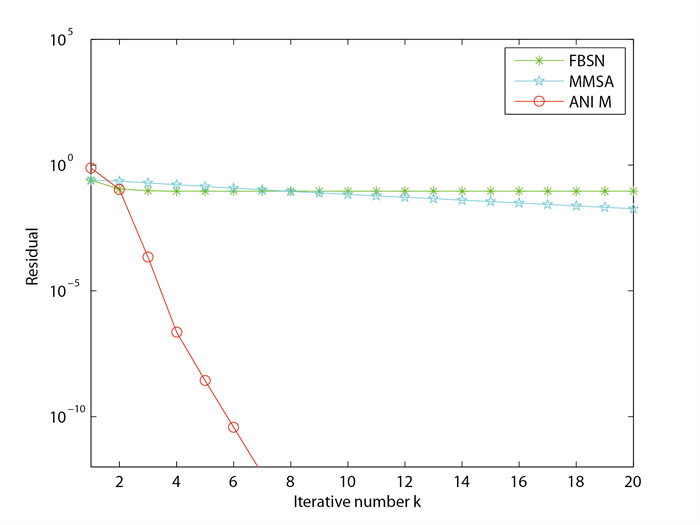
| 1 |
Bai Z Z . Modulus-based matrix splitting iteration methods for linear complementarity problems. Numer Linear Algebra Appl, 2010, 17, 917- 933
doi: 10.1002/nla.680
|
| 2 |
Bai Z Z . On the convergence of the multisplitting methods for the linear complementarity problem. SIAM J Matrix Anal Appl, 1999, 21, 67- 78
doi: 10.1137/S0895479897324032
|
| 3 |
Bai Z Z . Experimental study of the asynchronous multisplitting relaxtation methods for linear complementarity problems. J Comput Math, 2002, 20, 561- 574
|
| 4 |
Bai Z Z , Evans D J . Matrix multisplitting relaxtion methods for linear complementarity problem. Inter J Comput Math, 1997, 63, 309- 326
doi: 10.1080/00207169708804569
|
| 5 |
Bai Z Z , Evans D J . Matrix multisplitting methods with applications to linear complementarity problems: Parallel synchronous and chaotic methods. Calculateurs Parallelés Réseaux et Systémes Répartis, 2001, 13, 125- 154
|
| 6 |
Bai Z Z , Evans D J . Parallel chaotic multisplitting iterative methods for the large spase linear complementarity problem. J Comput Math, 2001, 19, 281- 292
|
| 7 |
Bai Z Z , Evans D J . Matrix multisplitting methods with applications to linear complementarity problems: Parallel asynchronous methods. Int J Comput Math, 2002, 79, 205- 232
doi: 10.1080/00207160211927
|
| 8 |
Bai Z Z , Huang Y G . A class of asynchronous iterations for the linear complementarity problem. J Comput Math, 2003, 21, 773- 790
|
| 9 |
Bai Z Z , Zhang L L . Modulus-based synchronous multisplitting iteration methods for linear complementarity problems. Numer Linear Algebra Appl, 2013, 20, 425- 439
doi: 10.1002/nla.1835
|
| 10 |
Chen X , Nashed Z , Qi L . Smoothing methods and semismooth methods for nondifferentiable operator equations. SIAM J Numer Anal, 2000, 38, 1200- 1216
doi: 10.1137/S0036142999356719
|
| 11 |
Cottle R W , Pang J S , Stone RE . The Linear Complementarity Problem. Boston: Academic Press, 1992
|
| 12 |
Cryer C . The solution of a quadratic programming using systematic overrelaxation. SIAM J Control Optim, 1971, 9, 385- 392
doi: 10.1137/0309028
|
| 13 |
Fischer A . A special Newton-type optimization method. Optim, 1992, 24, 269- 284
doi: 10.1080/02331939208843795
|
| 14 |
Foutayeni Y E L , Khaladi M . Using vector divisions in solving the linear complementarity problem. J Comput Appl Math, 2012, 236, 1919- 1925
doi: 10.1016/j.cam.2011.11.001
|
| 15 |
Huang B H , Xie Y J , Ma C F . Krylov subspace methods to solve a class of tensor equations via the Einstein product. Numer Linear Algebra Appl, 2019, 26 (4): e2254
|
| 16 |
Huang N , Ma C F . The modulus-based matrix splitting algorithms for a class of weakly nonlinear complementarity problems. Numer Linear Algebra Appl, 2016, 23, 558- 569
doi: 10.1002/nla.2039
|
| 17 |
黄象鼎, 曾钟钢, 马亚南. 非线性数值分析的理论与方法. 武汉: 武汉大学出版社, 2004
|
|
Huang X D , Zeng Z G , Ma Y N . The Theory and Methods for Nonlinear Numerical Analysis. Wuhan: University of Wuhan Press, 2004
|
| 18 |
Jiang H Y , Qi L . A new nonsmooth equations approach to nonlinear complementarity problems. SIAM J Control Optim, 1997, 35, 178- 193
doi: 10.1137/S0363012994276494
|
| 19 |
Lemke C E . Bimatrix equilibrium points and mathematical programming. Management Science, 1965, 11 (7): 681- 689
doi: 10.1287/mnsc.11.7.681
|
| 20 |
Luca D , Fancchinei F , Kanzow C . A semismooth equation approach to the solution of nonlinear complementarity problems. Math Program, 1996, 75, 407- 439
|
| 21 |
Murty K G . Linear Complementarity, Linear and Nonlinear Programming. Berlin: Heldermann, 1988
|
| 22 |
Qi L , Sun J . A nonsmooth version of Newtons method. Math Programming, 1993, 58, 353- 367
doi: 10.1007/BF01581275
|
| 23 |
Sun Z , Zeng J P . A monotone semismooth Newton type method for a class of complementarity problems. J Comput Appl Math, 2011, 235, 1261- 1274
doi: 10.1016/j.cam.2010.08.012
|
| 24 |
Tseng P . On linear convergence of iterative method for the variational inequality problem. J Comput Appl Math, 1995, 60, 237- 252
doi: 10.1016/0377-0427(94)00094-H
|
| 25 |
Xie Y J , Ke Y F . Neural network approaches based on new NCP-functions for solving tensor complementarity problem. J Appl Math Comput, 2021, 67, 833- 853
|
| 26 |
Yu Z , Qin Y . A cosh-based smoothing Newton method for P0 nonlinear complementarity problem. Nonlinear Anal, Real World Appl, 2011, 12, 875- 884
|
| 27 |
Zhang L L . Two-step modulus based matrix splitting iteration for linear complementarity problems. Numer Algoritm, 2011, 57, 83- 99
|
| 28 |
Zheng N , Yin J F . Accelerated modulus-based matrix splitting iteration methods for linear complementarity problem. Numer Algoritm, 2011, 57, 83- 99
|