数学物理学报 ›› 2022, Vol. 42 ›› Issue (5): 1517-1536.
求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法
- 重庆师范大学数学科学学院 重庆 401331
-
收稿日期:2021-12-06出版日期:2022-10-26发布日期:2022-09-30 -
通讯作者:彭建文 E-mail:1318286263@qq.com;jwpeng6@aliyun.com -
作者简介:刘丽平, E-mail:1318286263@qq.com -
基金资助:国家自然科学基金面上项目(11171363);重庆英才·创新创业领军人才·创新创业示范团队项目(CQYC20210309536);重庆市高校创新研究群体项目(CXQT20014);重庆市自然科学基金项目(cstc 2021jcyj-msxmX0300)
Modified Subgradient Extragradient Algorithms for Solving Common Elements of Variational Inequality and Fixed Point Problems
- School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331
-
Received:2021-12-06Online:2022-10-26Published:2022-09-30 -
Contact:Jianwen Peng E-mail:1318286263@qq.com;jwpeng6@aliyun.com -
Supported by:the National Natural Science Foundation of China(11171363);the Team Project of Innovation Leading Talent in Chongqing(CQYC20210309536);the Chongqing University Innovation Research Group Project(CXQT20014);the Basic and Advanced Research Project of Chongqing(cstc 2021jcyj-msxmX0300)
摘要:
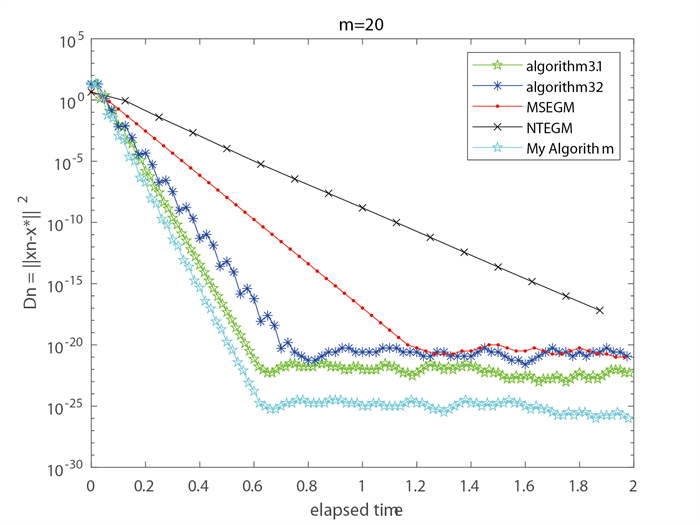
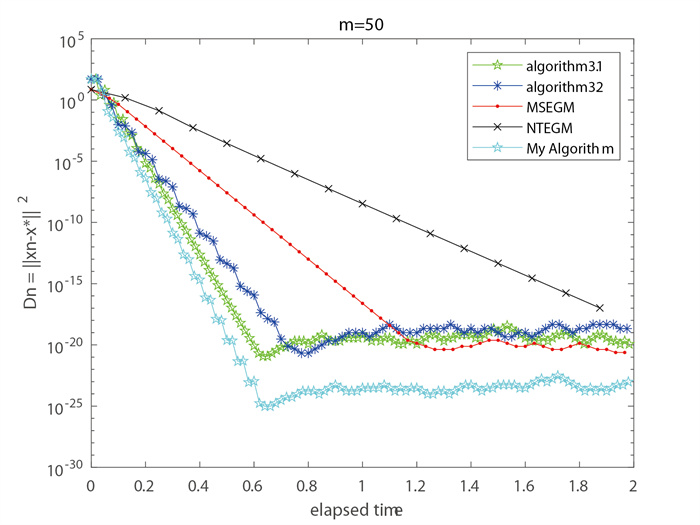
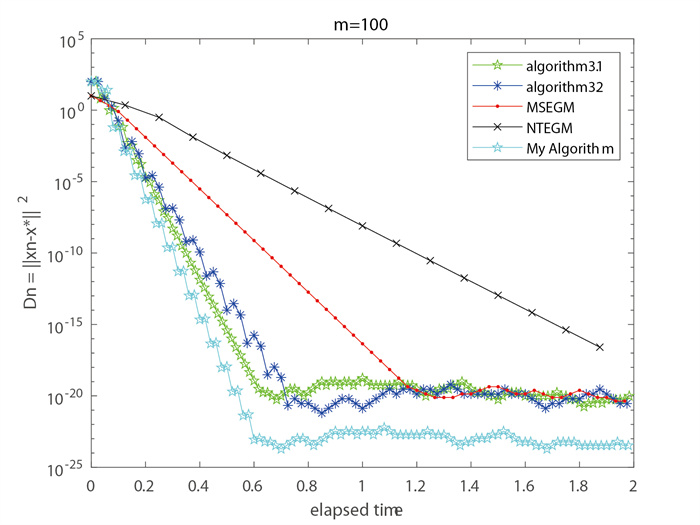
该文在实Hilbert空间中引入了一类新的求解变分不等式问题的惯性次梯度外梯度算法. 在适当的参数假设下, 证明了由该算法所产生的序列强收敛于伪单调变分不等式问题的解集与拟非扩张映射不动点集合的公共元素. 最后, 给出了数值实验来说明所提算法的有效性. 该文所得的结果推广和改进了文献中的一些已有结果.
中图分类号:
- O22
引用本文
刘丽平,彭建文. 求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法[J]. 数学物理学报, 2022, 42(5): 1517-1536.
Liping Liu,Jianwen Peng. Modified Subgradient Extragradient Algorithms for Solving Common Elements of Variational Inequality and Fixed Point Problems[J]. Acta mathematica scientia,Series A, 2022, 42(5): 1517-1536.
使用本文
| 1 | Aubin J P , Ekeland I . Applied Nonlinear Analysis. New York: Wiley, 1984 |
| 2 |
Karamardian S . Complementarity problems over cones with monotone and pseudomonotone maps. J Optim Theory Appl, 1976, 18, 445- 454
doi: 10.1007/BF00932654 |
| 3 | Kinderlehrer D , Stampacchia G . An Introduction to Variational Inequalities and Their Applications. New York: Academic Press, 1980 |
| 4 | Baiocchi C , Capelo A . Variational and Quasivariational Inequalities Applications to Free Boundary Problems. New York: Wiley, 1984 |
| 5 | Konnov I V . Combined Relaxation Methods for Variational Inequalities. Berlin: Springer, 2001 |
| 6 | Sibony M . Methodes iteratives pour les equations et inequations aux derivees partielles non lineares de type monotone. Calcolo, 1970, 7 (1): 65- 183 |
| 7 | Korpelevich G M . The extragradient method for finding saddle points and other problems. Matecon, 1976, 12, 747- 756 |
| 8 |
Cai G , Bu S Q . Modified extragradient methods for variational inequality problems and fixed point problems for an infinite family of nonexpansive mappings in Banach spaces. J Global Optim, 2013, 55 (2): 437- 457
doi: 10.1007/s10898-012-9883-6 |
| 9 |
Cai G , Gibali A , Iyiola O S , Shehu Y . A new double-projection method for solving variational inequalities in Banach spaces. J Optim Theory Appl, 2018, 178, 219- 239
doi: 10.1007/s10957-018-1228-2 |
| 10 |
Iusem A N , Nasri M . Korpelevich's method for variational inequality problems in Banach spaces. J Global Optim, 2011, 50, 59- 76
doi: 10.1007/s10898-010-9613-x |
| 11 |
Yao Y H , Noor M A , Noor K I , Liou Y C , Yaqoob H . Modified extragradient methods for a system of variational inequalities in Banach spaces. Acta Appl Math, 2010, 110, 1211- 1224
doi: 10.1007/s10440-009-9502-9 |
| 12 | Shehu Y . Single projection algorithm for variational inequalities in Banach spaces with application to contact problem. Acta Math Sci, 2020, 40B (4): 1045- 1063 |
| 13 | Popov L D . A modification of the Arrow-Hurwicz method for the search of saddle points. Mathematical notes of the Academy of Sciences of the USSR, 1980, 28, 845- 848 |
| 14 |
Censor Y , Gibali A , Reich S . The subgradient extragradient method for solving variational inequalities in Hilbert space. J Optim Theory Appl, 2011, 148, 318- 335
doi: 10.1007/s10957-010-9757-3 |
| 15 | Ceng L C , Yao J C . Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems. Taiwan J Math, 2006, 10 (5): 1293- 1303 |
| 16 |
Ceng L C , Hadjisavvas N , Wong N C . Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J Global Optim, 2010, 46, 635- 646
doi: 10.1007/s10898-009-9454-7 |
| 17 |
Iiduka H , Takahashi W . Strong convergence theorems for nonexpansive mappings and inverse strongly monotone mappings. Nonlinear Anal, 2005, 61 (3): 341- 350
doi: 10.1016/j.na.2003.07.023 |
| 18 |
Thong D V , Hieu D V . Inertial subgradient extragradient algorithms with line-search process for solving variational inequality problems and fixed point problems. Numer Algor, 2019, 80, 1283- 1307
doi: 10.1007/s11075-018-0527-x |
| 19 |
Cai G , Dong Q L , Peng Y . Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators. J Optim Theory Appl, 2021, 188, 447- 472
doi: 10.1007/s10957-020-01792-w |
| 20 |
Yang H , Agarwal R P , Nashine H K , Liang Y . Fixed point theorems in partially ordered Banach spaces with applications to nonlinear fractional evolution equations. J Fixed Point Theory Appl, 2017, 19, 1661- 1678
doi: 10.1007/s11784-016-0316-x |
| 21 |
Takahashi W , Toyoda M . Weak convergence theorems for nonexpansive mappings and monotone mappings. J Optim Theory Appl, 2003, 118, 417- 428
doi: 10.1023/A:1025407607560 |
| 22 |
Nadezhkina N , Takahashi W . Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. J Optim Theory Appl, 2006, 128, 191- 201
doi: 10.1007/s10957-005-7564-z |
| 23 | Diaz J B , Metcalf F T . Subsequential limit points of successive approximations. Trans Amer Math Soc, 1969, 135, 459- 485 |
| 24 |
Thong D V , Li X H , Dong Q L , Cho Y J , Rassias T M . An inertial Popov's method for solving pseudomonotone variational inequalities. Optim Lett, 2021, 15, 757- 777
doi: 10.1007/s11590-020-01599-8 |
| 25 |
Bot R I , Csetnek E R . An inertial Tseng's type proximal algorithm for nonsmooth and nonconvex optimization problems. J Optim Theory Appl, 2016, 171, 600- 616
doi: 10.1007/s10957-015-0730-z |
| 26 |
贺月红, 龙宪军. 求解伪单调变分不等式问题的惯性收缩投影算法. 数学物理学报, 2021, 41A (6): 1897- 1911
doi: 10.3969/j.issn.1003-3998.2021.06.026 |
|
He Y H , Long X J . An inertial contraction and projection algorithm for pseudomonotone variational inequality problems. Acta Math Sci, 2021, 41A (6): 1897- 1911
doi: 10.3969/j.issn.1003-3998.2021.06.026 |
|
| 27 |
Dong Q L , Yuan H B , Cho Y J , Rassias T M . Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim Lett, 2018, 12, 87- 102
doi: 10.1007/s11590-016-1102-9 |
| 28 |
Thong D V , Hieu D V . An inertial method for solving split common fixed point problems. J Fixed Point Theory Appl, 2017, 19, 3029- 3051
doi: 10.1007/s11784-017-0464-7 |
| 29 | Goebel K , Reich S . Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. New York: Marcel Dekker, 1984 |
| 30 |
Cottle R W , Yao J C . Pseudo-monotone complementarity problems in Hilbert space. J Optim Theory Appl, 1992, 75, 281- 295
doi: 10.1007/BF00941468 |
| 31 |
Xu H K . Iterative algorithm for nonlinear operators. Journal of the London Mathematical Society, 2002, 66 (1): 240- 256
doi: 10.1112/S0024610702003332 |
| 32 |
Mainge P E . The viscosity approximation process for quasi-nonexpansive mapping in Hilbert space. Computers and Mathematics with Applications, 2010, 59, 74- 79
doi: 10.1016/j.camwa.2009.09.003 |
| 33 |
Denisov S V , Semenov V V , Chabak L M . Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators. Cybern Syst Anal, 2015, 51, 757- 765
doi: 10.1007/s10559-015-9768-z |
| 34 |
Iusem A N , Otero R G . Inexact versions of proximal point and augmented Lagrangian algorithms in Banach spaces. Numer Funct Anal Optim, 2001, 22, 609- 640
doi: 10.1081/NFA-100105310 |
| 35 |
Yang J . Self-adaptive inertial subgradient extragradient algorithm for solving pseudomonotone variational inequalities. Applicable Analysis, 2021, 100 (5): 1067- 1078
doi: 10.1080/00036811.2019.1634257 |
| 36 | Harker P T , Pang J S . A damped-Newton method for the linear complementarity problem. Lect Appl Math, 1990, 26, 265- 284 |
| 37 |
Solodov M V , Svaiter B F . A new projection method for variational inequality problems. SIAM J Control Optim, 1999, 37 (3): 765- 776
doi: 10.1137/S0363012997317475 |
| [1] | 施翠云,宾茂君. Banach空间中微分变分不等式系统的Bang-Bang准则[J]. 数学物理学报, 2022, 42(6): 1653-1670. |
| [2] | 刘文杰,谢胜利. 脉冲无穷时滞中立型测度微分方程mild解的存在性[J]. 数学物理学报, 2022, 42(6): 1671-1681. |
| [3] | 杨静,龙宪军. 关于伪单调变分不等式与不动点问题的新投影算法[J]. 数学物理学报, 2022, 42(3): 904-919. |
| [4] | 段磊,陈天兰. 带平均曲率算子的离散混合边值问题凸解的存在性[J]. 数学物理学报, 2022, 42(2): 379-386. |
| [5] | 赵童,袁海龙,郭改慧. 一类具有修正的Leslie-Gower项的捕食-食饵模型的正解[J]. 数学物理学报, 2022, 42(1): 176-186. |
| [6] | 韩晓玲,蔡蕙泽,杨虎军. 星图上非线性分数阶微分方程边值问题解的存在唯一性[J]. 数学物理学报, 2022, 42(1): 139-156. |
| [7] | 贺月红,龙宪军. 求解伪单调变分不等式问题的惯性收缩投影算法[J]. 数学物理学报, 2021, 41(6): 1897-1911. |
| [8] | 张纪凤,张伟,倪晋波,任丹丹. 带p(t)-Laplacian算子的分数阶Langevin方程反周期边值问题解的存在性[J]. 数学物理学报, 2021, 41(4): 1024-1032. |
| [9] | 徐家发,罗洪林,刘立山. 一类具有p-Laplacian算子的分数阶差分方程边值问题的正解[J]. 数学物理学报, 2021, 41(2): 402-414. |
| [10] | 梁载涛,单雪梦. |
| [11] | 万升联. 解变分不等式的一种二次投影算法[J]. 数学物理学报, 2021, 41(1): 237-244. |
| [12] | 何泽荣,张智强,王阳. 一类非线性年龄等级结构种群模型的稳定性[J]. 数学物理学报, 2020, 40(6): 1712-1722. |
| [13] | 李海侠. 一类具有毒素的非均匀chemostat模型正解的存在性和唯一性[J]. 数学物理学报, 2020, 40(5): 1175-1185. |
| [14] | 史平. 一类抽象二元非线性算子的不动点的存在性与唯一性[J]. 数学物理学报, 2020, 40(4): 882-890. |
| [15] | 蔡钢. Hilbert空间中关于变分不等式问题和不动点问题的粘性隐式中点算法[J]. 数学物理学报, 2020, 40(2): 395-407. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 155
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 116
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|