数学物理学报(英文版) ›› 2024, Vol. 44 ›› Issue (5): 1965-1983.doi: 10.1007/s10473-024-0520-5
A SINGULAR DIRICHLET PROBLEM FOR THE MONGE-AMPÈRE TYPE EQUATION*
Zhijun Zhang†, Bo Zhang
- School of Mathematics and Information Science, Yantai University, Yantai 264005, China
-
收稿日期:2022-08-23修回日期:2024-05-16出版日期:2024-10-25发布日期:2024-10-22 -
通讯作者:†Zhijun Zhang, E-mail,:zhangzj@ytu.edu.cn -
作者简介:Bo Zhang, E-mail,: 329175332@qq.com -
基金资助:Zhijun Zhang's research was supported by Shandong Provincial NSF (ZR2022MA020).
A SINGULAR DIRICHLET PROBLEM FOR THE MONGE-AMPÈRE TYPE EQUATION*
Zhijun Zhang†, Bo Zhang
- School of Mathematics and Information Science, Yantai University, Yantai 264005, China
-
Received:2022-08-23Revised:2024-05-16Online:2024-10-25Published:2024-10-22 -
Contact:†Zhijun Zhang, E-mail,:zhangzj@ytu.edu.cn -
About author:Bo Zhang, E-mail,: 329175332@qq.com -
Supported by:Zhijun Zhang's research was supported by Shandong Provincial NSF (ZR2022MA020).
摘要: We consider the singular Dirichlet problem for the Monge-Ampère type equation 

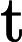






























































































中图分类号:
- 35J60
引用本文
Zhijun Zhang, Bo Zhang. A SINGULAR DIRICHLET PROBLEM FOR THE MONGE-AMPÈRE TYPE EQUATION*[J]. 数学物理学报(英文版), 2024, 44(5): 1965-1983.
Zhijun Zhang, Bo Zhang. A SINGULAR DIRICHLET PROBLEM FOR THE MONGE-AMPÈRE TYPE EQUATION*[J]. Acta mathematica scientia,Series B, 2024, 44(5): 1965-1983.
使用本文
| [1] Bingham N H, Goldie C M, Teugels J L. Regular Variation, Encyclopedia of Mathematics and its Applications. Cambridgeshire: Cambridge University Press, 1987 [2] Caffarelli L, Nirenberg L, Spruck J. The Dirichlet problem for nonlinear second-order elliptic equations, I. Monge-Ampère equation. Comm Pure Appl Math, 1984, 37: 369-402 [3] Calabi E. Complete affine hypersurfaces I. Symposia Math, 1972, 10: 19-38 [4] Chen H D, Huang G G. Existence and regularity of the solutions of some singular Monge-Ampère equations. J Diff Equations, 2019, 267: 866-878 [5] Cheng S Y, Yau S-T. On the regularity of the Monge-Ampère equation det                      [6] Cheng S Y, Yau S-T. Complete affine hypersurfaces I: The completeness of affine metrics. Comm Pure Appl Math, 1986, 39: 839-866 [7] Cîrstea F C, Trombetti C. On the Monge-Ampère equation with boundary blow-up: existence,uniqueness and asymptotics. Cal Var Partial Diff Equations, 2008, 31: 167-186 [8] Cui F, Jian H Y, Li Y. Boundary Hölder estimates for nonlinear singular elliptic equations. J Math Anal Appl, 2019, 470: 1185-1193 [9] Figalli A.The Monge-Ampère Equation and Its Applications. Zurich Lectures in Advanced Mathematics. Zurich: European Mathematical Society, 2017 [10] Gilbarg D, Trudinger N.Elliptic Partial Differential Equations of Second Order. 3rd ed. Berlin: Springer-Verlag, 1998 [11] Guan B, Jian H Y. The Monge-Ampère equation with infinite boundary value. Pacific J Math, 2004, 216: 77-94 [12] Jian H Y, Wang X J. Optimal boundary regularity for nonlinear singular elliptic equations. Adv Math, 2014, 251: 111-126 [13] Jian H Y, Wang X J, Zhao Y. Global smoothness for a singular Monge-Ampère equation. J Diff Equations, 2017, 263: 7250-7262 [14] Jian H Y, Li Y. Optimal boundary regularity for a singular Monge-Ampère equation. J Diff Equations, 2018, 264: 6873-6890 [15] Lazer A C, McKenna P J. On singular boundary value problems for the Monge-Ampère operator. J Math Anal Appl, 1996, 197: 341-362 [16] Le N Q. Optimal boundary regularity for some singular Monge-Ampère equations on bounded convex domains. Discrete Continuous Dynamical Systems, 2022, 42: 2199-2214 [17] Li D S, Ma S S. Existence and boundary behavior of solutions of Hessian equations with singular right-hand sides. J Funct Anal, 2019, 276: 2969-2989 [18] Li M N, Li Y. Global regularity for a class of Monge-Ampère type equations. Science China Math, 2022, 65: 501-516 [19] Lin F H, Wang L H. A class of fully nonlinear elliptic equations with singularity at the boundary. J Geom Anal1998, 8: 583-598 [20] Lions P L. Sur les équations de Monge-Ampère. Arch Rational Mech Anal, 1985, 89: 93-122 [21] Maric V.Regular Variation and Differential Equations. Berlin: Springer-Verlag, 2000 [22] Mohammed A. Existence and estimates of solutions to a singular Dirichlet problem for the Monge-Ampère equation. J Math Anal Appl, 2008, 340: 1226-1234 [23] Mohammed A. Singular boundary value problems for the Monge-Ampère equation. Nonlinear Anal, 2009, 70: 457-464 [24] Nirenberg L. Monge-Ampère equations associated with problems in geometry// Proc Internat Congress of Mathematicians, vol 2.Vancouver, 1974: 275-279 [25] Seneta R. Regular Varying Functions.Berlin: Springer-Verlag, 1976 [26] Sun H Y, Feng M Q. Boundary behavior of   [27] Tian G. On the existence of solutions of a class of Monge-Ampère equations. Acta Mathematica Sinica, New Series, 1988,4: 250-265 [28] Urbas J I E. Global Hölder estimates for equations of Monge-Ampère type. Invent Math, 1988, 91: 1-29 [29] Wan H T, Shi Y X, Liu W. Refined second boundary behavior of the unique strictly convex solution to a singular Monge-Ampère equation. Adv Nonlinear Anal, 2022, 11: 321-356 [30] Zhang Z J. Refined boundary behavior of the unique convex solution to a singular Dirichlet problem for the Monge-Ampère equation. Adv Nonlinear Studies, 2018, 18: 289-302 [31] Zhang Z J. Optimal global asymptotic behavior of the solution to a singular Monge-Ampère equation. Comm Pure Appl Anal, 2020, 19: 1129-1145 [32] Zhang Z J. Optimal global and boundary asymptotic behavior of large solutions to the Monge-Ampère equation. J Funct Anal, 2020, 278: Art 108512 |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 2
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 51
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|
