Complex dynamics of a predator-prey system with herd and schooling behavior: with or without delay and diffusion
1
2021
... 生态系统的生物动力学, 包括空间扩散的机制和模式, 是当前生物数学研究的热点. 一般来说, 种群间相互作用的系统有三类, 包括互惠系统、竞争系统和捕食者--猎物系统[1]. 在这些系统中, 捕食者--猎物系统是最受关注的系统, 并受到了广泛的研究. 随着反应扩散方程理论的发展, 许多学者提出了各种种群生态学机制来更准确地描述捕食者和猎物之间的关系. 特别是恐惧效应和集群行为, 使物种的动力学行为更加真实. ...
Perceived predation risk reduces the number of offspring songbirds produce per year
2
2011
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
... [2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
Fear of large carnivores causes a trophic cascade
1
2016
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
Increased perception of predation risk to adults and offspring alters avian reproductive strategy and performance
1
2014
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
A comparison of shark and wolf research reveals similar behavioral responses by prey
1
2011
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
Fear effects associated with predator presence and habitat structure interact to alter herbivory on coral reefs
1
2019
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
Modelling the fear effect in predator-prey interactions
1
2016
... 最近, 一些研究人员发现, 捕食者的存在可能会改变猎物的生理和行为. 也就是说,捕食者的存在比直接捕食对猎物的影响更大[2⇓⇓⇓-6].Zanette 等[2]进行了一项实验, 以测试感知到的捕食风险是否会单独影响歌雀的繁殖习性. 他们发现恐惧因素降低了猎物的存活率和出生率. 后来, Wang等[7]通过一个具体的数学模型刻画了恐惧效应在捕食者--猎物系统中的作用, 即 ...
Population dynamics with multiple Allee effects induced by fear factors-A mathematical study on prey-predator interactions
1
2018
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Delay induced multiple stability switch and chaos in a predator-prey model with fear effect
1
2020
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge
1
2019
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Fear-driven extinction and (de) stabilization in a predator-prey model incorporating prey herd behavior and mutual interference
1
2023
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Turing-Hopf bifurcation of a delayed diffusive predator-prey system with chemotaxis and fear effect
1
2021
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Spatiotemporal dynamics of a delayed diffusive ratio-dependent predator-prey model with fear effect
1
2021
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Modeling the fear effect and stability of non-equilibrium patterns in mutually interfering predator-prey systems
1
2020
... 其中 u 和 v 分别表示猎物和捕食者的数量. r 和 d 分别表示猎物的出生率和自然死亡率. A 代表种内竞争, e 和 C 分别是生物转化率和死亡率. h(u,v) 代表功能反应. \frac{ru}{1+kv} 反映了恐惧对猎物出生率的影响, 恐惧程度为 k. 此外, 他们研究了 h(u,v) 为 Holling Ⅰ 或Ⅱ型的情况, 发现恐惧因素影响系统 (1.1) 的 Hopf 分支方向. 此后, 越来越多的学者开始研究具有恐惧效应的捕食者-猎物系统. Sasmal[8] 研究了一个具有恐惧因子诱导 Allee 效应的捕食者--猎物模型. Panday 等[9]在捕食者--猎物模型中考虑了时滞型的恐惧效应. Wang 等[10]考虑了一个包含恐惧效应和猎物庇护的捕食者--猎物系统. Antwi-Fordjour 等[11]研究了恐惧如何影响相互干扰的系统的动力学. Dai 和 Sun[12]研究了具有恐惧效应和趋食性的时滞型扩散捕食者--猎物系统的 Turing-Hopf 分支. Zhang 等[13]研究了具有恐惧效应的比例依赖型的扩散捕食者--猎物系统的时空动力学. Tiwari 等[14]详细讨论了恐惧水平和相互干扰对 Turing 斑图和捕食者--猎物系统稳定性的影响. ...
Predator-prey interactions in two schooling fishes, caranx ignobilis and stolephorus purpureus
1
1978
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
Group hunting behaviour of lions: a search for cooperation
1
1991
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
Modeling herd behavior in population systems
1
2011
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
Global dynamics of a predator-prey model with defense mechanism for prey
1
2016
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
Analysis of a predator-prey model for exploited fish populations with schooling behavior
2
2018
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
... 其中 B 和 K 分别为搜索效率和最大环境承载力. Manna 等[19]将线性收获率纳入猎物和捕食者, 研究了动态最优和最优收获策略. Melchionda 等[20]研究了系统 (1.2) 对应的竞争模型的极限环和 Hopf 分支. 后来, Jiang[21]在系统 (1.2) 中考虑空间扩散, 研究了相应的 Turing 分支, 模型如下 ...
Social behavior-induced multistability in minimal competitive ecosystems
2
2017
... 此外, 种群的集群行为是生态系统中的一个重要现象, 参见文献 [15,16]. 集群行为有助于猎物提高生存能力, 同时也能使捕食者更有效地捕猎. 对于猎物的集群行为, Ajraldi 等[17]提出了一个平方根反应函数, 并且平方根作用于猎物. Xu 等[18]研究了具有群体防御的捕食者--猎物系统的全局动力学. 对于捕食者的集群行为, Manna 等[19]和 Melchionda 等[20]提出了作用于捕食者的平方根反应函数. 即建立的模型如下 ...
... 其中 B 和 K 分别为搜索效率和最大环境承载力. Manna 等[19]将线性收获率纳入猎物和捕食者, 研究了动态最优和最优收获策略. Melchionda 等[20]研究了系统 (1.2) 对应的竞争模型的极限环和 Hopf 分支. 后来, Jiang[21]在系统 (1.2) 中考虑空间扩散, 研究了相应的 Turing 分支, 模型如下 ...
Turing bifurcation in a diffusive predator-prey model with schooling behavior
1
2019
... 其中 B 和 K 分别为搜索效率和最大环境承载力. Manna 等[19]将线性收获率纳入猎物和捕食者, 研究了动态最优和最优收获策略. Melchionda 等[20]研究了系统 (1.2) 对应的竞争模型的极限环和 Hopf 分支. 后来, Jiang[21]在系统 (1.2) 中考虑空间扩散, 研究了相应的 Turing 分支, 模型如下 ...
Turing pattern induced by cross-diffusion in a predator-prey model with pack predation-herd behavior
1
2020
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Turing patterns induced by self-diffusion in a predator-prey model with schooling behavior in predator and prey
1
2021
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Diffusion, self-diffusion and cross-diffusion
1
1996
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Pattern formation in a cross-diffusion system
1
2015
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Dynamics of virus infection models with density-dependent diffusion
1
2017
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Analysis of nonautonomous predator-prey model with nonlinear diffusion and time delay
1
2008
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
The linear and nonlinear diffusion of the competitive Lotka-Volterra model
1
2007
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems
1
2016
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Bifurcation analysis and Turing instability in a diffusive predator-prey model with herd behavior and hyperbolic mortality
1
2015
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system
1
2009
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Diffusive spatial movement with memory
1
2020
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system
1
2021
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Spatial movement with diffusion and memory-based self-diffusion and cross-diffusion
1
2021
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay
1
2019
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Hopf bifurcation in a delayed reaction-diffusion-advection population model
1
2018
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Spatiotemporal dynamics of a diffusive predator-prey system with Allee effect and threshold hunting
1
2020
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Global dynamics of a classical Lotka-Volterra competition-diffusion-advection system
1
2018
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Spatiotemporal patterns induced by Turing and Turing-Hopf bifurcations in a predator-prey system
1
2020
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
Global bifurcation and pattern formation for a reaction-diffusion predator-prey model with prey-taxis and double Beddington-DeAngelis functional responses
1
2022
... 其中 D_{1} 和 D_{2} 表示扩散系数, \Delta 是拉普拉斯算子. Yang 等[22]推导了具有交叉扩散的系统 (1.3) 发生 Turing 不稳定性的条件, 得到了系统的多种斑图. Zhou 等[23]通过推导振幅方程研究了自扩散系统 (1.3) 的稳定性和斑图类型. 实际上, 具有扩散的捕食者--猎物系统已经得到了大量的研究. 而且交叉扩散、自扩散和扩散三者是有区别的[24,25]. Wang 等[26]研究了一个密度依赖型扩散的系统. 非线性扩散的系统也有学者研究[27,28]. Wang 等[29]研究了扩散的捕食者--猎物系统中的斑图和全局分支. Tang 和 Song[30]考虑了一个只有猎物具有集群行为的扩散捕食者--猎物模型, 研究了 Turing 不稳定性和 Hopf 分支. Yi 等[31]分析了一类扩散的捕食者--猎物系统的斑图和分支. Shi 等[32]研究了空间运动与记忆的关系.Song 等[33]研究了基于记忆的扩散系统中记忆时滞引起的 Hopf 分支. Shi 等[34]考虑了动物运动建模中的空间记忆. Jiang 等[35]考虑了扩散的 Schnakenberg 系统的 Turing-Hopf 分支. Chen 等[36]考虑了一个扩散模型中由时滞引起的 Hopf 分支问题. Wu 和 Zhao[37]分析了阈值狩猎引起的动力学分类. Zhou 和 Xiao[38]研究了一个竞争--扩散--对流系统. Chen 和 Wu[39]分析了一个扩散模型中的 Turing 斑图. Luo 和Wang[40]研究了一个扩散模型中猎物趋食性对稳定性的影响. ...
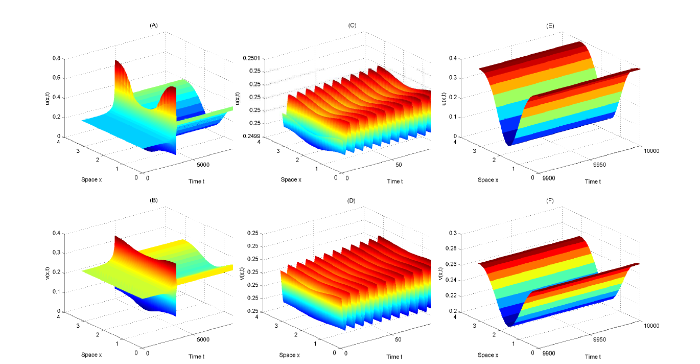
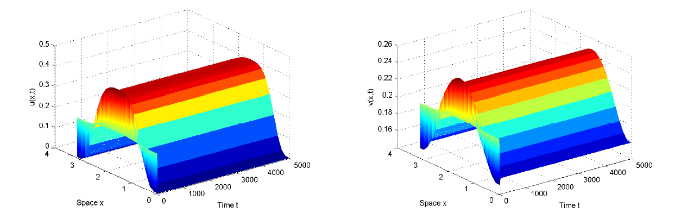
Turing-Hopf bifurcation in the reaction-diffusion equations and its applications
3
2016
... 为了研究系统 (1.5) 在 Turing-Hopf 分支点附近的动力学分类, 我们利用 Song 等[41]的方法来计算相应的规范型. 设 \epsilon_{1}=d_{1} -d^{*}_{1},\epsilon_{2}=\sigma -\sigma^{*}, 引入扰动参数 (\epsilon_{1},\epsilon_{2}). 将 E_{*}(u_{*},v_{*}) 改写为 E_{*}(u_{*}(\epsilon),v_{*}(\epsilon)), 即 ...
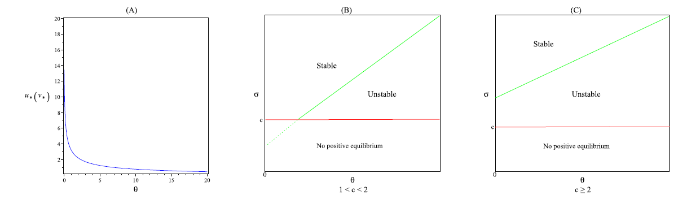
... 其中 \omega_{0}=\sqrt{\frac{(c-1)(1+(2c-1)\theta)}{2(2+(c-1)\theta)}}.利用 Song 等[41]的方法, 我们得到下列在 Turing-Hopf 分支点 (\sigma^{*},d^{*}_{1}) 处的规范型 ...
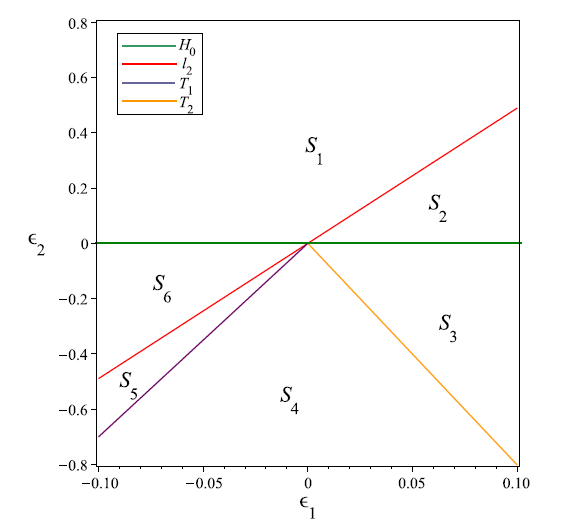
... 以上四条直线将 \epsilon_{1}-\epsilon_{2} 平面分成六个部分, 用 S_{i} \ (i=1,\cdots,6) 标记, 如图2 所示. 由文献 [41] 可知, (5.3) 式中的 A_{0}, \ A_{1}, \ A^{\pm}_{2}, \ A^{\pm}_{3} 分别对应了以下不同的解 ...