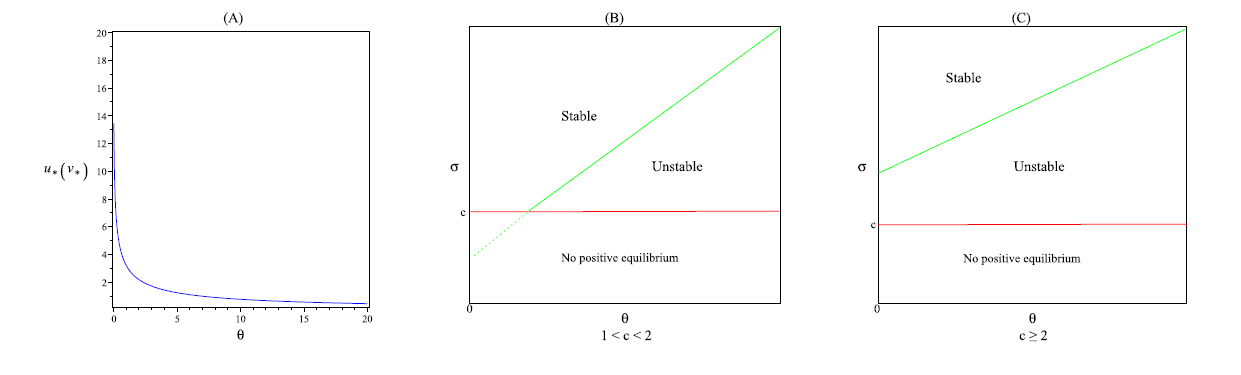
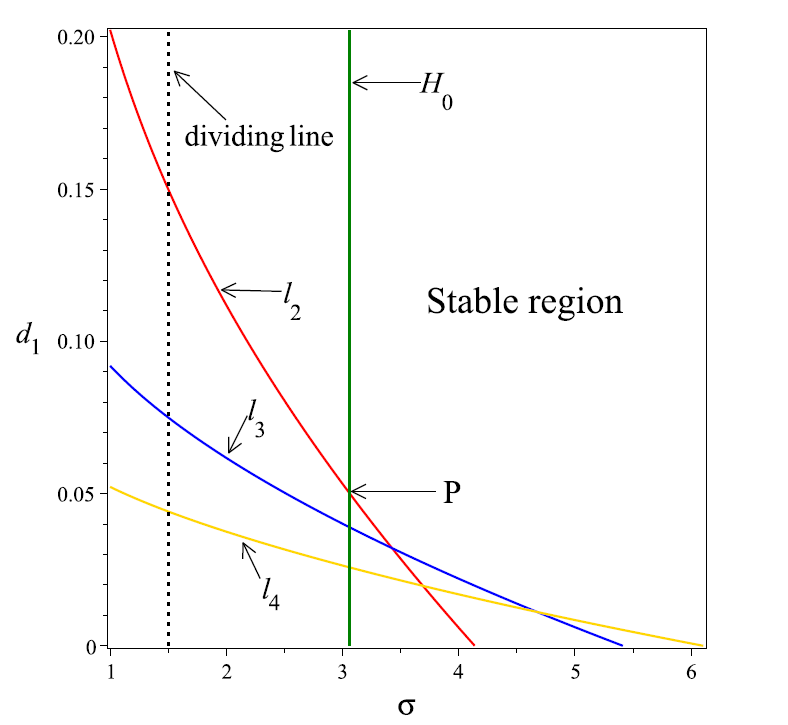
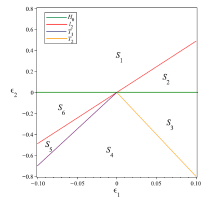
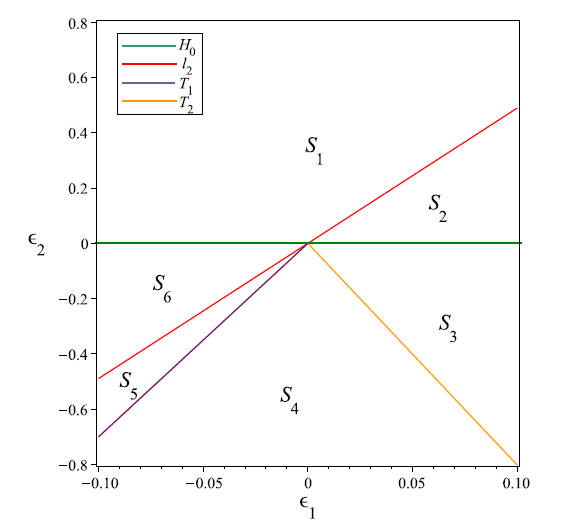
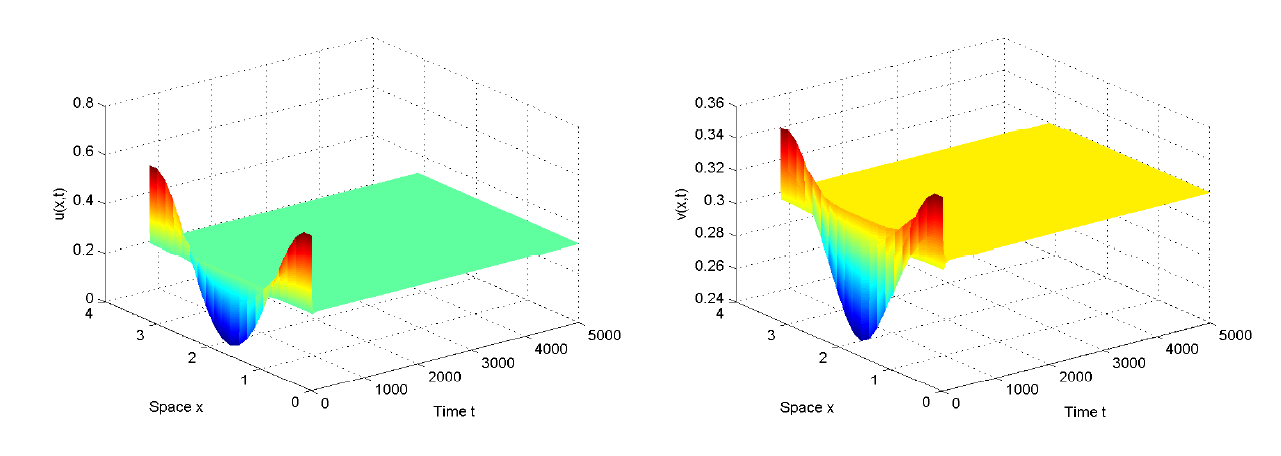
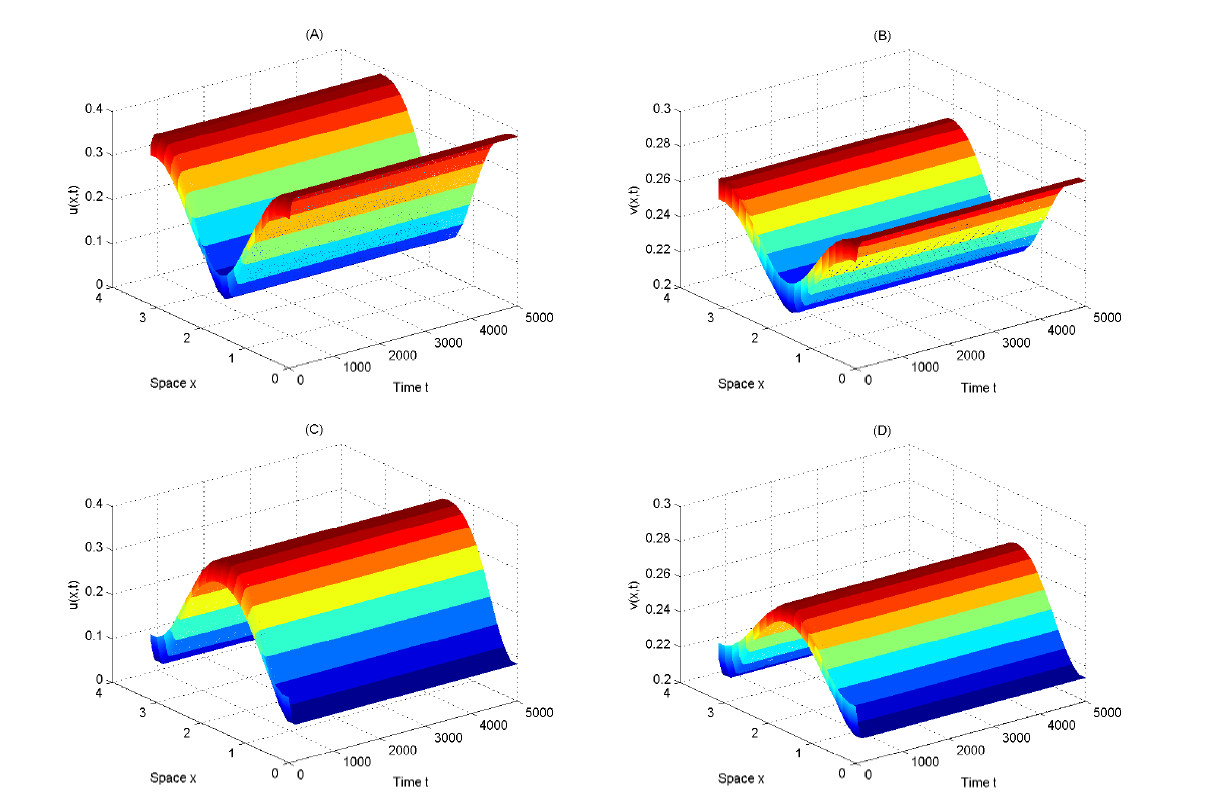
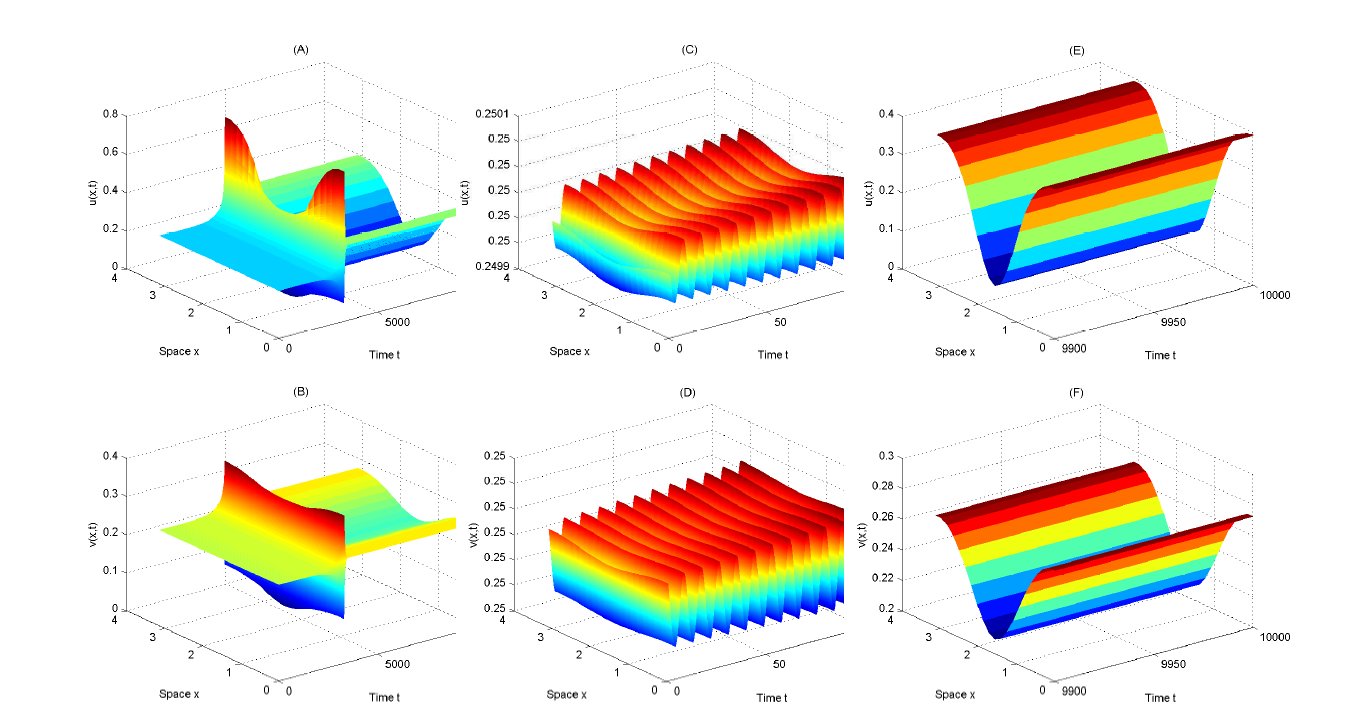
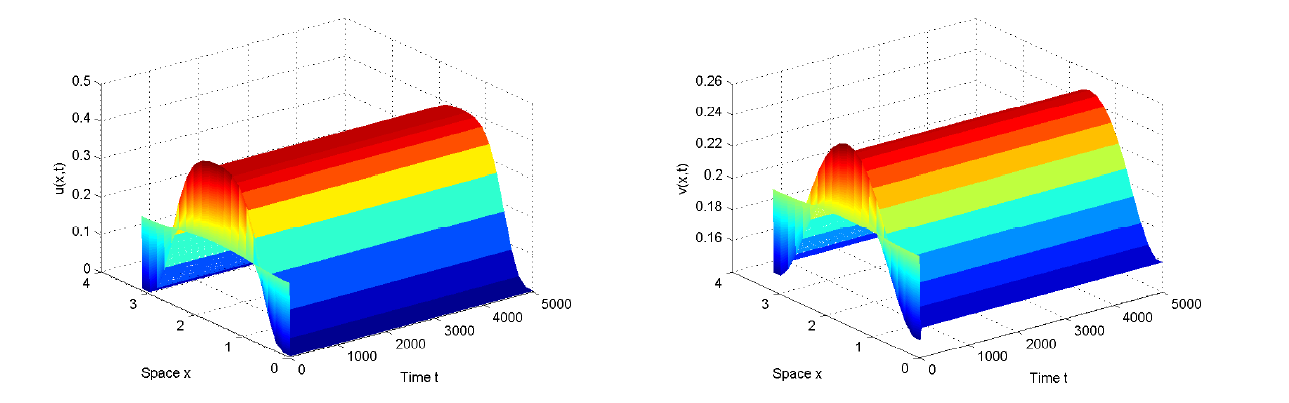
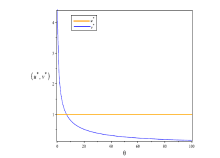
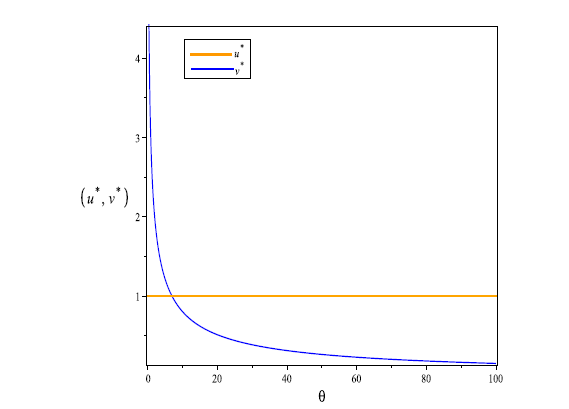
| [1] |
Yang J, Yuan S, Zhang T. Complex dynamics of a predator-prey system with herd and schooling behavior: with or without delay and diffusion. Nonlinear Dyn, 2021, 104: 1709-1735
|
| [2] |
Zanette L, White A, Allen M, et al. Perceived predation risk reduces the number of offspring songbirds produce per year. Science, 2011, 334(6061): 1398-1401
doi: 10.1126/science.1210908
pmid: 22158817
|
| [3] |
Suraci J, Clinchy M, Dill L, et al. Fear of large carnivores causes a trophic cascade. Nat Commun, 2016, 7(1): Article 10698
|
| [4] |
Hua F, Sieving K, Fletcher R, et al. Increased perception of predation risk to adults and offspring alters avian reproductive strategy and performance. Behav Ecol, 2014, 25(3): 509-519
|
| [5] |
Wirsing A, Ripple W. A comparison of shark and wolf research reveals similar behavioral responses by prey. Front Ecol Environ, 2011, 9: 335-341
|
| [6] |
Bauman A G, Seah J C L, Januchowski-Hartley F A, et al. Fear effects associated with predator presence and habitat structure interact to alter herbivory on coral reefs. Biol Lett, 2019, 15(10): 20190409
|
| [7] |
Wang X, Zanette L, Zou X. Modelling the fear effect in predator-prey interactions. J Math Biol, 2016, 73(5): 1179-1204
pmid: 27002514
|
| [8] |
Sasmal S. Population dynamics with multiple Allee effects induced by fear factors-A mathematical study on prey-predator interactions. Appl Math Model, 2018, 64: 1-14
|
| [9] |
Panday P, Samanta S, Pal N, et al. Delay induced multiple stability switch and chaos in a predator-prey model with fear effect. Math Comput Simul, 2020, 172: 134-158
|
| [10] |
Wang J, Cai Y, Fu S, et al. The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2019, 29: 083109
|
| [11] |
Antwi-Fordjour K, Parshad R D, Thompson H E, et al. Fear-driven extinction and (de) stabilization in a predator-prey model incorporating prey herd behavior and mutual interference. AIMS Math, 2023, 8(2): 3353-3377
|
| [12] |
Dai B, Sun G. Turing-Hopf bifurcation of a delayed diffusive predator-prey system with chemotaxis and fear effect. Appl Math Lett, 2021, 111: 106644
|
| [13] |
Zhang X, An Q, Wang L. Spatiotemporal dynamics of a delayed diffusive ratio-dependent predator-prey model with fear effect. Nonlinear Dyn, 2021, 105: 3775-3790
|
| [14] |
Tiwari V, Tripathi J, Mishra S, et al. Modeling the fear effect and stability of non-equilibrium patterns in mutually interfering predator-prey systems. Appl Math Comput, 2020, 371: 124948
|
| [15] |
Major P. Predator-prey interactions in two schooling fishes, caranx ignobilis and stolephorus purpureus. Anim Behav, 1978, 26: 760-777
|
| [16] |
Scheel D, Packer C. Group hunting behaviour of lions: a search for cooperation. Anim Behav, 1991, 41(4): 697-709
|
| [17] |
Ajraldi V, Pittavino M, Venturino E. Modeling herd behavior in population systems. Nonlinear Anal Real World Appl, 2011, 12(4): 2319-2338
|
| [18] |
Xu C, Yuan S, Zhang T. Global dynamics of a predator-prey model with defense mechanism for prey. Appl Math Lett, 2016, 62: 42-48
|
| [19] |
Manna D, Maiti A, Samanta G. Analysis of a predator-prey model for exploited fish populations with schooling behavior. Appl Math Comput, 2018, 317: 35-48
|
| [20] |
Melchionda D, Pastacaldi E, Perri C, et al. Social behavior-induced multistability in minimal competitive ecosystems. Theor Biol, 2017, 439: 24-38
|
| [21] |
Jiang H. Turing bifurcation in a diffusive predator-prey model with schooling behavior. Appl Math Lett, 2019, 96: 230-235
|
| [22] |
Yang J, Zhang T, Yuan S. Turing pattern induced by cross-diffusion in a predator-prey model with pack predation-herd behavior. Int J Bifurcation Chaos, 2020, 30(7): 2050103
|
| [23] |
Zhou Y, Yan X, Zhang C. Turing patterns induced by self-diffusion in a predator-prey model with schooling behavior in predator and prey. Nonlinear Dyn, 2021, 105: 3731-3747
|
| [24] |
Lou Y, Ni W. Diffusion, self-diffusion and cross-diffusion. J Differ Equations, 1996, 131(1): 79-131
|
| [25] |
Lou Y, Ni W, Yotsutani S. Pattern formation in a cross-diffusion system. Discrete Contin Dyn A, 2015, 35(4): 1589-1607
|
| [26] |
Wang S, Zhang J, Xu F, et al. Dynamics of virus infection models with density-dependent diffusion. Comput Math Appl, 2017, 74(10): 2403-2422
|
| [27] |
Zhou X, Shi X, Song X. Analysis of nonautonomous predator-prey model with nonlinear diffusion and time delay. Appl Math Comput, 2008, 196(1): 129-136
|
| [28] |
Zhang X, Chen L. The linear and nonlinear diffusion of the competitive Lotka-Volterra model. Nonlinear Anal, 2007, 66(12): 2767-2776
|
| [29] |
Wang J, Wei J, Shi J. Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems. J Differ Equations, 2016, 260(4): 3495-3523
|
| [30] |
Tang X, Song Y. Bifurcation analysis and Turing instability in a diffusive predator-prey model with herd behavior and hyperbolic mortality. Chaos Solitons Fractals, 2015, 81(A): 303-314
|
| [31] |
Yi F, Wei J, Shi J. Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system. J Differ Equations, 2009, 246(5): 1944-1977
|
| [32] |
Shi J, Wang C, Wang H, et al. Diffusive spatial movement with memory. J Dyn Differ Equations, 2020, 32: 979-1002
|
| [33] |
Song Y, Peng Y, Zhang T. The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system. J Differ Equations, 2021, 300: 597-624
|
| [34] |
Shi J, Wang C, Wang H. Spatial movement with diffusion and memory-based self-diffusion and cross-diffusion. J Differ Equations, 2021, 305: 242-269
|
| [35] |
Jiang W, Wang H, Cao X. Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay. J Dyn Differ Equations, 2019, 31: 2223-2247
|
| [36] |
Chen S, Lou Y, Wei J. Hopf bifurcation in a delayed reaction-diffusion-advection population model. J Differ Equations, 2018, 264(8): 5333-5359
|
| [37] |
Wu D, Zhao H. Spatiotemporal dynamics of a diffusive predator-prey system with Allee effect and threshold hunting. J Nonlinear Sci, 2020, 30: 1015-1054
|
| [38] |
Zhou P, Xiao D. Global dynamics of a classical Lotka-Volterra competition-diffusion-advection system. J Funct Anal, 2018, 275(2): 356-380
|
| [39] |
Chen M, Wu R. Spatiotemporal patterns induced by Turing and Turing-Hopf bifurcations in a predator-prey system. Appl Math Comput, 2020, 380: 1-15
|
| [40] |
Luo D, Wang Q. Global bifurcation and pattern formation for a reaction-diffusion predator-prey model with prey-taxis and double Beddington-DeAngelis functional responses. Nonlinear Anal Real World Appl, 2022, 67: 103638
|
| [41] |
Song Y, Zhang T, Peng Y. Turing-Hopf bifurcation in the reaction-diffusion equations and its applications. Commun Nonlinear Sci Numer Simul, 2016, 33: 229-258
|
 ),Song Yongli2(
),Song Yongli2( ),Xia Yonghui3,*(
),Xia Yonghui3,*( )
)