数学物理学报 ›› 2024, Vol. 44 ›› Issue (6): 1577-1594.
一个扩散模型中恐惧效应与集群行为协同诱导的时空动力学研究
肖江龙1(
),宋永利2(),夏永辉3,*()
- 1浙江师范大学数学科学学院 浙江金华 321004
2杭州师范大学数学学院 杭州 311121
3佛山大学数学学院 广东佛山 528000
-
收稿日期:2023-08-02修回日期:2024-04-16出版日期:2024-12-26发布日期:2024-11-22 -
通讯作者:*夏永辉,Email: yhxia@zjnu.cn -
作者简介:肖江龙,Email:jianglongxiao@zjnu.edu.cn ;|宋永利,Email:songyl@hznu.edu.cn -
基金资助:国家自然科学基金(11931016);浙江省自然科学基金(LZ23A010001);浙江省自然科学基金(LZ24A010006)
Spatiotemporal Dynamics Induced by the Interaction Between Fear and Schooling Behavior in a Diffusive Model
Xiao Jianglong1(),Song Yongli2(),Xia Yonghui3,*()
- 1School of Mathematical Sciences, Zhejiang Normal University, Zhejiang Jinhua 321004
2School of Mathematics, Hangzhou Normal University, Hangzhou 311121
3School of Mathematics, Foshan University, Guangdong Foshan 528000
-
Received:2023-08-02Revised:2024-04-16Online:2024-12-26Published:2024-11-22 -
Supported by:NSFC(11931016);Natural Science Foundation of Zhejiang Province(LZ23A010001);Natural Science Foundation of Zhejiang Province(LZ24A010006)
摘要：
该文研究了在齐次 Neumann 边界条件下扩散的捕食者--猎物模型的时空动力学. 该文研究表明, 恐惧和集群行为之间的相互作用产生了非常丰富和有趣的时空动力学. 详细讨论了 Turing 不稳定性和 Turing-Hopf 分支产生的条件. 利用规范型理论对 Turing-Hopf 分支点附近的时空动力学进行了分类, 并用丰富的数值模拟验证了理论分析. 最后, 总结了恐惧效应对集群行为的巨大影响. 发现猎物的集群行为不能抵消高水平的恐惧, 但可以抵消低水平的恐惧. 此外, 恐惧效应与集群行为共同诱发了系统的 Turing 不稳定性. 然而, 对于没有集群行为的系统, 恐惧效应既不会改变共存平衡点的稳定性, 也不会引起系统产生周期解或 Turing 不稳定性.
中图分类号:
- 0175.23
引用本文
肖江龙, 宋永利, 夏永辉. 一个扩散模型中恐惧效应与集群行为协同诱导的时空动力学研究[J]. 数学物理学报, 2024, 44(6): 1577-1594.
Xiao Jianglong, Song Yongli, Xia Yonghui. Spatiotemporal Dynamics Induced by the Interaction Between Fear and Schooling Behavior in a Diffusive Model[J]. Acta mathematica scientia,Series A, 2024, 44(6): 1577-1594.
图9
(A) 恐惧对猎物和捕食者密度的负面影响图. 这里取 $c=1.5 ＜ \sigma=20$. (B)-(C) 系统 (2.1) 在 $\sigma-\theta$ 平面上的分支图. 红线和绿线分别表示正平衡点存在的分界线和 Hopf 分支曲线."
图1
系统 （1.5） 在平面 $\sigma-d_{1}$ 上的稳定性区域和分支图. 取 $d_{2}=0.5,\theta=3,c=1.5$. $H_{0}$ 和虚线分别表示 Hopf 分支曲线和 $E_{*}$ 存在的分界线. $l_{s}(s=2,3,4)$ 是 Turing 分支曲线. $H_{0}$ 和 $l_{2}$ 相交于点 $P(\sigma^{*}, d^{*}_{1})=(3.0625, 0.05)$."
图2
系统 （5.2） 在 Turing-Hopf 分支点 $(3.0625,0.05)$ 处的分支图"
图3
当 $(\epsilon_{1},\epsilon_{2})=(0.015,0.5)$ 位于区域 $S_{1}$ 内时, $E_{*}(0.3194,0.3194)$ 稳定. 初值是 $(0.3194+0.2\cos 2x, 0.3194-0.24 \cos 2x)$."
图4
当 $(\epsilon_{1},\epsilon_{2})=(0.001,0.002)$ 位于区域 $S_{2}$ 内时, $E_{*}(0.2503,0.2503)$ 不稳定且形如 $\cos 2x$ 个稳定的非常数稳态出现. 图(A)-(B) 的初值取 $(0.2503+0.1\cos 2x, 0.2503+0.01 \cos 2x)$, 图(C)-(D) 的初值取 $(0.2503-0.1\cos 2x, 0.2503-0.01 \cos 2x)$."
图5
当 $(\epsilon_{1},\epsilon_{2})=(0.0002,-0.0001)$ 位于区域 $S_{3}$ 内时, $E_{*}(0.25,0.25)$ 不稳定. 一个异宿轨将不稳定的空间齐次周期解与稳定的空间非齐次稳态连接起来. 初始值为 $(0.25+0.00001 \cos 2x, 0.25+0.00001 \cos 2x)$."
图6
当 $(\epsilon_{1},\epsilon_{2})=(-0.02,-0.3)$ 位于区域 $S_{4}$ 内时, $E_{*}(0.2063,0.2063)$ 不稳定且稳定的非常数稳态出现. 初值取 $(0.2063-0.006 \cos 2x, 0.2063+0.001 \cos 2x)$."
图7
当 $(\epsilon_{1},\epsilon_{2})=(-0.001,-0.0032)$ 位于区域 $S_{5}$ 内时, $E_{*}(0.2454,0.2454)$ 不稳定且稳定的周期解出现. 初值取 $(0.2454-0.008 \cos 2x, 0.28-0.008 \cos 2x)$."
图8
当 $(\epsilon_{1},\epsilon_{2})=(-0.005,-0.013)$ 位于区域 $S_{6}$ 内时, $E_{*}(0.2486,0.2486)$ 不稳定且稳定的空间齐次周期解出现. 初值取 $(0.249, 0.249+0.00001\cos 2x)$."
图10
(A) 取 $\sigma=3.5625,\theta=1000,c=0.1$. (B)--(C) 取 $d_{1}=0.065,d_{2}=0.5$ 且初值为 $(0.1+0.1\cos 2x,0.1+0.1 \cos 2x)$. 高水平的恐惧使猎物和捕食者都死亡."
图11
(A) 取 $\sigma=100,\theta=0.01,c=1.5$. (B)--(C) 取 $d_{1}=0.065,d_{2}=0.5$ 且初值为 $(30+30\cos 2x,30+30\cos 2x)$. 低水平的恐惧能使捕食者和猎物稳定到一定数量."
图12
(A) 取 $\sigma=3.0622,\theta=3,c=1.5$. (B)--(C) 取 $d_{1}=0.065,d_{2}=0.5$ 且初值为 $(0.26+0.001\cos 2x,0.26+0.001 \cos 2x)$. 恐惧效应引起系统产生周期解."
图13
恐惧效应对捕食者密度的负面影响图. 这里取 $c=1.5 ＜ \sigma=20$. 恐惧效应不影响猎物密度."
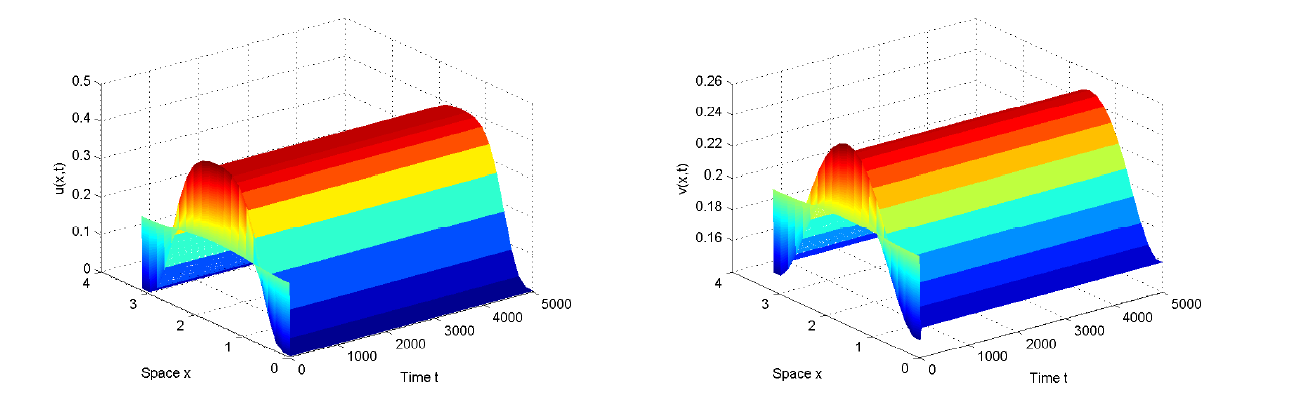
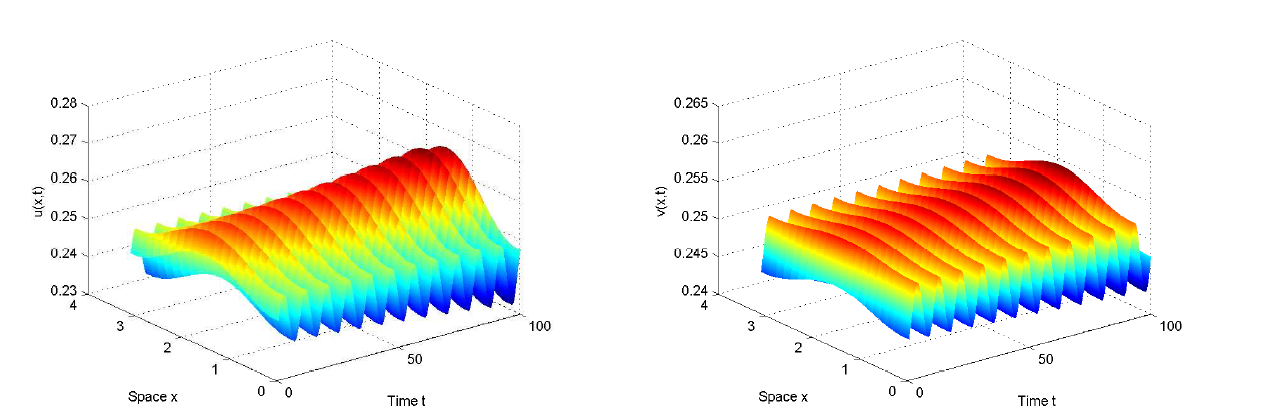
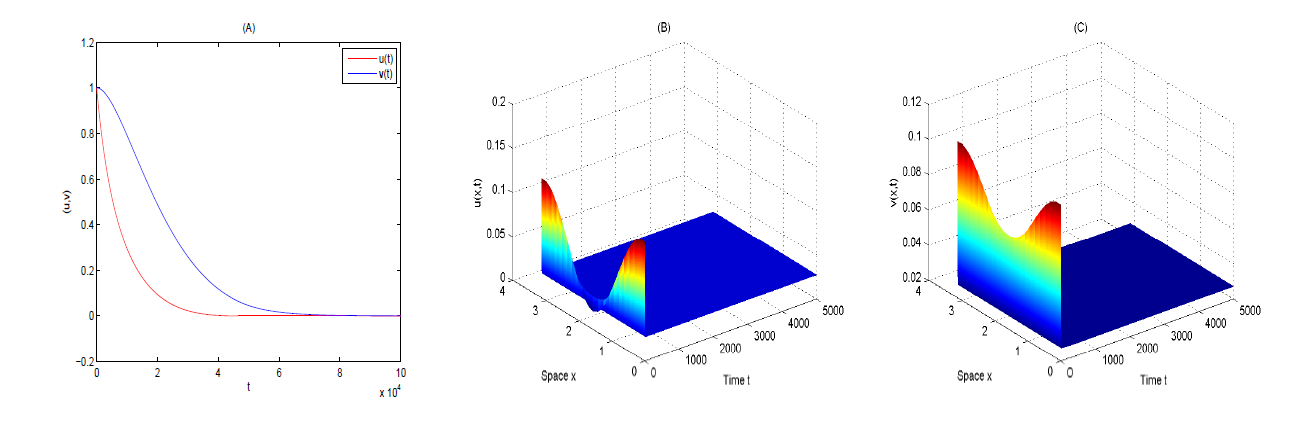
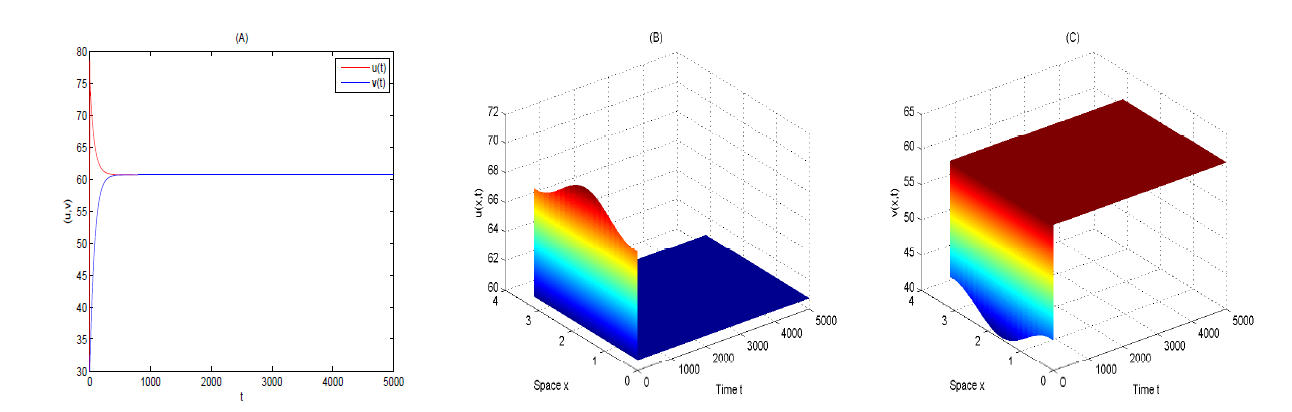
| [1] | Yang J, Yuan S, Zhang T. Complex dynamics of a predator-prey system with herd and schooling behavior: with or without delay and diffusion. Nonlinear Dyn, 2021, 104: 1709-1735 |
| [2] |
Zanette L, White A, Allen M, et al. Perceived predation risk reduces the number of offspring songbirds produce per year. Science, 2011, 334(6061): 1398-1401
doi: 10.1126/science.1210908 pmid: 22158817 |
| [3] | Suraci J, Clinchy M, Dill L, et al. Fear of large carnivores causes a trophic cascade. Nat Commun, 2016, 7(1): Article 10698 |
| [4] | Hua F, Sieving K, Fletcher R, et al. Increased perception of predation risk to adults and offspring alters avian reproductive strategy and performance. Behav Ecol, 2014, 25(3): 509-519 |
| [5] | Wirsing A, Ripple W. A comparison of shark and wolf research reveals similar behavioral responses by prey. Front Ecol Environ, 2011, 9: 335-341 |
| [6] | Bauman A G, Seah J C L, Januchowski-Hartley F A, et al. Fear effects associated with predator presence and habitat structure interact to alter herbivory on coral reefs. Biol Lett, 2019, 15(10): 20190409 |
| [7] |
Wang X, Zanette L, Zou X. Modelling the fear effect in predator-prey interactions. J Math Biol, 2016, 73(5): 1179-1204
pmid: 27002514 |
| [8] | Sasmal S. Population dynamics with multiple Allee effects induced by fear factors-A mathematical study on prey-predator interactions. Appl Math Model, 2018, 64: 1-14 |
| [9] | Panday P, Samanta S, Pal N, et al. Delay induced multiple stability switch and chaos in a predator-prey model with fear effect. Math Comput Simul, 2020, 172: 134-158 |
| [10] | Wang J, Cai Y, Fu S, et al. The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2019, 29: 083109 |
| [11] | Antwi-Fordjour K, Parshad R D, Thompson H E, et al. Fear-driven extinction and (de) stabilization in a predator-prey model incorporating prey herd behavior and mutual interference. AIMS Math, 2023, 8(2): 3353-3377 |
| [12] | Dai B, Sun G. Turing-Hopf bifurcation of a delayed diffusive predator-prey system with chemotaxis and fear effect. Appl Math Lett, 2021, 111: 106644 |
| [13] | Zhang X, An Q, Wang L. Spatiotemporal dynamics of a delayed diffusive ratio-dependent predator-prey model with fear effect. Nonlinear Dyn, 2021, 105: 3775-3790 |
| [14] | Tiwari V, Tripathi J, Mishra S, et al. Modeling the fear effect and stability of non-equilibrium patterns in mutually interfering predator-prey systems. Appl Math Comput, 2020, 371: 124948 |
| [15] | Major P. Predator-prey interactions in two schooling fishes, caranx ignobilis and stolephorus purpureus. Anim Behav, 1978, 26: 760-777 |
| [16] | Scheel D, Packer C. Group hunting behaviour of lions: a search for cooperation. Anim Behav, 1991, 41(4): 697-709 |
| [17] | Ajraldi V, Pittavino M, Venturino E. Modeling herd behavior in population systems. Nonlinear Anal Real World Appl, 2011, 12(4): 2319-2338 |
| [18] | Xu C, Yuan S, Zhang T. Global dynamics of a predator-prey model with defense mechanism for prey. Appl Math Lett, 2016, 62: 42-48 |
| [19] | Manna D, Maiti A, Samanta G. Analysis of a predator-prey model for exploited fish populations with schooling behavior. Appl Math Comput, 2018, 317: 35-48 |
| [20] | Melchionda D, Pastacaldi E, Perri C, et al. Social behavior-induced multistability in minimal competitive ecosystems. Theor Biol, 2017, 439: 24-38 |
| [21] | Jiang H. Turing bifurcation in a diffusive predator-prey model with schooling behavior. Appl Math Lett, 2019, 96: 230-235 |
| [22] | Yang J, Zhang T, Yuan S. Turing pattern induced by cross-diffusion in a predator-prey model with pack predation-herd behavior. Int J Bifurcation Chaos, 2020, 30(7): 2050103 |
| [23] | Zhou Y, Yan X, Zhang C. Turing patterns induced by self-diffusion in a predator-prey model with schooling behavior in predator and prey. Nonlinear Dyn, 2021, 105: 3731-3747 |
| [24] | Lou Y, Ni W. Diffusion, self-diffusion and cross-diffusion. J Differ Equations, 1996, 131(1): 79-131 |
| [25] | Lou Y, Ni W, Yotsutani S. Pattern formation in a cross-diffusion system. Discrete Contin Dyn A, 2015, 35(4): 1589-1607 |
| [26] | Wang S, Zhang J, Xu F, et al. Dynamics of virus infection models with density-dependent diffusion. Comput Math Appl, 2017, 74(10): 2403-2422 |
| [27] | Zhou X, Shi X, Song X. Analysis of nonautonomous predator-prey model with nonlinear diffusion and time delay. Appl Math Comput, 2008, 196(1): 129-136 |
| [28] | Zhang X, Chen L. The linear and nonlinear diffusion of the competitive Lotka-Volterra model. Nonlinear Anal, 2007, 66(12): 2767-2776 |
| [29] | Wang J, Wei J, Shi J. Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems. J Differ Equations, 2016, 260(4): 3495-3523 |
| [30] | Tang X, Song Y. Bifurcation analysis and Turing instability in a diffusive predator-prey model with herd behavior and hyperbolic mortality. Chaos Solitons Fractals, 2015, 81(A): 303-314 |
| [31] | Yi F, Wei J, Shi J. Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system. J Differ Equations, 2009, 246(5): 1944-1977 |
| [32] | Shi J, Wang C, Wang H, et al. Diffusive spatial movement with memory. J Dyn Differ Equations, 2020, 32: 979-1002 |
| [33] | Song Y, Peng Y, Zhang T. The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system. J Differ Equations, 2021, 300: 597-624 |
| [34] | Shi J, Wang C, Wang H. Spatial movement with diffusion and memory-based self-diffusion and cross-diffusion. J Differ Equations, 2021, 305: 242-269 |
| [35] | Jiang W, Wang H, Cao X. Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay. J Dyn Differ Equations, 2019, 31: 2223-2247 |
| [36] | Chen S, Lou Y, Wei J. Hopf bifurcation in a delayed reaction-diffusion-advection population model. J Differ Equations, 2018, 264(8): 5333-5359 |
| [37] | Wu D, Zhao H. Spatiotemporal dynamics of a diffusive predator-prey system with Allee effect and threshold hunting. J Nonlinear Sci, 2020, 30: 1015-1054 |
| [38] | Zhou P, Xiao D. Global dynamics of a classical Lotka-Volterra competition-diffusion-advection system. J Funct Anal, 2018, 275(2): 356-380 |
| [39] | Chen M, Wu R. Spatiotemporal patterns induced by Turing and Turing-Hopf bifurcations in a predator-prey system. Appl Math Comput, 2020, 380: 1-15 |
| [40] | Luo D, Wang Q. Global bifurcation and pattern formation for a reaction-diffusion predator-prey model with prey-taxis and double Beddington-DeAngelis functional responses. Nonlinear Anal Real World Appl, 2022, 67: 103638 |
| [41] | Song Y, Zhang T, Peng Y. Turing-Hopf bifurcation in the reaction-diffusion equations and its applications. Commun Nonlinear Sci Numer Simul, 2016, 33: 229-258 |
| [1] | 汪秋分, 张树文. 具有恐惧效应和 Holling III 功能性反应的随机捕食-食饵系统[J]. 数学物理学报, 2024, 44(5): 1380-1391. |
| [2] | 孙悦,张道祥,周文. 恐惧效应对带时滞的反应扩散捕食系统的稳定区间的影响[J]. 数学物理学报, 2021, 41(6): 1980-1992. |
|