1 引言
本文讨论如下弱非线性互补问题, 即寻求向量
其中
弱非线性互补问题在科学与工程领域有着广泛的应用. 例如, 运筹学, 均衡理论, 工程设计等. 当
它常出现于工程或经济等各类实际问题, 如双矩阵博弈的纳什均衡, 径向轴承的自由边值问题等[11, 19, 21]. 在文献[19] 中, Lemke通过研究双矩阵均衡点等问题引出线性互补问题. 关于该问题的算法构造与求解也一直是优化或数值代数领域的研究热点, 特别当矩阵
鉴于以上一些研究成果, 通过引入一个光滑函数及巧妙的等价变换, 我们提出了一个具有高阶收敛性的加速牛顿迭代法来求解一类大规模弱非线性互补问题, 其思想源于牛顿法至少具有二阶收敛性的优势. 数值实验部分将该算法与当前一些有效算法做了详细比较, 说明了所提出的算法是可行性且有效的.
为分析方便, 通篇文章给出如下一些记号: 设
本文剩余章节组织如下. 在第2节, 提出了一个求解弱非线性互补问题的带高阶收敛性的加速牛顿迭代法. 第3节详细分析了算法的收敛速率. 第4节给出了包括源于自由边值问题离散的弱非线性互补问题的一些数值结果, 充分验证了所构造的算法的有效性和可行性. 最后是结论部分.
2 高阶收敛性算法
这一节, 主要提出一个具有高阶收敛性的加速牛顿迭代法. 首先, 给出几个重要的引理和结论, 将弱非线性互补问题进行合理巧妙地转化, 从而能有助于利用所构造的算法进行有效求解, 并为下一节的收敛性分析做一些必要准备.
引理2.1 问题
其中
证 首先假设
令
由
这意味着
另一方面, 假设
其中
类似可得
从而
即为非线性方程组
接下来, 引入一个光滑函数
其中
如此一来, 可定义如下非线性可微函数
引理2.2 问题
其中
证 结论容易由公式(2.4) 及引理
引理2.3 非线性函数
其中,
证 式(2.6) 两边对变量
由(2.4) 式以及(2.5) 式可得
由于
下面, 给出求解非线性光滑函数
算法2.1 (高阶牛顿迭代法(HONM))
步1 给定初值点
步2 计算
步3 令
步4 计算
再计算
步5 令
步6 当
事实上, 高阶牛顿法(HONM) 亦可写成下列具体迭代格式
注2.1 根据引理
注2.2 参数
注2.3 若取
3 收敛性分析
本节我们着重讨论高阶牛顿迭代法(HONM) 的收敛性能. 首先给出一个定义及一些重要引理.
定义3.1[17] 令
鉴于经典的牛顿迭代法具有二阶收敛速度, 我们有下面的结论, 具体可参看文献[17] 以及其中涉及到的相关参考文献.
引理3.1[17] 假设
成立, 则牛顿迭代法至少二阶收敛, 其中常数
引理3.2[17] 假设
则对任意初始点
引理3.3[17] 假设
则
成立, 其中常数
下面将给出高阶加速牛顿迭代法的收敛性, 详细有如下定理.
定理3.1 假设
成立, 则
其中
证 首先, 考虑当
根据引理
其中
因此
其中最后一个等式源于
另外, 也注意到
令
若在不等式
这意味着对于
下面将用归纳法来证明迭代格式
由
假设
成立. 接下来证明
其中
由
其中
4 数值实验
或超过最大迭代次数
由算法1可知HONM是一般牛顿法的加速版本且具有高阶收敛速率. 但同时, 也注意到当
例4.1[23] 考虑问题(1.2), 即弱非线性互补问题的特殊形式, 其中
例4.2 该例问题来源于自由边值问题离散. 令
其中
在例
表 1 例4.1的数值结果
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 方法 | HONM | FBSN | HONM | FBSN | |
| n=500 | It | 2 | 11 | 3 | 11 |
| CPU | 0.1032 | 0.3788 | 0.1511 | 0.4340 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=1000 | It | 2 | 11 | 3 | 11 |
| CPU | 0.5880 | 1.1551 | 0.8808 | 1.3629 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=2000 | It | 2 | 11 | 3 | 11 |
| CPU | 3.2900 | 4.2802 | 5.1104 | 5.2537 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=2500 | It | 2 | 11 | 3 | 11 |
| CPU | 5.9151 | 6.4952 | 6.0723 | 8.0709 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 |
表 2 例4.1的数值结果
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | HONM | CBSN | HONM | CBSN | |
| n=800 | It | 2 | 3 | 3 | 4 |
| CPU | 0.3332 | 0.4838 | 0.4840 | 0.6879 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=1500 | It | 2 | 3 | 3 | 4 |
| CPU | 1.5395 | 2.3335 | 2.3196 | 3.0597 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=3000 | It | 2 | 3 | 3 | 4 |
| CPU | 10.4229 | 15.6110 | 15.6472 | 20.6621 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=5000 | It | 2 | 3 | 3 | 4 |
| CPU | 45.8406 | 65.4892 | 69.7337 | 89.2019 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 |
表 3 例4.2的数值结果, f(x, y, t) = t2
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.7936 | 29.2284 | 254.8708 | 1458.9 | |
| RES | 8.2364e-002 | 8.3124e-002 | 8.342e-002 | 8.333e-002 | |
| MMSA | It | 104 | 393 | 853 | 401 |
| CPU | 0.0326 | 2.3810 | 26.8192 | 40.3858 | |
| RES | 8.7282e-013 | 9.9680e-013 | 9.7832e-013 | 9.8603e-013 | |
| HONM | It | 9 | 9 | 2 | 2 |
| CPU | 0.0617 | 2.1585 | 3.3131 | 16.6964 | |
| RES | 0 | 0 | 0 | 0 |
表 4 例4.2的数值结果, f(x, y, t) = t + sin t
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.8202 | 31.4063 | 305.5803 | 1539.5 | |
| RES | 9.1410e-002 | 9.2369e-002 | 9.231e-002 | 9.261e-002 | |
| MMSA | It | 105 | 396 | 314 | 404 |
| CPU | 0.0317 | 2.3881 | 8.3169 | 36.5056 | |
| RES | 8.0910e-013 | 9.4929e-013 | 9.2611e-013 | 9.8210e-013 | |
| HONM | It | 7 | 7 | 2 | 2 |
| CPU | 0.0498 | 1.5487 | 2.1063 | 11.0249 | |
| RES | 1.1757e-015 | 1.0710e-016 | 0 | 0 |
表 5
例4.2的数值结果,
| 初始点 | z(3)0 | z(3)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.8505 | 31.2633 | 263.0305 | 1266.1 | |
| RES | 9.1410e-002 | 9.2369e-002 | 4.1121e-002 | 4.2001e-002 | |
| MMSA | It | 105 | 227 | 299 | 388 |
| CPU | 0.0244 | 1.4172 | 9.3599 | 37.8653 | |
| RES | 8.0910e-013 | 9.9726e-013 | 9.0592e-013 | 9.7484e-013 | |
| HONM | It | 2 | 2 | 2 | 2 |
| CPU | 0.0157 | 0.3998 | 2.2060 | 10.6302 | |
| RES | 0 | 0 | 0 | 0 |
表 6 例4.2的数值结果, f(x, y, t) = ln(1 + t)
| 初始点 | z(3)0 | z(3)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 8 | 9 | 10 | 10 |
| CPU | 0.0534 | 1.4129 | 13.8041 | 81.8000 | |
| RES | 1.3059e-008 | 1.5371e-007 | 7.4532e-008 | 4.8048e-007 | |
| MMSA | It | 114 | 222 | 297 | 388 |
| CPU | 0.0273 | 1.3339 | 9.3883 | 41.4062 | |
| RES | 8.9631e-013 | 9.6913e-013 | 9.9131e-013 | 9.2350e-013 | |
| HONM | It | 2 | 2 | 2 | 2 |
| CPU | 0.0156 | 0.3238 | 2.1165 | 12.1649 | |
| RES | 0 | 0 | 0 | 0 |
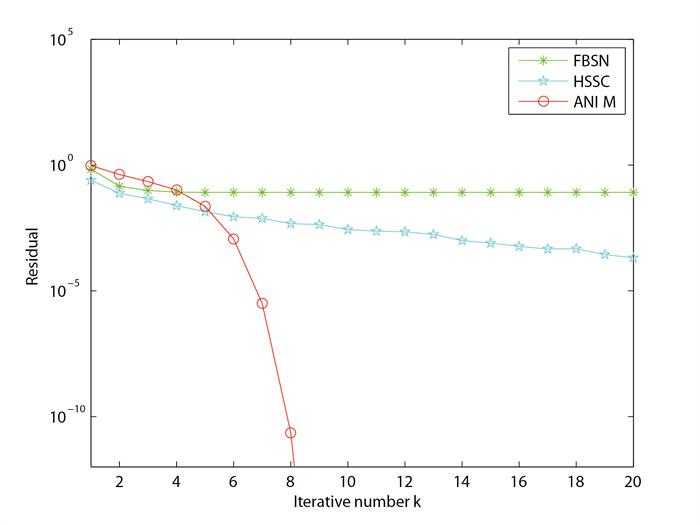
图 1
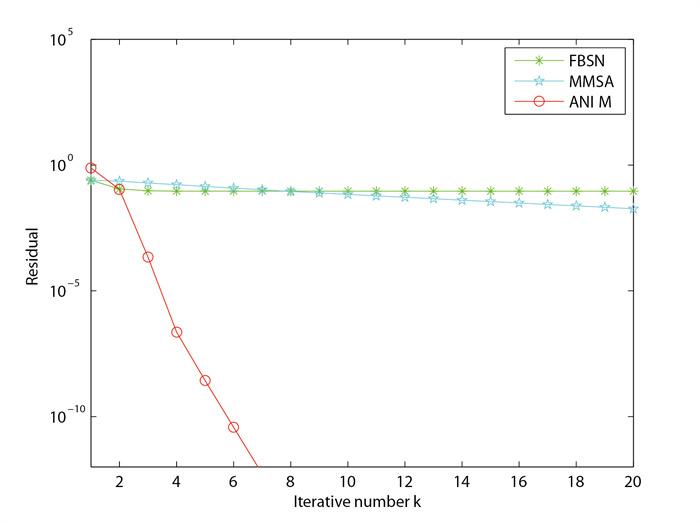
图 2
5 结论
参考文献
Modulus-based matrix splitting iteration methods for linear complementarity problems
On the convergence of the multisplitting methods for the linear complementarity problem
Experimental study of the asynchronous multisplitting relaxtation methods for linear complementarity problems
Matrix multisplitting relaxtion methods for linear complementarity problem
DOI:10.1080/00207169708804569 [本文引用: 1]
Matrix multisplitting methods with applications to linear complementarity problems: Parallel synchronous and chaotic methods
Parallel chaotic multisplitting iterative methods for the large spase linear complementarity problem
Matrix multisplitting methods with applications to linear complementarity problems: Parallel asynchronous methods
DOI:10.1080/00207160211927 [本文引用: 1]
A class of asynchronous iterations for the linear complementarity problem
Modulus-based synchronous multisplitting iteration methods for linear complementarity problems
DOI:10.1002/nla.1835 [本文引用: 1]
Smoothing methods and semismooth methods for nondifferentiable operator equations
DOI:10.1137/S0036142999356719 [本文引用: 1]
The solution of a quadratic programming using systematic overrelaxation
A special Newton-type optimization method
DOI:10.1080/02331939208843795 [本文引用: 1]
Using vector divisions in solving the linear complementarity problem
Krylov subspace methods to solve a class of tensor equations via the Einstein product
The modulus-based matrix splitting algorithms for a class of weakly nonlinear complementarity problems
DOI:10.1002/nla.2039 [本文引用: 2]
A new nonsmooth equations approach to nonlinear complementarity problems
DOI:10.1137/S0363012994276494 [本文引用: 1]
Bimatrix equilibrium points and mathematical programming
DOI:10.1287/mnsc.11.7.681 [本文引用: 2]
A semismooth equation approach to the solution of nonlinear complementarity problems
A nonsmooth version of Newtons method
DOI:10.1007/BF01581275 [本文引用: 1]
A monotone semismooth Newton type method for a class of complementarity problems
DOI:10.1016/j.cam.2010.08.012 [本文引用: 2]
On linear convergence of iterative method for the variational inequality problem
DOI:10.1016/0377-0427(94)00094-H [本文引用: 1]
Neural network approaches based on new NCP-functions for solving tensor complementarity problem
A cosh-based smoothing Newton method for P0 nonlinear complementarity problem
Two-step modulus based matrix splitting iteration for linear complementarity problems
Accelerated modulus-based matrix splitting iteration methods for linear complementarity problem