1 引言
给定复矩阵
TSVD经常被用在病态问题[1, 2]的解决上. 在病态模型问题中, 模型的病态性主要体现在系数矩阵的小奇异值对参数及其方差的放大. 截断奇异值法的基本思想是将这些小的奇异值截掉并重构系数阵以削弱模型的病态性. 如在生物发光断层成像(BLT)[3]中, 由于BLT重建问题中系数矩阵
其中
其中
其中
以及任意
对正整数
和同构映射
则复Stiefel流形
进而问题(1.2)可转化为如下实数域上乘积流形约束黎曼优化问题
其中
其中
针对以上分析, 本文在文献[7–9]的基础上进一步研究针对复数域上问题(1.2) 的基于目标函数二阶导数信息的黎曼牛顿求解算法. 对于黎曼牛顿法, 有效求解导出的牛顿方程和设计有效初值选取方案是关键. 针对牛顿方程, 本文基于乘积流形上切空间的等价形式, 写出黎曼海塞在切空间上的变换矩阵, 进而基于克罗内克积和复数域上的若干矩阵拉直算子, 将复数域上的黎曼牛顿方程转化为实数域上标准对称线性方程组, 进而利用相关的Krylov子空间方法求解; 针对初值选取, 本文利用黎曼优化中具有单步迭代成本低且存储量少等优点的经典一阶梯度算法OptStiefelGBB[12]来选取迭代初值, 进而得到一类黎曼混合牛顿法. 充分的数值实验和数值比较说明, 本文针对问题(1.2) 设计的基于黎曼牛顿法的混合算法是切实可行的, 其中数值比较包括黎曼优化工具箱Manopt[19]中的原始信赖域算法和黎曼BFGS算法, 以及适用于问题(1.2) 的具有不同形式的若干黎曼梯度类算法.
本文余下内容组织如下: 第二节给出复乘积流形
2 预备知识
黎曼优化是指黎曼流形
下面简要给出复乘积流形
复乘积流形
因复乘积流形
其中
其中
分别表示
下面讨论问题(1.2)中目标函数
引理2.1 目标函数
证 因为复乘积流形
其中
进而由(2.4)式和(2.5)式可得
引理2.1得证.
引理2.2 令
证
利用
注意到
在(2.14)式的最后一个等式中用到了
记
利用(2.16)式的结论可以简化(2.14)式最后一个等式中
根据(2.14)式的最后一个等式,
将(2.8)式和(2.17)代入上式即得(2.11). 引理2.2得证.
本节最后给出下文需用到的若干矩阵拉直算子的定义及相关性质.
易知
1.
2.
其中
3.
记
定义2.1
由定义易得如下等式
引理2.3[17]
矩阵
为建立复数和实向量, 复矩阵和实矩阵对之间联系, 定义同构映射
下面给出拉直算子
1.
2. 记
3.
其中
4.
其中
3 基于黎曼牛顿法的混合算法求解问题(1.2)
对于迭代框架(2.1), 通过求解如下黎曼牛顿方程得到黎曼牛顿法在当前迭代步
若已求得
其中牛顿法的迭代步长通常设置为1. 将(2.7), (2.11)式代入(3.1) 式, 得到黎曼牛顿方程的具体形式为(为方便讨论省略上标)
其中搜索方向
下面讨论如何求解牛顿方程(3.3). 注意到搜索方向
引理3.1[12] 复乘积流形
其中
由引理3.1可知
令
其中
下面引理给出了由
引理3.2
证 结合引理2.2中黎曼海塞的表达式(2.11)和(3.5), 可知
注意到
进一步由
由
进而由
记
引理3.3 令
其中
其中
其中
证 因为
注意到
由(3.7)式, 结合(2.25)–(2.29)式以及(3.16)式和(3.20)式,
类似于
引理3.3得证.
推论3.1 在黎曼度量(2.3)下, 矩阵
证
其中
因为黎曼海塞是对称变换[13], 即
结合引理3.3, 上式等价于
进而由
接下来求解牛顿方程(3.3). 由(3.5)式, 牛顿方程可以改写成
在(3.24)式两边分别左乘
再
最后由引理3.3, 牛顿方程(3.3)可转化为如下线性方程组形式
其中
因变换矩阵
基于以上讨论, 求解问题(1.2)的黎曼牛顿法的完整迭代格式如下:
算法1 求解问题(1.2)的黎曼牛顿法(Newton)
1. 给定初始点
2. 对
3. 计算
4. 由引理3.3和(3.28)分别计算
5. 将
6. 重构
7. 计算
8. 计算更新迭代步
9. 循环结束.
注3.1 算法Newton中第3步的
注3.2 对于算法Newton中的实对称线性方程组
注3.3 一般来说, 由(3.1)式得到的搜索方向
由上式可知, 若要使得
其中
故可采用变换矩阵
注3.4 类似于无约束优化,
其中
其中
一般来说牛顿法不能保证全局收敛, 且对迭代初值的选取比较敏感. 这里我们应用黎曼优化中的经典一阶梯度类算法OptStiefelGBB[12]来产生一个合适的迭代初值. 该一阶算法的优势在于单步迭代成本低且存储量少. 对于迭代框架(2.1), 算法OptStiefelGBB利用非单调Armijo原则来得到步长
为加速收敛, 初始步长
其中
其中
算法2 求解问题(1.2)的黎曼梯度类算法(OptStiefelGBB)
1. 任取初始值
2. 对
3. 计算搜索方向
4. 根据(3.31)式计算
5. 计算迭代更新步
6. 循环结束.
为加速收敛, 我们提出一类基于黎曼牛顿法的混合算法, 其迭代框架如下
算法3 求解问题(1.2)的黎曼牛顿混合算法(Hybrid-Newton)
1. 任取初始值
2. 对
3. 执行算法OptStiefelGBB中的第3–5步.
4.
5. 循环结束.
6. 令
7. 执行算法Newton的第2–9步.
算法OptStiefelGBB具有全局收敛性[12], Stiefel流形上黎曼牛顿法具有局部二阶收敛速度, 见文献[13, 定理6.3.2], 故算法Hybrid-Newton集合了两种算法的优点, 即有如下结论
定理3.1 任意给定初始值
4 数值实验
本节给出算法Hybrid-Newton求解问题(1.2)的数值结果. 所有的数据均通过MATALB (R2019), Intel
其中
在实际计算中, 算法Newton中实对称线性方程组(3.29)均采用CR方法求解, 其迭代终止标准取为
其中
其中
为数值比较, 本节将算法Hybrid-Newton与黎曼优化工具箱Manopt[19]中的黎曼信赖域方法(记为Existing RTR) 和黎曼BFGS方法(记为Existing RBFGS), 以及黎曼梯度类方法进行比较. 值得说明的是文献[20]将欧式空间中的Dai非线性共轭梯度法[21]推广到实Stiefel流形, 文献[22]将其推广到实乘积流形
其中
其中
这里
例4.1 本例说明算法Hybrid-Newton的全局收敛性和算法Newton中CR方法对于求解实对称线性组(3.29) 的有效性. 取定
其中
其中
为说明算法的全局收敛性, 算法Hybrid-Newton取不同的迭代初值
表 1 不同初值下算法Hybrid-Newton的数值结果
| CT.(s) | IT. | Grad. | Obj. | CT.(s) | IT. | Grad. | Obj. | ||
| Hybrid-Newton | 3.31 | 96/5 | 1.38 | -56.23 | 1.38 | 157/3 | 3.81 | -56.23 | |
| Hybrid-Newton | 3.14 | 159/5 | 1.74 | -56.22 | 3.66 | 187/7 | 6.03 | -56.23 | |
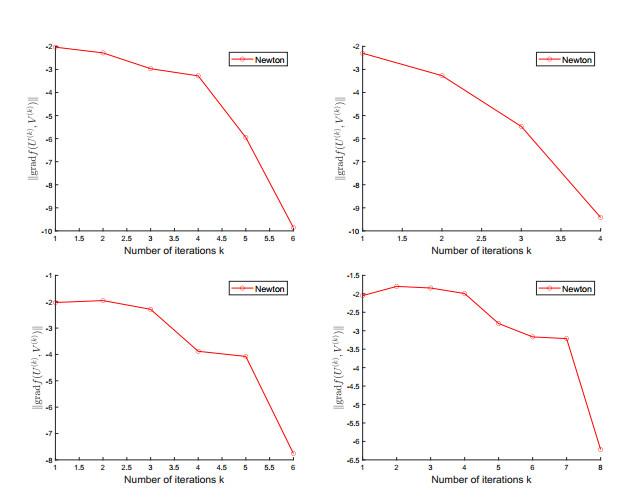
图 1
图 1
经算法OptStiefelGBB生成合适迭代初值后, 算法Newton中黎曼梯度范数
表 2 算法Newton中CR方法求解实对称线性方程组(3.29)的数值结果
| L | CT.(s) | IT. | L | CT.(s) | IT. | |||
| 1 | 0.75 | 130 | 1.78 | 1 | 0.49 | 123 | 2.45 | |
| 2 | 0.60 | 161 | 5.78 | 2 | 0.39 | 95 | 1.27 | |
| 3 | 0.53 | 140 | 3.82 | 3 | 0.29 | 72 | 5.67 | |
| 4 | 0.30 | 71 | 9.47 | |||||
| 5 | 0.33 | 86 | 3.49 | |||||
| 1 | 0.84 | 148 | 7.49 | 1 | 0.26 | 69 | 2.77 | |
| 2 | 0.75 | 142 | 5.82 | 2 | 0.50 | 129 | 5.91 | |
| 3 | 0.44 | 113 | 8.08 | 3 | 0.47 | 118 | 3.28 | |
| 4 | 0.49 | 132 | 4.50 | 4 | 0.63 | 147 | 9.80 | |
| 5 | 0.23 | 59 | 6.50 | 5 | 0.43 | 112 | 2.45 | |
| 6 | 0.59 | 149 | 1.24 | |||||
| 7 | 0.29 | 77 | 4.70 | |||||
例4.2 本例给出算法Hybrid-Newton与黎曼优化工具箱Manopt中的两类经典二阶算法, 即Exsiting-RTR和Exsiting-RBFGS, 以及黎曼梯度类算法OptStiefelGBB和RCG-Cayley的数值比较结果. 按下列方式生成问题(1.2) 中的矩阵
为数值比较, 各算法的迭代初值均取为
其中
表 3 不同算法的数值比较结果
| CT.(s) | IT. | Grad. | Obj. | CT.(s) | IT. | Grad. | Obj. | ||
| Hybrid-Newton | 0.32 | 80/3 | 1.92 | -116.67 | 1.21 | 134/3 | 1.29 | -156.31 | |
| Existing-RTR | 0.38 | 13 | 5.38 | -116.67 | 0.83 | 14 | 5.35 | -156.31 | |
| Existing-RBFGS | 3.93 | 145 | 9.87 | -116.67 | 5.14 | 194 | 8.56 | -156.31 | |
| OptStifelGBB | 0.06 | 199 | 8.87 | -116.67 | 0.16 | 284 | 2.14 | -156.31 | |
| RCG-Cayley | 0.10 | 182 | 8.63 | -116.67 | 0.28 | 293 | 9.15 | -156.31 | |
| Hybrid-Newton | 2.64 | 149/5 | 1.33 | -189.95 | 4.80 | 173/3 | 4.90 | -223.22 | |
| Existing-RTR | 0.99 | 15 | 2.62 | -189.95 | 1.37 | 15 | 5.17 | -223.22 | |
| Existing-RBFGS | 6.70 | 239 | 9.54 | -189.95 | 6.51 | 216 | 9.83 | -223.22 | |
| OptStifelGBB | 0.37 | 396 | 4.04 | -189.95 | 0.47 | 430 | 9.49 | -223.22 | |
| RCG-Cayley | 0.50 | 362 | 9.08 | -189.95 | 0.64 | 363 | 9.98 | -223.22 | |
| Hybrid-Newton | 5.26 | 148/2 | 2.80 | -245.29 | 10.95 | 210/ 4 | 2.46 | -272.71 | |
| Existing-RTR | 1.45 | 14 | 3.48 | -245.29 | 1.51 | 15 | 3.14 | -272.71 | |
| Existing-RBFGS | 9.60 | 304 | 2.45 | -245.29 | 9.49 | 285 | 1.30 | -272.71 | |
| OptStifelGBB | 0.61 | 408 | 3.60 | -245.29 | 0.75 | 423 | 8.00 | -272.71 | |
| RCG-Cayley | 0.84 | 406 | 7.70 | -245.29 | 1.15 | 471 | 8.49 | -272.71 | |
| Hybrid-Newton | 16.85 | 159/4 | 6.93 | -293.84 | 21.11 | 265/3 | 2.21 | -316.66 | |
| Existing-RTR | 2.26 | 15 | 2.24 | -293.84 | 3.11 | 15 | 4.91 | -316.66 | |
| Existing-RBFGS | 11.99 | 275 | 2.59 | -293.84 | 18.02 | 355 | 7.76 | -316.66 | |
| OptStifelGBB | 0.89 | 408 | 8.12 | -293.84 | 2.62 | 587 | 9.07 | -316.66 | |
| RCG-Cayley | 1.32 | 438 | 8.16 | -293.84 | 5.44 | 835 | 8.26 | -316.66 | |
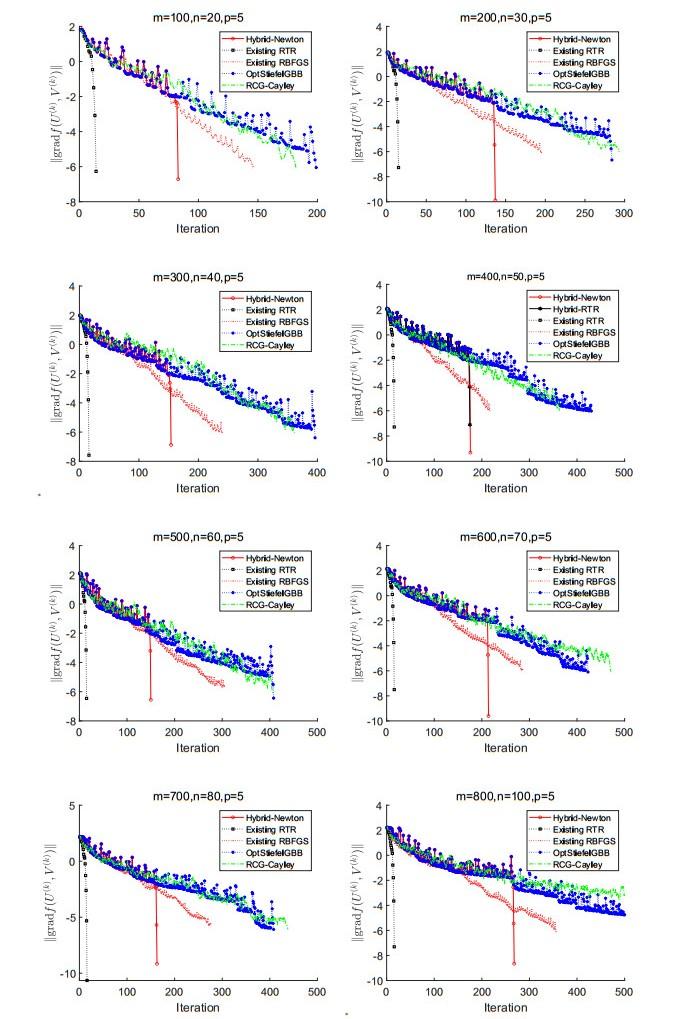
图 2
5 结论
本文应用黎曼优化中的黎曼牛顿法和黎曼信赖域算法求解复矩阵截断奇异值分解问题(1.2). 对于黎曼牛顿法, 关键问题是如何有效求解对应的黎曼牛顿方程. 本文利用若干矩阵拉直算子和克罗内克积, 将其转化为容易求解的实对称线性方程组, 达到降维和简化计算的目的. 因为牛顿法对迭代初值比较敏感, 本文利用具有全局收敛性, 且迭代成本低, 存储量少的黎曼一阶经典算法OptStiefelGBB产生初值. 进而设计的混合算法同时具有全局收敛和局部二次收敛特性. 数值实验和数值比较验证, 对于中小规模的复矩阵截断奇异值分解问题, 本文设计的算法是切实有效的.
在数值实验中我们发现, 对于大规模的复矩阵截断奇异值问题, 黎曼牛顿法中求解实对称线性方程组需要花费大量时间. 故寻求更有效地方式求解黎曼牛顿方程是下一阶段的研究工作. 另外, 以迭代法求解黎曼牛顿方程导出的实对称线性方程组实质上是非精确地方式处理黎曼牛顿方程, 故寻求更有效方式非精确求解黎曼牛顿方程, 并细致分析对应非精确黎曼牛顿法, 如Guass-Newton, CG-Newton等的收敛性是下一步工作重点. 另外, 在目标函数中加入正则化项, 进而采用正则化牛顿法或邻近牛顿法求解, 也是下一步的研究工作.
参考文献
Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank
A modified truncated singular value decomposition method for discrete ill-posed problems
DOI:10.1002/nla.1938 [本文引用: 1]
Truncated singular value decomposition for through-the-wall microwave imaging application
Application of low-rank approximation using truncated singular value decomposition for noise reduction in hyperpolarized 13C NMR spectroscopy
A Riemannian optimization approach to the matrix singular value decomposition
DOI:10.1137/120872887 [本文引用: 4]
A matrix-free implementation of Riemannian Newton's method on the Stiefel manifold
DOI:10.1007/s11590-016-1090-9 [本文引用: 1]
The analytic solutions of a class of constrained matrix minimization and maximization problems with applications
DOI:10.1137/17M1140777 [本文引用: 2]
A feasible method for optimization with orthogonality constraints
Optimization Algorithms on Matrix Manifolds
A brief introduction to manifold optimization
DOI:10.1007/s40305-020-00295-9 [本文引用: 1]
The vec-permutation matrix, the vec operator and Kronecker products: A review
DOI:10.1080/03081088108817379 [本文引用: 2]
Least squares Hermitian solution of the matrix equation (AXB, CXD)=(E, F) with the least norm over the skew field of quaternions
Manopt, a Matlab toolbox for optimization on manifolds
A Riemannian conjugate gradient method for optimization on the Stiefel manifold
DOI:10.1007/s10589-016-9883-4 [本文引用: 3]
A nonmonotone conjugate gradient algorithm for unconstrained optimization
A Riemannian optimization approach for solving the generalized eigenvalue problem for nonsquare matrix pencils