1 引言
考虑如下的EFK方程的初边值问题
其中
对于方程(1.1) 的数值方法的研究, 已有了一些结果. 例如, 在一维情形下, 文献[5]提出了一种二阶分裂与正交三次样条配置相结合的方法, 导出了半离散格式解在最大模意义下的界与最优误差估计. 文献[6]利用边界元方法对其进行了数值分析. 文献[7]导出了有限元解的半离散格式和Crank-Nicolson全离散格式下的最优误差估计. 在二维情形下, 文献[8]和文献[9]分别提出了Crank-Nicolson有限差分格式和一种二阶线性隐式有限差分格式, 证明了数值解的存在唯一性, 并得到了其在
由于具有对空间光滑度要求较低, 并能同时得到原始变量和空间变量的误差估计等优势, 方程(1.1) 的混合有限元方法也一直受到人们的关注. 例如, 文献[12]利用协调线性三角形
众所周知, Wilson元是工程计算中常用的数值效果很好的矩形非协调元, 关于它的高精度分析已有很多结果. 例如, 文献[16]证明了在能量模意义下Wilson元的相容误差为
本文的主要目的是对非线性方程(1.1) 的间断有限元的收敛性展开研究. 首先, 证明半离散格式逼近解的存在唯一性. 其次, 利用Wilson元在新范数意义下的插值估计和双线性型的性质导出半离散格式下原始变量
本文中,
其中
2 有限元的构造及性质
设
设
Wilson元的形函数空间为
其中
定义
引理2.1 设
引理2.2 设
其中
定义
其中
由
由文献[29]可知: 对任何
这里
3 半离散格式的收敛性分析
令
问题(3.1) 的变分问题为:求
问题(3.1) 的传统的半离散格式为:求
由文献[17]知其误差估计为
为提高收敛阶, 我们引进新的半离散格式为: 求
引理3.1 问题(3.4) 存在唯一解.
引理3.2 若
其中,
下面给出收敛性结果.
定理3.1 设
证 令
由(3.2)和(3.4)式, 可得下面的误差方程
一方面, 当
下面对
利用Sobolev嵌入定理
注意到
将上述关于
上式两边对变量
由文献[24]知: 存在
于是, 当
因此, 存在充分小的
于是, 假设错误, 即
另一方面, 在(3.7(a)) 式中取
类似于
下面对
利用Sobolev嵌入定理, 并注意到
于是
将(3.14) 式以及以上关于
上式两边关于变量
类似于(3.11) 式
利用
将(3.12) 式、(3.16) 式及上述关于
再利用Gronwall引理得
综上, 由引理2.1和三角不等式, 易知(3.6) 式成立. 证毕.
4 全离散逼近格式的收敛性分析
在本节中, 将对问题(3.1) 的向后Euler全离散格式的误差进行分析和估计.
将时间区间
取
其中,
建立(4.1) 式的全离散逼近格式如下: 求
类似于文献[15], 可以证明问题(4.2) 存在唯一解.
定理4.1 设
证 记
由(4.1) 和(4.2) 式得误差方程为
根据泰勒公式, 易得
由于
首先, 我们用数学归纳法证明存在
这里,
当
于是, 当
当
下面对
成立
利用(2.2) 式及(4.5) 式, 可得
注意到
及
成立, 则有
由于
而由Sobolve嵌入定理, (2.4) 式及(4.8) 式有
于是
将上述关于
成立, 再将
对上式应用离散的Gronwall引理, 存在正常数
取
其次, 我们证明存在
这里,
当
当
在(4.15(a)) 式中取
下面对
及
有
及
利用(4.5) 式, 并注意到
则有
再次利用(4.10) 式、(4.12) 式和(2.2) 式, 同时注意到引理2.1成立, 可得
而利用(4.11) 式有
及
类似于
而利用泰勒公式可得
将上面两式的估计代入(4.21) 式, 可得
利用
其中,
因此当
利用
再利用
可得
将(4.23) 式和(4.24) 式的估计代入(4.22) 式可得, 当
将
将
对上式应用离散的Gronwall引理, 存在正常数
取
综上, 再利用引理2.1和三角不等式, 易知(4.3) 式成立.
注4.2 在定理4.1的证明中, 对于非线性项
5 数值实验
在这一节, 我们将给出一个数值算例来验证理论分析的正确性和算法的有效性. 考虑如下EFK方程
其中
确定的函数. 令
我们将区域
表 1
| 收敛阶 | 收敛阶 | |||
| 0.000046035 | — | 0.005970921 | — | |
| 0.000012875 | 1.8381 | 0.001790764 | 1.7374 | |
| 0.000003264 | 1.9799 | 0.000472460 | 1.9223 | |
| 0.000000793 | 2.0417 | 0.000117908 | 2.0025 | |
| 0.000000195 | 2.0240 | 0.000029285 | 2.0094 |
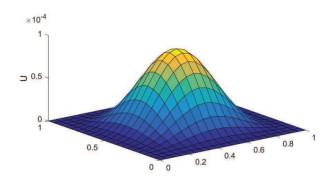
图 1
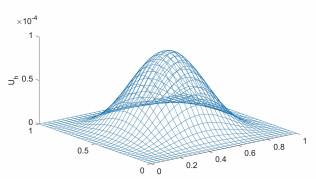
图 2
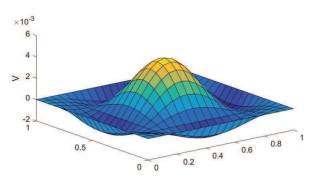
图 3
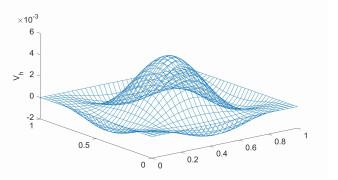
图 4
6 结论
参考文献
Nature of spatial chaos
DOI:10.1103/PhysRevLett.58.431 [本文引用: 1]
Bistable systems with propagating fronts leading to pattern foration
DOI:10.1103/PhysRevLett.60.2641 [本文引用: 3]
Dynamical velocity selection: marginal stability
DOI:10.1103/PhysRevLett.58.2571
Front propagation into unstable states: marginal stability as a dynamical mechanism for velocity selection
DOI:10.1103/PhysRevA.37.211 [本文引用: 1]
Orthogonal cubic spline collocation method for the extended Fisher-Kolmogorov equation
DOI:10.1016/j.cam.2004.04.002 [本文引用: 1]
A direct implementation of a modified boundary integral formulationation for the extended Fisher-Kolmogorov equation
DOI:10.4236/jamp.2015.310155 [本文引用: 1]
Finite element methods for one dimensional fourth order semilinear partial differential equation
DOI:10.1007/s40819-015-0068-0 [本文引用: 1]
Finite difference discretization of the extended Fisher-Kolmogorov equation in two dimensions
On the
Numerical methods for the extended Fisher-Kolmogorov(EFK) equation
Mixed finite element methods for a fourth order reaction diffusion equation
DOI:10.1002/num.20679 [本文引用: 2]
A new linearized Crank-Nicolson mixed element scheme for the extended Fisher-Kolmogorov equation
Extended Fisher-Kolmogorov方程的一类低阶非协调混合有限元方法
A type of new lower order nonconforming mixed finite elements methods for the extended Fisher-Kolmogorov equation
EFK方程一个新的低阶非协调混合有限元方法的高精度分析
High accuracy analysis of a new low order nonconforming mixed finite element method for the EFK equation
关于Wilson元的最佳收敛阶
A remark on the optimal order of convergence of Wilson's nonconforming element
A convergengce condition for the quadrilateral Wilson element
DOI:10.1007/BF01405567 [本文引用: 2]
二阶问题的一个类Wilson非协调元
A nonconforming element like wilson's for second-order problems
Accuracy analysis for quasi-Wilson element
DOI:10.1016/S0252-9602(17)30730-0 [本文引用: 1]
Approximation of nonconforming Quasi-Wilson element for Sine-Gordon equations
DOI:10.4208/jcm.1212-m3897 [本文引用: 1]
Quasi-Wilson nonconforming element approximation for nonlinear dual phase lagging heat conduction equations
Superconvergence analysis and extrapolation of quasi-Wilson nonconforming finite element method for nonlinear Sobolev equations
DOI:10.1007/s10255-013-0216-4 [本文引用: 1]
Nonconforming quadrilateral finite element method for a class of nonlinear sine-Gordon equations
DOI:10.1016/j.amc.2013.03.008 [本文引用: 1]
Wilson元求解二阶椭圆问题的一种新格式
A new scheme of wilson element for second-order elliptic problems
A nonconforming scheme to solve the parabolic problem
DOI:10.1016/j.amc.2015.04.089 [本文引用: 4]
黏弹性方程的Wilson元收敛性分析
Convergence analysis of Wilson element for viscoelasticity type equations
抛物积分微分方程的Wilson元收敛性分析
Convergence analysis of Wilson element for parabolic integro-differential equation
Nonconforming mixed finite element approximation to the stationary Navier-Stokes equations on anisotropic meshes
DOI:10.1016/j.na.2009.02.047 [本文引用: 1]
发展型偏微分方程间断有限元方法的超收敛性
Superconvergence of discontinuous Galerkin methods for time-dependent partial differential equations