Extended Fisher-Kolmogorov方程的间断有限元分析

摘要/Abstract

摘要：

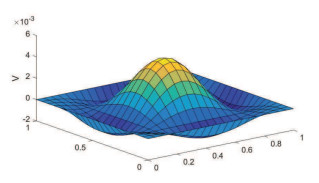
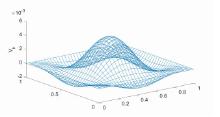
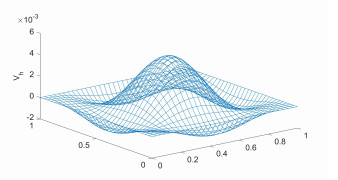
利用Wilson元研究了Extended Fisher-Kolmogorov（EFK）方程的间断有限元逼近格式.在不需要后处理技术的前提下，通过对非线性项采用新的分裂技术，分别得到了半离散和线性化欧拉全离散格式下原始变量$u$和中间变量$v=-\triangle u$的$O(h^{2})$和$O(h^{2}+\tau)$阶的收敛性结果，正好比通常的关于Wilson元的误差估计高出一阶.这里，$h$，$\tau$表示空间剖分参数和时间步长.

关键词: EFK方程, 间断有限元, Wilson元, 半离散和全离散格式, 收敛性

Abstract:

The discontinuous Galerkin finite element approximation schemes for the Extended Fisher-Kolmogorov (EFK) equation are studied by using the Wilson element. Without using the technique of postprocessing technique, the convergence results with order $O(h^{2})/O(h^{2}+\tau)$ for the primitive solution $u$ and intermediate variable $v=-\triangle u$ are obtained for the semi-discrete and linearized Euler fully discrete approximation schemes respectively through a new splitting technique for the nonlinear terms. The above results are just one order higher than the usual error estimates of the Wilson element. Here, $h$ and $\tau$ are parameters of the subdivision in space and time step, respectively.

Key words: EFK equation, Discontinuous Galerkin finite element, Wilson element, Semi-discrete and fully-discrete schemes, Convergence

中图分类号:

O242.21

杨晓侠,张厚超. Extended Fisher-Kolmogorov方程的间断有限元分析[J]. 数学物理学报, 2021, 41(6): 1880-1896.

Xiaoxia Yang,Houchao Zhang. Discontinuous Galerkin Finite Element Analysis of for the Extended Fisher-Kolmogorov Equation[J]. Acta mathematica scientia,Series A, 2021, 41(6): 1880-1896.

图/表 5

表 1

图 1

图 2

图 3

图 4

参考文献 33

1	Coullet P , Elphick C , Repaux D . Nature of spatial chaos. Physical Review Letters, 1987, 58 (5): 431- 434 doi: 10.1103/PhysRevLett.58.431
2	Dee G T , Van Saarloos W . Bistable systems with propagating fronts leading to pattern foration. Physical Review Letters, 1988, 60 (25): 2641- 2644 doi: 10.1103/PhysRevLett.60.2641
3	Van Saarloos W . Dynamical velocity selection: marginal stability. Physical Review Letters, 1987, 58 (24): 2571- 2574 doi: 10.1103/PhysRevLett.58.2571
4	Van Saarloos W . Front propagation into unstable states: marginal stability as a dynamical mechanism for velocity selection. Physical Review A, 1988, 37 (1): 211- 229 doi: 10.1103/PhysRevA.37.211
5	Danumjaya P , Pani A K . Orthogonal cubic spline collocation method for the extended Fisher-Kolmogorov equation. Journal of Computational and Applied Mathematics, 2005, 174 (1): 101- 117 doi: 10.1016/j.cam.2004.04.002
6	Onyejekwe O . A direct implementation of a modified boundary integral formulationation for the extended Fisher-Kolmogorov equation. Journal of Applied Mathematics and Physics, 2015, 3 (10): 1262- 1269 doi: 10.4236/jamp.2015.310155
7	Danumjaya P . Finite element methods for one dimensional fourth order semilinear partial differential equation. International Journal of Applied and Computational Mathematics, 2016, 2 (3): 395- 410 doi: 10.1007/s40819-015-0068-0
8	Khiari N , Omrani K . Finite difference discretization of the extended Fisher-Kolmogorov equation in two dimensions. Computers & Mathematics with Applications, 2011, 62 (11): 4151- 4160
9	He D D . On the $L^{\infty}$-norm convergence of a three-level linearly implicit finite difference method for the extended Fisher-Kolmogorov equation in both 1D and 2D. Computers & Mathematics with Applications, 2016, 71 (12): 2594- 2607
10	Liu F N, Zhao X P, Liu B. Fourier pseudo-spectral method for the extended Fisher-Kolmogorov equation in two dimensions. Advances in Difference Equations, 2017, Article number: 94
11	Danumjaya P , Pani A K . Numerical methods for the extended Fisher-Kolmogorov(EFK) equation. International Journal of Numerical Analysis and Modeling, 2006, 3 (2): 186- 210
12	Danumjaya P , Pani A K . Mixed finite element methods for a fourth order reaction diffusion equation. Numerical Methods for Partial Differential Equations, 2012, 28 (4): 1227- 1251 doi: 10.1002/num.20679
13	Wang J F , Li H , Siriguleng H , et al. A new linearized Crank-Nicolson mixed element scheme for the extended Fisher-Kolmogorov equation. The Scientific World Journal, 2013, 2013 (1): 202- 212
14	张厚超, 王俊俊, 石东洋. Extended Fisher-Kolmogorov方程的一类低阶非协调混合有限元方法. 数学物理学报, 2018, 38A (3): 571- 587
	Zhang H C , Wang J J , Shi D Y . A type of new lower order nonconforming mixed finite elements methods for the extended Fisher-Kolmogorov equation. Acta Mathematica Scientia, 2018, 38A (3): 571- 587
15	张厚超, 石东洋. EFK方程一个新的低阶非协调混合有限元方法的高精度分析. 高校应用数学学报, 2017, 32A (4): 437- 454
	Zhang H C , Shi D Y . High accuracy analysis of a new low order nonconforming mixed finite element method for the EFK equation. Applied Mathematics: A Journal of Chinese Universities, 2017, 32A (4): 437- 454
16	石钟慈. 关于Wilson元的最佳收敛阶. 计算数学, 1986, (2): 159- 163
	Shi Z C . A remark on the optimal order of convergence of Wilson's nonconforming element. Mathematica Numerica Sinica, 1986, (2): 159- 163
17	Shi Z C . A convergengce condition for the quadrilateral Wilson element. Numerische Mathematik, 1984, 44 (3): 349- 361 doi: 10.1007/BF01405567
18	江金生, 程晓良. 二阶问题的一个类Wilson非协调元. 计算数学, 1992, (3): 274- 278
	Jiang J S , Cheng X L . A nonconforming element like wilson's for second-order problems. Mathematica Numerica Sinica, 1992, (3): 274- 278
19	Chen S C , Shi D Y . Accuracy analysis for quasi-Wilson element. Acta Mathematica Scientia, 2000, 20 (1): 44- 48 doi: 10.1016/S0252-9602(17)30730-0
20	Shi D Y , Zhang D . Approximation of nonconforming Quasi-Wilson element for Sine-Gordon equations. Journal of Computational Mathematics, 2013, 31 (3): 271- 282 doi: 10.4208/jcm.1212-m3897
21	Shi D Y , Zhao Y M , Wang F L . Quasi-Wilson nonconforming element approximation for nonlinear dual phase lagging heat conduction equations. Applied Mathematics and Computation, 2014, 243 (17): 454- 464
22	Shi D Y , Wang F L , Zhao Y M . Superconvergence analysis and extrapolation of quasi-Wilson nonconforming finite element method for nonlinear Sobolev equations. Acta Mathematicae Applicatae Sinica, 2013, 29 (2): 403- 414 doi: 10.1007/s10255-013-0216-4
23	Shi D Y , Pei L F . Nonconforming quadrilateral finite element method for a class of nonlinear sine-Gordon equations. Applied Mathematics and Computation, 2013, 219 (17): 9447- 9460 doi: 10.1016/j.amc.2013.03.008
24	宋士仓, 苏恒迪, 雷蕾. Wilson元求解二阶椭圆问题的一种新格式. 高等学校计算数学学报, 2015, 37 (2): 156- 165
	Song S C , Su H D , Lei L . A new scheme of wilson element for second-order elliptic problems. Numerical Mathematics: A Journal of Chinese Universities, 2015, 37 (2): 156- 165
25	Song S C , Sun M , Jiang L Y . A nonconforming scheme to solve the parabolic problem. Applied Mathematics and Computation, 2015, 265, 108- 119 doi: 10.1016/j.amc.2015.04.089
26	Douglas J, Dupont T. Interior Penalty Procedures for Elliptic and Parabolic Galerkin Methods. Berlin: Springer, 1976
27	杨晓侠, 李永献. 黏弹性方程的Wilson元收敛性分析. 应用数学, 2018, 31 (3): 513- 521
	Yang X X , Li Y X . Convergence analysis of Wilson element for viscoelasticity type equations. Mathematica Applicata, 2018, 31 (3): 513- 521
28	梁聪刚, 杨晓侠, 石东洋. 抛物积分微分方程的Wilson元收敛性分析. 数学物理学报, 2019, 39A (5): 1158- 1169
	Liang C G , Yang X X , Shi D Y . Convergence analysis of Wilson element for parabolic integro-differential equation. Acta Mathematica Scientia, 2019, 39A (5): 1158- 1169
29	Shi D Y , Ren J C . Nonconforming mixed finite element approximation to the stationary Navier-Stokes equations on anisotropic meshes. Nonlinear Analysis: TMA, 2009, 71 (9): 3842- 3852 doi: 10.1016/j.na.2009.02.047
30	Hale J K. Ordinary Diffrential Equations. New York: Wiley-Interscience, 1969
31	张铁. 间断有限元理论与方法. 北京: 科学出版社, 2012
	Zhang T . The Theory and Method of Discotinuous Finite Element. Beijing: Science Press, 2012
32	孟雄, 舒期望, 杨扬. 发展型偏微分方程间断有限元方法的超收敛性. 中国科学, 2015, 45 (7): 1041- 1060
	Meng X , Shu Q W , Yang Y . Superconvergence of discontinuous Galerkin methods for time-dependent partial differential equations. Scientia Sinica Mathematica, 2015, 45 (7): 1041- 1060
33	曹外香, 张智民. 解一维双曲守恒律方程和抛物方程的间断有限元法的逐点和区间平均值误差估计. 中国科学, 2015, 45 (8): 1115- 1132
	Cao W X , Zhang Z M . Point-wise and cell average error estimates of the DG and LDG methods for 1D hyperbolic and parabolic equations. Scientia Sinica Mathematica, 2015, 45 (8): 1115- 1132

$m^{2}$	$\left\\| {u^{n}-U_h^{n} } \right\\|_h $	收敛阶	$\left\\| {v^{n}-V_h^{n} } \right\\|_h $	收敛阶
$4^{2}$	0.000046035	—	0.005970921	—
$8^{2}$	0.000012875	1.8381	0.001790764	1.7374
$16^{2}$	0.000003264	1.9799	0.000472460	1.9223
$32^{2}$	0.000000793	2.0417	0.000117908	2.0025
$64^{2}$	0.000000195	2.0240	0.000029285	2.0094

[1]	陈华鑫,贾文生. 群体博弈的逼近定理及通有收敛性[J]. 数学物理学报, 2021, 41(5): 1566-1573.
[2]	邓海云,刘辉,宋文静. 临界Schrödinger映射非齐次初边值问题的有限差分格式[J]. 数学物理学报, 2021, 41(5): 1311-1322.
[3]	谢亚君. 一类基于Halley-Newton型的有效修正算法[J]. 数学物理学报, 2021, 41(4): 1066-1078.
[4]	马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847.
[5]	万升联. 解变分不等式的一种二次投影算法[J]. 数学物理学报, 2021, 41(1): 237-244.
[6]	葛志昊,李瑞华. Bogoliubov-Tolmachev-Shirkov模型临界温度和能隙解的数值方法[J]. 数学物理学报, 2020, 40(6): 1699-1711.
[7]	王娟,原子霞. 具有对数敏感度和混合边界的一维趋化模型解的整体存在性和收敛性[J]. 数学物理学报, 2020, 40(6): 1646-1669.
[8]	李伟,黄鹏展. 流体相互作用模型的粘性分离有限元方法[J]. 数学物理学报, 2020, 40(5): 1362-1380.
[9]	杨柳,邓醉茶. 退化抛物型方程的一个初值反演问题[J]. 数学物理学报, 2020, 40(4): 891-903.
[10]	马国栋. 一般约束极大极小优化问题一个强收敛的广义梯度投影算法[J]. 数学物理学报, 2020, 40(3): 641-649.
[11]	何泽荣,张智强,裘哲勇. 一类非线性年龄等级结构种群模型的数值解法[J]. 数学物理学报, 2020, 40(2): 515-526.
[12]	梁聪刚,杨晓侠,石东洋. 抛物积分微分方程的Wilson元收敛性分析[J]. 数学物理学报, 2019, 39(5): 1158-1169.
[13]	章茜,蔡光辉. WOD随机变量序列的完全收敛性和矩完全收敛性[J]. 数学物理学报, 2019, 39(5): 1183-1191.
[14]	章志华,陈平炎. $φ$-混合序列加权和的完全收敛性[J]. 数学物理学报, 2018, 38(6): 1095-1102.
[15]	赵雅迪, 吴立飞, 杨晓忠, 孙淑珍. 时间分数阶慢扩散方程的一类有效差分方法[J]. 数学物理学报, 2018, 38(6): 1122-1134.