自从地球上出现了细胞和生物体, 自然界就有了大量的物种, 这些物种使自然界丰富多彩. 物种为了进化和生存, 总是会与其他物种产生联系, 包括种群竞争, 捕食-被捕食, 互惠共生等. 这些联系影响着物种的生存, 决定着群落和生态系统的稳定性. 因此, 研究种群之间的关系是很有必要的. 众所周知, 捕食者与食饵的相互作用是种群系统中最重要, 最常见的关系之一, 也是生态学家和生物学家关注的热点问题, 参见文献[1-8].

功能反应在捕食者-食饵系统^[9-18] 和流行病系统^[19-21] 的研究中起着非常重要的作用. 它表示捕食者在单位时间内杀死食饵的数量, 描述了不同营养水平之间的生物转移量. 1975年, Crowley和Martin^[22]提出了Crowley-Martin型功能反应函数$ P(x, y) = \frac{bx(t)y(t)}{(1+\alpha x(t))(1+\beta y(t))} $, 这是一种既依赖于捕食者又依赖于食饵的功能反应函数. 功能反应函数考虑了捕食者之间的相互作用, 假设即使食饵的种群密度很大, 捕获量仍会随着捕食者密度的增加而减少. 它与典型的Beddington-DeAngelis型功能反应函数相似, 但是在分母中包含了许多反映捕食者之间相互干扰的项. 当$ \alpha = \beta = 0 $时, Crowley-Martin型功能反应函数被简化为Holling I型功能反应函数, 当$ \beta = 0 $时, 其变为Holling II型功能反应函数. 另外, 无论捕食者是否在寻找猎物, Crowley-Martin型功能反应函数都允许捕食者之间存在干扰. 从这个角度来看, 它优于Beddington-DeAngelis型功能反应函数, 并且与自然界中的生物现象更加一致. 因此, 研究具有Crowley-Martin型功能反应函数的捕食者-食饵系统将会更好.

事实上, 自然界的生物种群很容易受到外部环境因素的干扰, 如温度、光照、暴雨和人为干预. 这些随机因素会以各种不同的方式对模型的几乎所有参数产生严重的影响. 因此, 研究随机环境下的种群动力学系统的动力学行为更具价值. 近年来, 种群动力学研究引起了人们的广泛关注, 为保护物种多样性提供了崭新的视角, 参见文献[23-28]. 2019年, 吕等^[29]建立了下面的具有环境噪声和Crowley-Martin型函数响应的捕食者-食饵系统

(1.1) $ \begin{eqnarray} \left\{\begin{array}{ll} {\rm d}x(t) = x(t)\left(a-x(t)-\frac{by(t)}{(1+\alpha x(t))(1+\beta y(t))}\right){\rm d}t+\sigma_1x(t){\rm d}B_1(t), \\ {\rm d}y(t) = y(t)\left(c-y(t)+\frac{fx(t)}{(1+\alpha x(t))(1+\beta y(t))}\right){\rm d}t+\sigma_2y(t){\rm d}B_2(t), \\ \end{array}\right. \end{eqnarray} $

其中, $ x(t) $和$ y(t) $分别代表食饵种群和捕食者种群的大小, $ B_1 $和$ B_2 $分别表示完全概率空间$ (\Omega, {\cal F}, {\Bbb P}) $上的布朗运动. 系统(1.1)中参数的生物学意义如表 1所示.

在随机系统中, 即使是微弱的噪声也可能导致动力学发生质变. 对于随机流, 即使在二维情况下, 基于Kolmogorov-Fokker-Planck方程的一般数学描述在技术上也非常困难. 因此, 使用渐近性和近似是合理的. 建设性方法之一是基于随机敏感性函数和置信域, 参见文献[30-33].

注意到, 对于系统(1.1)吕等^[29]给出了两个种群的持久性. 特别地, 他们指出该系统存在一个遍历的平稳分布. 然而, 有两个关键问题被忽视了: (ⅰ) 捕食者灭绝的条件是什么? 当捕食者的数量趋于灭绝时, 食饵的数量如何变化? (ⅱ) 捕食者-食饵系统的动力学能像确定性系统那样通过阈值来区分吗?

该文旨在改进和优化吕等^[29]的结果, 提出了一个阈值参数来研究随机系统(1.1) 的动力学. 结果表明: (ⅰ) 当$ \lambda<0 $时, 捕食者种群趋于灭绝, 而食饵种群的解弱收敛于一个唯一的不变概率分布; (ⅱ) 当$ \lambda>0 $时, 随机系统具有一个唯一的遍历平稳分布. 此外, 提出了随机敏感性分析方法来观察噪声对随机捕食者-食饵系统动力学的影响.

引理2.1^[34]   考虑以下一维模型

(2.1) $ \begin{eqnarray} {\rm d}\tilde{x}(t) = \tilde{x}(t)\left(a-\tilde{x}(t)\right){\rm d}t+\sigma_1\tilde{x}(t){\rm d}B_1(t), \; \tilde{x}(0) = x(0). \end{eqnarray} $

(ⅰ) 当$ \alpha\leq\frac{1}{2}\sigma_1^2 $时, 有$ \lim\limits_{t\rightarrow \infty}\tilde{x}(t) = 0\; \; {\rm a.s.}; $

(ⅱ) 当$ \alpha>\frac{1}{2}\sigma_1^2 $时, 随机过程$ \tilde{x} $存在一个唯一的不变概率测度(IPM) $ \pi(\cdot) $. 此外有$ \lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t\frac{\tilde{x}(s)}{1+\alpha \tilde{x}(s)}{\rm d}s = \int_0^\infty\frac{\nu}{1+\alpha\nu}\pi({\rm d}\nu)\; \; {\rm a.s.}, $和$ \lim\limits_{t\rightarrow \infty}\frac{\ln \tilde{x}(t)}{t} = 0\; \; {\rm a.s.} $.

为了研究随机系统(1.1)的动力学, 定义

$ \lambda = c-\frac{1}{2}\sigma_2^2+\int_0^\infty\frac{f\nu}{1+\alpha\nu}\pi({\rm d}\nu). $

令$ {\cal B}({\Bbb R}_+^{n}) $为$ {\Bbb R}_+^{n} $的Borel可测子集, 空间$ ({\Bbb R}_+^{n}, {\cal B}({\Bbb R}_+^{n})) $上的总变异范数$ \|\cdot, \cdot\|_{TV} $被定义为$ \|\varphi, \psi\|_{TV} = \sup\limits_{A\in{\cal B}({\Bbb R}_+^{n})}|\varphi(A)-\psi(A)|. $

定理2.2 假设$ \alpha>\frac{1}{2}\sigma_1^2 $, 则对任意初值$ (x(0), y(0))\in{\Bbb R}_+^{2, o} $:

(ⅰ) 当$ \lambda<0 $时, 捕食者$ y(t) $的数量以概率1指数收敛到0, 而食饵$ x(t) $的水平会弱收敛到IPM $ \pi(\cdot) $.

(ⅱ) 当$ \lambda>0 $, 解$ (x(t), y(t)) $存在一个唯一的IPM$ \varphi\in{\Bbb R}_+^{2, o} $, 这表明系统(1.1)是遍历的. 而且

$ \lim\limits_{t\rightarrow \infty}\|P(t, x, y, \cdot)-\varphi(\cdot)\|_{TV} = 0, \; (x, y)\in{\Bbb R}^{2, o}_+. $

证  (Ⅰ) 情形$ \lambda<0 $. 根据伊藤公式可得

(2.2) $ \begin{eqnarray} {\rm d}\ln y = \left(c-\frac{1}{2}\sigma_1^2-y+\frac{fx}{(1+\alpha x)(1+\beta y)}\right){\rm d}t+\sigma_2{\rm d}B_2(t). \end{eqnarray} $

由此可见

(2.3) $ \begin{eqnarray} \frac{\ln y(t)}{t} = c-\frac{1}{2}\sigma_2^2+\frac{1}{t}\int_0^t\left(\frac{fx(s)}{(1+\alpha x(s))(1+\beta y(s))}-y(s)\right){\rm d}s+\frac{\sigma_2B_2(t)}{t}+\frac{\ln y(0)}{t}. \end{eqnarray} $

因为

$ \lim\limits_{t\rightarrow \infty}\frac{\sigma_2B_2(t)+\ln y(0)}{t} = 0, $

则有

(2.4) $ \begin{eqnarray} \limsup\limits_{t\rightarrow \infty}\frac{\ln y(t)}{t}& = &c-\frac{1}{2}\sigma_2^2+\limsup\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t\left(\frac{fx(s)}{(1+\alpha x(s))(1+\beta y(s))}-y(s)\right){\rm d}s\\ & \leq&c-\frac{1}{2}\sigma_2^2+\limsup\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t\frac{fx(s)}{1+\alpha x(s)}{\rm d}s. \end{eqnarray} $

根据随机比较定理有

(2.5) $ \begin{eqnarray} \limsup\limits_{t\rightarrow \infty}\frac{\ln y(t)}{t} \leq c-\frac{1}{2}\sigma_2^2+\int_0^\infty\frac{f\nu}{1+\alpha\nu}\pi({\rm d}\nu) = \lambda<0\; \; {\rm a.s.}. \end{eqnarray} $

令$ \Omega_\epsilon = \left\{\omega:\ln y(t)\leq\frac{\lambda t}{2}\right\} $, $ \epsilon>0 $是任意的. 根据(2.5)式, 选择$ T>0 $使得

$ {\Bbb P}(\Omega_\epsilon)>1-\epsilon, \; \forall t\geq T. $

对$ \ln \tilde{x}(t)-\ln x(t) $应用伊藤公式得

(2.6) $ \begin{eqnarray} \ln\tilde{x}(t)-\ln x(t)& = &\int_{T}^t(x(s)-\tilde{x}(s)){\rm d}s+\int_{T}^t\frac{by(s)}{(1+\alpha x(s)(1+\beta y(s))}{\rm d}s\\ & \leq&b\int_{T}^ty(s){\rm d}s\leq-\frac{2b}{\lambda}{\rm e}^{\frac{\lambda T}{2}}. \end{eqnarray} $

选择$ T>\frac{2}{\lambda}\ln\left\{-\frac{\lambda\epsilon}{2b}\right\} $, 则有

(2.7) $ \begin{eqnarray} {\Bbb P}\{|\ln\tilde{x}(t)-\ln x(t)|>\epsilon\}\leq1-{\Bbb P}(\Omega_\epsilon)<\epsilon, \; \; \forall\; t\geq T. \end{eqnarray} $

假设$ \ln\tilde{x}(t) $的分布是$ \pi^*(\cdot) $. 定义函数$ g(\cdot):{\Bbb R}\mapsto{\Bbb R} $使得

$ |g(\omega_1)-g(\omega_2)|\leq|\omega_1-\omega_2|, \; |g(\omega_1)|<1, \; \forall \omega_1, \omega_2\in{\Bbb R}. $

根据Portmanteau定理, $ x(t) $弱收敛到$ \pi(\cdot) $, 前提是

(2.8) $ \begin{eqnarray} {\Bbb E}g(\ln x(t))\rightarrow \bar{g}: = \int_{\Bbb R}g(\omega)\pi^*({\rm d}\omega) = \int_0^\infty g(\ln \omega)\pi({\rm d}\omega), \; \; t\rightarrow \infty. \end{eqnarray} $

因为$ \pi(\cdot) $是$ \tilde{x}(t) $的分布, 则

(2.9) $ \begin{eqnarray} \lim\limits_{t\rightarrow \infty}{\Bbb E}g(\ln\tilde{x}(t)) = \bar{g}. \end{eqnarray} $

由此可见

(2.10) $ \begin{eqnarray} |{\Bbb E}g(\ln x(t))-\bar{g}| &\leq&|{\Bbb E}(g\ln x(t))-{\Bbb E}g(\ln\tilde{x}(t))|+|{\Bbb E}g(\ln \tilde{x}(t))-\bar{g}|\\ & \leq&\epsilon{\Bbb P}\{|\ln x(t)-\ln\tilde{x}(t)|\leq\epsilon\}+2{\Bbb P}\{|\ln x(t)-\ln \tilde{x}(t)|>\epsilon\}\\ & &+|{\Bbb E}g(\ln\tilde{x}(t))-\bar{g}|. \end{eqnarray} $

根据(2.7), (2.9)和(2.10)式得

$ \limsup\limits_{t\rightarrow \infty}|{\Bbb E}g(\ln x(t))-\bar{g}|\leq3\epsilon. $

因为$ \epsilon $是任意的, 所以(2.8)式成立.

(Ⅱ) 情形$ \lambda>0 $. 对$ V = \ln x+\frac{1}{f}\ln y $应用伊藤公式得

(2.11) $ \begin{eqnarray} {\rm d}V(t) = LV(x(t), y(t)){\rm d}t+\sigma_1{\rm d}B_1(t)+\frac{\sigma_2}{f}{\rm d}B_2(t), \end{eqnarray} $

其中

$ \begin{eqnarray*} LV(x, y)& = &a-\frac{1}{2}\sigma_1^2-x-\frac{by}{(1+\alpha x)(1+\beta y)}+\frac{1}{f}\left(c-\frac{1}{2}\sigma_2^2- y\right)+\frac{y}{(1+\alpha x)(1+\beta y)}\\ & \geq&a-\frac{1}{2}\sigma_1^2-x-by+\frac{1}{f}\left(c-\frac{1}{2}\sigma_2^2-y\right)+\frac{y}{(1+\alpha x)(1+\beta y)}\\ & = &a-\frac{1}{2}\sigma_1^2-\tilde{x}+(\tilde{x}-x)-by+\frac{1}{f}\left(c-\frac{1}{2}\sigma_2^2+\frac{f\tilde{x}} {1+\alpha\tilde{x}}-y\right)\\ & &-\left(\frac{\tilde{x}}{1+\alpha\tilde{x}}-\frac{x}{1+\alpha x}\right)-\left(\frac{x}{1+\alpha x} -\frac{x}{(1+\alpha x)(1+\beta y)}\right)\\ & \geq&a-\frac{1}{2}\sigma_1^2-\tilde{x}+\frac{1}{f}\left(c-\frac{1}{2}\sigma_2^2+ \frac{f\tilde{x}}{1+\alpha\tilde{x}}\right)-\left(b+\frac{1}{f}+\frac{\beta}{\alpha}\right)y. \end{eqnarray*} $

对方程(2.11)关于$ t $从$ 0 $到$ t $进行积分得

(2.12) $ \begin{eqnarray} \lim\limits_{t\rightarrow \infty}\frac{V(t)}{t}&\geq&\lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t\left (a-\frac{1}{2}\sigma_1^2-\tilde{x}(s)\right){\rm d}s +\frac{1}{f}\lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^t\left(c-\frac{1}{2}\sigma_2^2+\frac{f\tilde{x}(s)} {1+\alpha\tilde{x}(s)}\right){\rm d}s\\ & &-\left(b+\frac{1}{f}+\frac{\beta}{\alpha}\right) \lim\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^ty(s){\rm d}s+\lim\limits_{t\rightarrow \infty}\frac{1}{t}\left( \sigma_1B_1(t)+\frac{\sigma_2}{f}B_2(t)\right)\\ & &+\lim\limits_{t\rightarrow \infty}\frac{V(0)}{t}\; \; {\rm a.s.}. \end{eqnarray} $

因为

$ \lim\limits_{t\rightarrow \infty}\frac{V(0)}{t} = 0, \; \lim\limits_{t\rightarrow \infty}\frac{1}{t}\left(a-\frac{1} {2}\sigma_1^2-\tilde{x}(s)\right){\rm d}s = 0, \; \lim\limits_{t\rightarrow \infty}\frac{1}{t}\left(\sigma_1B_1(t) +\frac{\sigma_2}{f}B_2(t)\right) = 0\; \; {\rm a.s.} $

和

$ \lim\limits_{t\rightarrow \infty}\frac{V(t)}{t}\leq0\; \; {\rm a.s.}, $

可以推导得

$ \liminf\limits_{t\rightarrow \infty}\frac{1}{t}\int_0^ty(s){\rm d}s\geq\frac{\alpha\lambda}{\alpha bf+\alpha+\beta f}>0\; \; {\rm a.s.}. $

剩下的证明类似于文献[34]中定理2.2的标准论证.

注2.3(生物学意义) (ⅰ) 李雅普诺夫指数$ \lambda $代表捕食者的增长率. 当$ \lambda<0 $时, 捕食者种群的增长率为负, 种群逐渐死亡. 此外, 食饵种群的分布弱收敛到正IPM $ \pi(\cdot) $, 这表明食饵种群是持久的. (ⅱ) 当$ \lambda>0 $时, 捕食者的增长率为正, 并且系统的解存在一个唯一的遍历平稳分布, 这表明两种群共存.

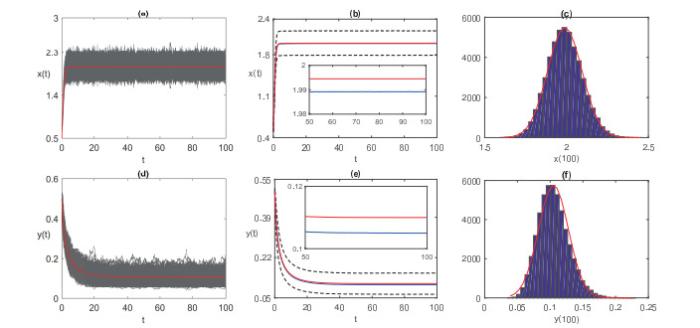
接下来, 给出两个例子来验证定理2.1的结果, 并说明随机噪声对捕食者-食饵种群相互作用的影响. 针对随机模型(1.1)和相应的确定型模型(即$ \sigma_i = 0, i = 1, 2 $)选择以下参数: $ a = 2 $, $ b = 0.1 $, $ c = 0.1 $, $ f = 0.01 $, $ \alpha = 0.4 $和$ \beta = 1 $.

例2.4 首先, 研究较小强度的噪声对随机系统(1.1)的动力学影响. 令$ \sigma_1 = \sigma_2 = 0.1 $, 经过5万次Matlab数值仿真, 得到图 1所示结果, 其中红色实线表示相应的确定性模型的解$ (x(t), y(t)) $. 在图 1(a)和1(d)中, 灰色实线代表随机模型(1.1)的解$ (x(t), y(t)) $的5万条样本轨迹. 可以看出随机模型的解$ (x(t), y(t)) $在确定性模型解的周围波动. 在图 1(b)和1(e)中, 蓝色实线表示随机解$ (x(t), y(t)) $的5万次样本轨迹的样本均值. 可以看出在时间$ t = 100 $时, 随机解$ (x(t), y(t)) $的样本均值为$ (1.989, 0.105) $, 这比确定性模型解$ (x(t), y(t)) $的值更小. 此外, 灰色虚线表示5万个样本在95%置信度时的置信区间. 可以看到5万个样本在时间$ t = 100 $时的置信区间和方差分别为$ [1.791, 2.202]\times[0.065, 0.155] $和$ 1.110536e-02\times5.256447e-04 $. 图 1(c)和1(f)展示了随机模型(1.1)有一个平稳分布.

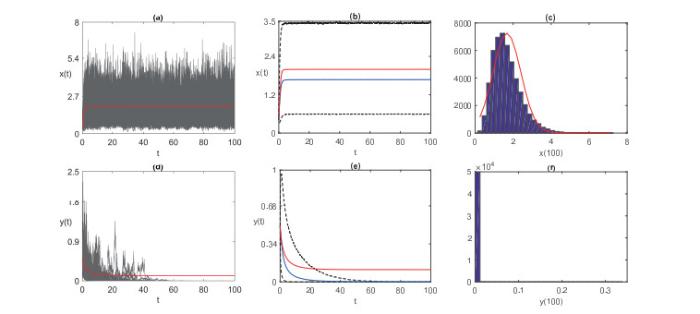
例2.5 现在, 研究较大强度的噪声对随机系统(1.1)的动力学影响. 令$ \sigma_1 = \sigma_2 = 0.8 $. 经过5万次Matlab数值仿真, 得到图 2所示结果, 其中红色实线表示相应的确定性情况的解$ (x(t), y(t)) $. 在图 2(a)和2(d)中, 灰色实线代表随机模型(1.1)的解的5万条样本轨迹. 可以看出随机模型的解$ x(t) $在确定性模型解的周围波动, 然而, 随机模型的解$ y(t) $却逐渐接近于0. 在图 2(b)和2(e)中, 蓝色实线表示随机解$ (x(t), y(t)) $的5万次样本轨迹的样本均值. 可以看出在时间$ t = 100 $时, 随机解$ (x(t), y(t)) $的样本均值为$ (1.672, 0) $, 这比确定性模型解$ (x(t), y(t)) $的值更小. 此外, 灰色虚线表示5万个样本在95%置信度时的置信区间. 可以看到5万个样本在时间$ t = 100 $时的置信区间和方差分别为$ [0.59, 3.444]\times[0, 0] $和$ 5.475314e-01\times1.793364e-04 $. 图 2(c)和2(f)展示了在$ t = 100 $时随机解的5万个样本的分布.

我们总结例2.4和例2.5的生物学意义如下.

1) 小的噪声抑制种群的大小, 使种群大小浮动在一定范围之内. 从图 1中可以看出, 当随机噪声的强度较小时, 随机模型的解在相应的确定性模型解的周围浮动, 而且随机解的样本均值小于确定性模型解的值. 此外, 图 1(e)和1(f)展示了随机模型(1.1)有一个平稳分布.

2) 大的噪声导致种群灭绝. 由图 2可以看出, 确定性模型的解是持久的, 而当噪声强度较大时, 随机模型的解$ y $变为0, 这说明较大的随机噪声会导致种群的灭绝.

在该节中, 使用文献[30-33, 35] 中的方法对随机模型(1.1)进行随机敏感性分析. 首先研究确定性模型的平衡点的稳定性, 即$ \sigma_i = 0, i = 1, 2 $的情形. 在没有随机噪声的情况下, 随机模型(1.1)变成了如下的确定性模型

(3.1) $ \begin{eqnarray} \left\{\begin{array}{ll} \frac{{\rm d}x(t)}{{\rm d}t} = x(t)\left(a-x(t)-\frac{by(t)}{(1+\alpha x(t))(1+\beta y(t))}\right), \\ \frac{{\rm d}y(t)}{{\rm d}t} = y(t)\left(c-y(t)+\frac{fx(t)}{(1+\alpha x(t))(1+\beta y(t))}\right). \end{array}\right. \end{eqnarray} $

接下来, 参考吕等在文献[29]中的参数, 即$ a = 0.6, b = 0.1, c = 0.3, f = 0.35, \alpha = 0.4, $$ \beta = 1 $对随机模型(1.1)进行随机敏感性分析. 首先提出一个定理来说明确定性模型(3.1)的平衡点的存在性和稳定性.

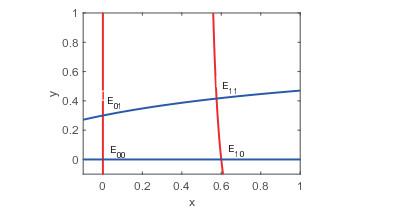
定理3.1 (平衡点的存在性和稳定性) 根据上述参数, 确定性模型(3.1)有三个边界平衡点和一个内部平衡点, 即$ E_{00}(0, 0) $, $ E_{01}(0, 0.3) $, $ E_{10}(0.6, 0) $, $ E_{11}(0.5761, 0.4758) $, 此外还有

(1) 确定型模型(3.1)在点$ E_{00} $的不稳定流形是$ W^u(E_{00}) = 2 $, 即边界平衡点$ E_{00} $是一个原点, 因此不稳定;

(2) 确定性模型(3.1)在点$ E_{01} $的稳定和不稳定流形分别是$ W^s(E_{01}) = 1 $和$ W^u(E_{01}) = 1 $, 即边界平衡点$ E_{01} $是一个鞍点, 因此不稳定;

(3) 确定性模型(3.1)在点$ E_{10} $的稳定和不稳定流形分别是$ W^s(E_{10}) = 1 $和$ W^u(E_{10}) = 1 $, 即边界平衡点$ E_{10} $是一个鞍点, 因此不稳定;

(4) 确定性模型(3.1)在点$ E_{11} $的稳定流形是$ W^s(E_{11}) = 2 $, 即内部平衡点$ E_{11} $是一个结点, 因此是局部渐近稳定的.

证  确定性模型(3.1)的平衡点应满足以下条件

(3.2) $ \begin{equation} \begin{array}{ll} 0 = x(t)\left(a-x(t)-\frac{by(t)}{(1+\alpha x(t))(1+\beta y(t))}\right), \\ 0 = y(t)\left(c-y(t)+\frac{fx(t)}{(1+\alpha x(t))(1+\beta y(t))}\right). \end{array} \end{equation} $

通过解方程(3.2), 可知确定性模型(3.1)有三个边界平衡点$ E_{00} $, $ E_{01} $, 和$ E_{10} $, 而且确定性模型(3.1)的内部平衡点应该是方程(3.2)的正根. 通过Matlab数值模拟发现确定性模型(3.1)在第一象限只有一个内部平衡点$ E_{11}(0.5761, 0.4157) $, 见图 3.

下面分析确定性模型(3.1)平衡点的稳定性. 为了方便研究, 设为模型(3.1)对应的平衡点为$ E^\#(x^\#, y^\#) $. 在点$ E^\# $相应的雅可比矩阵的取值为

$ \begin{eqnarray*} J(E^\#) = \left( \begin{array}{cc} a-2x^\#-\frac{by^\#}{(1+\alpha x^\#)^2(1+\beta y^\#)} & -\frac{bx^\#}{(1+\alpha x^\#)(1+\beta y^\#)^2}\\ \frac{fy^\#}{(1+\alpha x^\#)^2(1+\beta y^\#)}& c-2y^\#+\frac{fx^\#}{(1+\alpha x^\#)(1+\beta y^\#)^2} \end{array}\right). \end{eqnarray*} $

因此, 确定性模型(3.1)在$ E_{00} $处的特征值取值为$ \lambda_1(E_{00}) = a>0 $和$ \lambda_2(E_{00}) = c>0 $. 也就是说, 确定性模型(3.1)在点$ E_{00} $的不稳定流形是$ W^u(E_{00}) = 2 $, 即边界平衡点$ E_{00} $是不稳定. 情形(2)、(3)、(4)的证明与情形(1)的证明非常相似, 所以在此省略.

现在使用文献[35]中的方法对随机模型(1.1)进行随机敏感性分析, 该方法由与噪声强度$ \sigma_i, i = 1, 2 $和置信概率$ p $有关的置信椭圆方程给出. 在给出该定理之前, 先推导置信椭圆方程. 考虑下面的一般非线性随机系统

(3.3) $ \begin{eqnarray} \dot{x} = f(x)+\varepsilon \sigma(x) \dot{w}. \end{eqnarray} $

式中, $ x $是$ n $维向量, $ f(x) $是$ n $维向量函数, $ \sigma(x) $是$ n \times n $矩阵值函数, $ w(t) $是$ n $维维纳过程, $ \varepsilon $是噪声强度的标量参数. 假设相应的确定性系统$ (\varepsilon = 0) $具有指数稳定的吸引子.

强制系统(3.3)的随机轨迹离开了一个确定性吸引子, 并形成一个相应的具有平稳概率分布$ \rho(x, \varepsilon) $的随机吸引子, 该随机吸引子是对应的福克-普朗克方程的平稳解. 从技术上讲, 很难获得这样的解. 对于弱噪声, 采用了文献[36]中基于拟势$ v(x) = -\lim\limits_{\varepsilon \rightarrow 0} \varepsilon^{2} \log \rho(x, \varepsilon) $的渐近性. 对于较小的噪声强度, $ \rho(x, \varepsilon) $的近似可以写为

(3.4) $ \begin{eqnarray} \rho(x, \varepsilon) \approx K \cdot \exp \left(-\frac{v(x)}{\varepsilon^{2}}\right). \end{eqnarray} $

为了近似$ v(x) $, 使用文献[37]中的随机敏感性函数. 首先考虑随机强制平衡点. 假设$ \varepsilon = 0 $时的确定性系统(3.3)有一个指数稳定的平衡点$ \overline{x} $. 在这种情况下, 利用拟势$ v(x) \approx \frac{1}{2}(x-\overline{x}, V(x-\overline{x})) $的二次逼近, 可以得到高斯形式下平稳分布的渐近性

(3.5) $ \begin{eqnarray} \rho(x, \varepsilon) \approx K \cdot \exp \left(-\frac{\left(x-\overline{x}, W^{-1}(x-\overline{x})\right)}{2 \varepsilon^{2}}\right), \end{eqnarray} $

其中, $ \varepsilon^{2} W = \varepsilon^{2} V^{-1} $是协方差矩阵, 随机敏感性矩阵$ W $是下面矩阵方程的唯一解.

(3.6) $ \begin{eqnarray} {F W+W F^{\top} = -S, \quad F = \frac{\partial f}{\partial x}(\overline{x})}, {S = G G^{\top}, \quad G = \sigma(\overline{x})}. \end{eqnarray} $

该矩阵描述了随机系统(3.3)在确定性平衡点$ \overline{x} $周围的平稳分布随机状态的空间排列和大小. 利用该矩阵可以构造随机吸引子几何描述的置信域. 对于二维情形, 置信椭圆方程如下

(3.7) $ \begin{eqnarray} \left(x-\overline{x}, W^{-1}(x-\overline{x})\right) = 2 k^{2} \varepsilon^{2}, \end{eqnarray} $

式中, $ \varepsilon $表示噪声强度, $ k^{2} = -\ln (1-p) $, $ p $是置信概率. 设$ \mu_{1}, \mu_{2} $为特征值, 且$ \mu_{1}, \mu_{2} $为随机敏感性矩阵$ W $的归一化特征向量. 因为坐标$ z_{1} = \left(x-\overline{x}, u_{1}\right) $, $ z_{2} = \left(x-\overline{x}, u_{2}\right) $所以置信椭圆方程可以写成标准形式

(3.8) $ \begin{eqnarray} \frac{z_{1}^{2}}{\mu_{1}}+\frac{z_{2}^{2}}{\mu_{2}} = 2 k^{2} \varepsilon^{2}. \end{eqnarray} $

现在得到了置信椭圆方程的标准形式, 为了简单起见, 令$ \sigma_i = \sigma, i = 1, 2 $, 则有如下结果.

定理3.2 根据上述参数, 随机模型(1.1)的置信椭圆方程为

$ 3.4763(x-0.5761)^2-0.526(x-0.5761)(y-0.4157)+5.0628(y-0.4157)^2 = 2\sigma^2\ln\frac{1}{1-P}, $

其中$ \sigma $为随机噪声的强度, $ P $为置信概率.

证  定义$ W = \left( \begin{array}{cc} w_{11}\ &w_{12}\\ w_{21}\ &w_{22}\\ \end{array}\right) $为随机敏感性矩阵, 根据文献[35]得

(3.9) $ \begin{eqnarray} FW+WF^{\top} = -S, \end{eqnarray} $

式中, 雅可比矩阵$ F $和扩散矩阵$ S $分别表示如下

$ \begin{eqnarray*} F = \left( \begin{array}{cc} a-2x-\frac{by}{(1+\alpha x)^2(1+\beta y)} & -\frac{bx}{(1+\alpha x)(1+\beta y)^2}\\ \frac{fy}{(1+\alpha x)^2(1+\beta y)}& c-2y+\frac{fx}{(1+\alpha x)(1+\beta y)^2} \end{array}\right), \; \; S = \left( \begin{array}{cc} x^2&0\\ 0&y^2\\ \end{array}\right). \end{eqnarray*} $

通过解方程(3.9), 可得随机敏感性矩阵在$ E_{11}(0.5761, 0.4758) $处的值为

$ \begin{eqnarray*} W = \left( \begin{array}{cc} 0.2897 & 0.0148\\ 0.0148 & 0.1944\\ \end{array}\right). \end{eqnarray*} $

则置信概率为$ P $的置信椭圆方程是

$ \begin{eqnarray*} & &\langle(x-0.5761, y-0.4157)', W^{-1}((x-0.5761, y-0.4157)')\rangle = 2\sigma^2\ln\frac{1}{1-P}\\ &\Rightarrow &3.4653(x-0.5761)^2-0.5276(x-0.5761)(y-0.4157)+5.1641(y-0.4157)^2\\ & = &2\sigma^2\ln\frac{1}{1-P}. \end{eqnarray*} $

定理3.2证明完毕.

接下来, 给出一个例子来说明上面的结果.

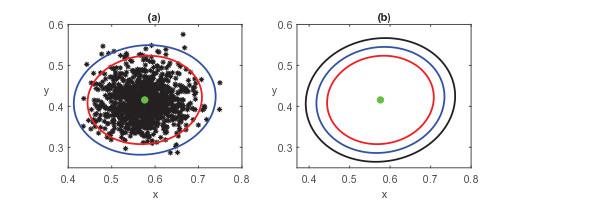
例3.3 使用参数$ a = 0.6 $, $ b = 0.1 $, $ c = 0.3 $, $ f = 0.35 $, $ \alpha = 0.4 $, $ \beta = 1 $. 通过Matlab数值仿真, 得到如图 4所示的结果. 在图 4(a)中, 黑色星号表示随机模型(1.1)在$ T = 1000 $时刻运行1000次后得到的1000个随机变量的随机状态, 绿点表示相应的确定性模型(3.1)的稳定内部平衡点$ E_{11} $, 红色实线和蓝色实线分别表示置信概率为95%和99%情况下的置信椭圆. 在图 4(b)中, 绿点表示相应的确定性模型(3.1)的稳定内部平衡点$ E_{11} $, 红色实线、蓝色实线、黑色实线分别表示置信概率$ P = 95\% $时, 噪声强度分别为$ \sigma = 0.1 $, $ 0.12 $, 和$ \sigma = 0.14 $时的置信椭圆. 数值结果表明

(1) 在没有噪声的情况下, 置信椭圆变为一个点, 即确定性模型(3.1)的稳定内部平衡点$ E_{11} $. 在噪声存在的情况下, 随着噪声强度的增大, 置信椭圆的半径逐渐增大, 确定性模型(3.1)的内部平衡点$ E_{11} $始终处于置信椭圆的中心位置. 这意味着在一定情况下, 较大的噪声会导致随机模型(1.1)的解在确定性模型(3.1)的解附近波动, 且波动幅度与噪声强度呈正相关.

(2) 随着置信概率的增加(从95%增加到99%), 置信椭圆中包含的样本也越来越多. 这说明在实际应用中, 要使统计结果更加准确, 应选择合理的置信概率.

文章研究了一类具有Crowley-Martin型函数响应的随机捕食者-食饵模型. 结果表明, 捕食者-食饵模型的随机动力学可以通过一个关键参数$ \lambda $来确定: 当$ \lambda<0 $时, 捕食者种群趋于灭绝, 食饵种群的解弱收敛到一个不变的概率分布; 然而当$ \lambda>0 $时, 随机系统存在一个唯一的遍历平稳分布.

此外, 提出了随机敏感性分析方法来观察噪声对随机捕食者-食饵系统动力学的影响. 研究结果表明, 较小强度的噪声可以抑制种群规模的扩大, 而较大强度的噪声则会导致种群的灭绝. 与此同时, 通过Matlab数值模拟得到如下结果: 在没有噪声的情况下, 置信椭圆变成为一个点, 这是确定性模型(3.1)的稳定的内部平衡点$ E_{11} $. 在噪声存在的情况下, 较大的噪声会导致随机模型(1.1)的解在确定性模型(3.1)的解周围波动, 且波动幅度与噪声强度呈正相关.

本文改进了吕等^[29]的结果, 提出了一个能确定随机系统(1.1)长期动力学的参数. 与其他带有Holling II型^[37-38]或者Beddington-DeAngelis型^[39-40]函数响应的随机系统相比, 带有Crowley-Martin型函数响应的随机系统(1.1)是以上系统的一种丰富和发展. 该方法对其他随机系统, 如随机HCV系统^[41] 和随机恒化器系统^[42]也是有效的.