具有Crowley-Martin型功能反应的捕食者-食饵模型的复杂动力学和随机敏感性分析

摘要/Abstract

摘要：

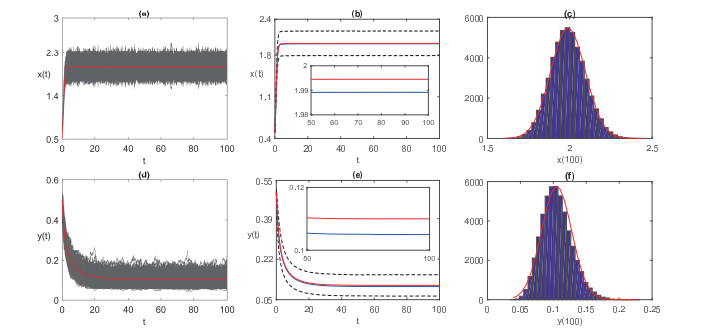
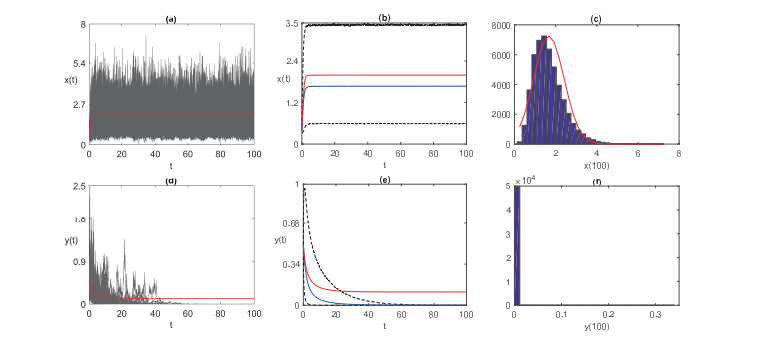
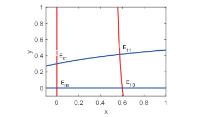
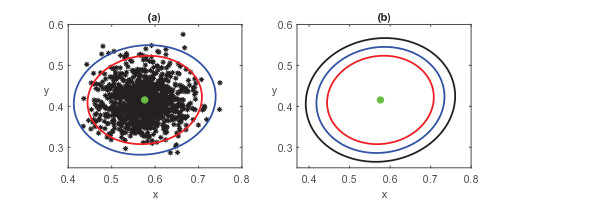
捕食者与食饵的相互作用在保护物种多样性方面起着关键作用.该文提出了一个具有Crowley-Martin型功能反应的随机捕食者-食饵模型.结果表明，当$λ$ < 0时，捕食者种群有灭绝的趋势，食饵种群的解弱收敛到一个不变的概率分布.当$λ$>0时，发现随机系统存在唯一一个遍历平稳分布.此外，该文还提出了随机敏感性分析方法来研究噪声对捕食者-食饵种群动力学的影响.研究结果表明，较小强度的噪声可以抑制种群规模的扩大，而较大强度的噪声则会导致种群的灭绝.

关键词: 捕食者-食饵相互作用, 随机模型, 随机敏感性分析, 遍历性, 平稳分布

Abstract:

Predator-prey interactions serve a pivotal role in protecting species diversity. In this study, the parameter $λ$ is presented to show the stochastic dynamics of a predator-prey model. The results show that the predator population tends to become extinct if $λ$ < 0. Furthermore, the solution of the prey population converges weakly to an invariant probability distribution. If $λ$>0, we find that the stochastic system admits a unique ergodic stationary distribution. In addition, stochastic sensitivity analysis is proposed to study the effects of noise on the dynamics of predator-prey populations. Our findings suggest that small-intensity noise can suppress population size enlargement, while large-intensity noise can lead to the extinction of populations.

Key words: Predator-prey interaction, Stochastic model, Stochastic sensitivity analysis, Ergodic property, Stationary distribution

中图分类号:

O175

王腾飞,冯涛,孟新柱. 具有Crowley-Martin型功能反应的捕食者-食饵模型的复杂动力学和随机敏感性分析[J]. 数学物理学报, 2021, 41(4): 1192-1203.

Tengfei Wang,Tao Feng,Xinzhu Meng. Complex Dynamics and Stochastic Sensitivity Analysis of a Predator-Prey Model with Crowley-Martin Type Functional Response[J]. Acta mathematica scientia,Series A, 2021, 41(4): 1192-1203.

图/表 5

表 1

图 1

图 2

图 3

图 4

参考文献 42

1	Kooi B , Ezio V . Ecoepidemic predator-prey model with feeding satiation, prey herd behavior and abandoned infected prey. Mathematical Biosciences, 2016, 274, 58- 72 doi: 10.1016/j.mbs.2016.02.003
2	Ai S , Du Y , Rui P . Traveling waves for a generalized Holling-Tanner predator-prey model. Journal of Differential Equations, 2017, 263, 7782- 7814 doi: 10.1016/j.jde.2017.08.021
3	Rao F , Carlos C , Kang Y . Dynamics of a diffusion reaction prey-predator model with delay in prey: Effects of delay and spatial components. Journal of Mathematical Analysis and Applications, 2018, 461, 1177- 1214 doi: 10.1016/j.jmaa.2018.01.046
4	Kang Y , Kumar S , Messan K . A two-patch prey-predator model with predator dispersal driven by the predation strength. Mathematical Biosciences & Engineering, 2017, 14, 843- 880
5	Wang H , Silogini T , Philippe G . Refuge-mediated predator-prey dynamics and biomass pyramids. Mathematical Biosciences, 2018, 298, 29- 45 doi: 10.1016/j.mbs.2017.12.007
6	Zhang F Q , Chen Y M , Li J Q . Dynamical analysis of a stage-structured predator-prey model with cannibalism. Mathematical Biosciences, 2019, 307, 33- 41 doi: 10.1016/j.mbs.2018.11.004
7	邓栋, 李燕. 一类带治疗项的非局部扩散SIR传染病模型的行波解. 数学物理学报, 2020, 40A (1): 72- 102 doi: 10.3969/j.issn.1003-3998.2020.01.008
	Deng D , Li Y . Traveling wave solutions of a nonlocal spreading SIR infectious disease model with treatment term. Acta Math Sci, 2020, 40A (1): 72- 102 doi: 10.3969/j.issn.1003-3998.2020.01.008
8	曹忠威, 文香丹, 冯微, 祖力. 一类具有随机扰动的非自治SIRI流行病模型的动力学行为. 数学物理学报, 2020, 40A (1): 221- 232 doi: 10.3969/j.issn.1003-3998.2020.01.017
	Cao Z W , Wen X D , Feng W , Zu L . Dynamic behavior of a nonautonomous SIRI epidemic model with random perturbations. Acta Math Sci, 2020, 40A (1): 221- 232 doi: 10.3969/j.issn.1003-3998.2020.01.017
9	Rajasekar S P , Pitchaimani M , Zhu Q X . Dynamic threshold probe of stochastic SIR model with saturated incidence rate and saturated treatment function. Physica A: Statistical Mechanics and its Applications, 2019, 535, 122300 doi: 10.1016/j.physa.2019.122300
10	Rajasekar S P , Pitchaimani M , Zhu Q X . Progressive dynamics of a stochastic epidemic model with logistic growth and saturated treatment. Physica A: Statistical Mechanics and its Applications, 2020, 538, 122649 doi: 10.1016/j.physa.2019.122649
11	Hu Z X , Ma W B , Ruan S G . Analysis of SIR epidemic models with nonlinear incidence rate and treatment. Mathematical Biosciences, 2012, 238, 12- 20 doi: 10.1016/j.mbs.2012.03.010
12	Qiu Z P , Michael Y , Shen Z . Global dynamics of an infinite dimensional epidemic model with nonlocal state structures. Journal of Differential Equations, 2018, 265, 5262- 5296 doi: 10.1016/j.jde.2018.06.036
13	Rajasekar S P , Pitchaimani M . Qualitative analysis of stochastically perturbed SIRS epidemic model with two viruses. Chaos, Solitons & Fractals, 2019, 118, 207- 221
14	Cai Y L , Kang Y , Banerjee M , Wang W M . A stochastic SIRS epidemic model with infectious force under intervention strategies. Journal of Differential Equations, 2015, 259, 7463- 7502 doi: 10.1016/j.jde.2015.08.024
15	Liu Q , Jiang D Q , Hayat T , Alsadi A . Stationary distribution of a stochastic delayed SVEIR epidemic model with vaccination and saturation incidence. Physica A: Statistical Mechanics and its Applications, 2018, 512, 849- 863 doi: 10.1016/j.physa.2018.08.054
16	Rajasekar S P , Pitchaimani M . Ergodic stationary distribution and extinction of a stochastic SIRS epidemic model with logistic growth and nonlinear incidence. Applied Mathematics and Computation, 2020, 377, 125143 doi: 10.1016/j.amc.2020.125143
17	Zhang X B , Zhang X H . The threshold of a deterministic and a stochastic SIQS epidemic model with varying total population size. Applied Mathematical Modelling, 2021, 91, 749- 767 doi: 10.1016/j.apm.2020.09.050
18	袁海龙, 王玉萍, 李艳玲. 一类带有交叉扩散的捕食-食饵模型的正解. 数学物理学报, 2019, 39A (3): 545- 559 doi: 10.3969/j.issn.1003-3998.2019.03.014
	Yan H L , Wang Y P , Li Y L . Positive solution of a predator-prey model with cross diffusion. Acta Math Sci, 2019, 39A (3): 545- 559 doi: 10.3969/j.issn.1003-3998.2019.03.014
19	Liu M , Du C , Deng M . Persistence and extinction of a modified Leslie-Gower Holling-type Ⅱ stochastic predator-prey model with impulsive toxicant input in polluted environments. Nonlinear Analysis: Hybrid Systems, 2018, 27, 177- 190 doi: 10.1016/j.nahs.2017.08.001
20	Zhuo X L , Zhang F X . Stability for a new discrete ratio-dependent predator-prey system. Qualitative Theory of Dynamical Systems, 2018, 17 (1): 189- 202 doi: 10.1007/s12346-017-0228-1
21	王双明, 樊馨蔓, 张明军, 梁俊荣. 具周期性潜伏期的SEIR传染病模型的动力学. 数学物理学报, 2020, 40A (2): 527- 539 doi: 10.3969/j.issn.1003-3998.2020.02.023
	Wang S M , Fan X M , Zhang M J , Liang J R . Dynamics of a SEIR infectious disease model with periodic incubation periods. Acta Math Sci, 2020, 40A (2): 527- 539 doi: 10.3969/j.issn.1003-3998.2020.02.023
22	Crowley P H , Martin E K . Functional responses and interference within and between year classes of a dragony population. Journal of the North American Benthological Society, 1989, 8, 211- 221 doi: 10.2307/1467324
23	Wang W M , Cai Y L , et al. Periodic behavior in a FIV model with seasonality as well as environment fluctuations. Journal of the Franklin Institute, 2017, 354 (16): 7410- 7428 doi: 10.1016/j.jfranklin.2017.08.034
24	Wu S , Shi J , Wu B . Global existence of solutions and uniform persistence of a diffusive predator-prey model with prey-taxis. Journal of Differential Equations, 2016, 260 (7): 5847- 5874 doi: 10.1016/j.jde.2015.12.024
25	Ghosh B , Zhdanova O L , Barman B , Frisman E Y . Dynamics of stage-structure predator-prey systems under density-dependent effect and mortality. Ecological Complexity, 2020, 41, 100812 doi: 10.1016/j.ecocom.2020.100812
26	Feng T , Qiu Z P . Global analysis of a stochastic TB model with vaccination and treatment. Discrete & Continuous Dynamical Systems-B, 2019, 24 (6): 2923- 2939
27	Xu C , Yuan S L , Zhang T H . Average break-even concentration in a simple chemostat model with telegraph noise. Nonlinear Analysis: Hybrid Systems, 2018, 29, 373- 382 doi: 10.1016/j.nahs.2018.03.007
28	Durrett R . Stochastic Calculus: A Practical Introduction. Boca Raton, FL: CRC Press, 1996
29	Lv J L , Liu H , Zou X L . Stationary distribution and persistence of a stochastic predator-prey model with a functional response. Journal of Applied Analysis and Computation, 2019, 9 (1): 1- 11
30	Bashkirtseva I , Ryashko L . Analysis of excitability for the FitzHugh-Nagumo model via a stochastic sensitivity function technique. Physical Review E, 2011, 83, 061109 doi: 10.1103/PhysRevE.83.061109
31	Bashkirtseva I , Ryashko L , Zaitseva S . Analysis of nonlinear stochastic oscillations in the biochemical Goldbeter model. Communications in Nonlinear Science and Numerical Simulation, 2019, 73, 165- 176 doi: 10.1016/j.cnsns.2019.02.008
32	Bashkirtseva I , Ryashko L . Stochastic sensitivity and variability of glycolytic oscillations in the randomly forced Sel'kov model. European Physical Journal B, 2017, 90 (1): 17
33	Bashkirtseva I , Ryashko L . Analysis of noise-induced phenomena in the nonlinear tumor-immune system. Physica A: Statistical Mechanics and its Applications, 2020, 549, 123923
34	Du N H , Nguyen D H , Yin G G . Conditions for permanence and ergodicity of certain stochastic predator-prey models. Journal of Applied Probability, 2016, 53 (1): 187- 202
35	Bashkirtseva I , Ryazanova T , Ryashko L . Confidence domains in the analysis of noise-induced transition to chaos for Goodwin model of business cycles. International Journal of Bifurcation and Chaos, 2014, 24, 1440020
36	Freidlin M I , Wentzell A D . Random Perturbations of Dynamical Systems. New York: Springer-Verlag, 1984
37	Bashkirtseva I , Ryashko L B . Sensitivity and chaos control for the forced nonlinear oscillations. Chaos, Solitons & Fractals, 2005, 26, 1437- 1451
38	Liu Z W , Shi N Z , Jiang D Q , Ji C Y . The asymptotic behavior of a stochastic Predator-Prey system with Holling Ⅱ functional response. Abstract and Applied Analysis, 2012, 2012, 1- 14
39	Qiu H , Liu M , Wang K , Wang Y . Dynamics of a stochastic predator-prey system with Beddington-DeAngelis functional response. Applied Mathematics and Computation, 2012, 219 (4): 2303- 2312
40	Cantrell R S , Cosner C . On the dynamics of Predator-Prey models with the Beddington-DeAngelis functional response. Journal of Mathematical Analysis and Applications, 2001, 257 (1): 206- 222
41	Feng T , Qiu Z P , Meng X Z . Stochastic hepatitis C virus system with host immunity. Discrete and Continuous Dynamical Systems Series B, 2019, 24 (12): 6367- 6385
42	Wang L , Jiang D Q . A note on the stationary distribution of the stochastic chemostat model with general response functions. Applied Mathematics Letters, 2017, 73, 22- 28

符号	生物学意义
$a$	在没有捕食的情况下, 食饵种群的内在增长率
$b$	攻击系数
$\alpha$	处理时间
$\beta$	捕食者个体之间的干扰程度
$c$	在没有捕食的情况下, 捕食者种群的内在增长率
$f$	捕食的转化率
$\sigma_i^2$	布朗运动$B_i$的强度$(i = 1, 2)$

[1]	蓝桂杰,付盈洁,魏春金,张树文. 具有Holling Ⅲ功能性反应的随机捕食食饵模型的平稳分布和周期解[J]. 数学物理学报, 2018, 38(5): 984-1000.
[2]	魏凤英, 林青腾. 一类具有校正隔离率随机SIQS模型的绝灭性与分布[J]. 数学物理学报, 2017, 37(6): 1148-1161.
[3]	张水利, 张绍义. 一般状态空间跳过程的遍历性[J]. 数学物理学报, 2014, 34(4): 859-878.
[4]	王健. 一般对称跳过程的Lyapunov漂移条件[J]. 数学物理学报, 2011, 31(3): 785-795.
[5]	唐有荣, 刘再明, 侯振挺. 广生灭过程的遍历性及平稳分布[J]. 数学物理学报, 1998, 18(1): 25-32.
[6]	陈金文. 有限维Brusseltor模型的正常返性[J]. 数学物理学报, 1995, 15(2): 121-125.