期权定价模型^[1]是目前为止对于期权定价最成功的模型, 其假定股票价格的变动由几何布朗运动描述. 但是, 对金融数据的实证研究已经表明, B-S期权定价模型不能很好的描述价格变化的一些特征, 诸如: 常值周期性、长相依性、厚尾倾斜的边缘分布等.

由于分数布朗运动可以描述资产价格长相依性的特征, 所以一些学者将B-S期权定价模型中的布朗运动替换为分数布朗运动, 进而得出了各类期权的定价公式. 但由于分数型的B-S定价公式已被证明在一个完备且无摩擦的市场上会产生套利^[2], 为了解决套利的问题以及体现资产价格变动过程中长相依性的特征, Cheridito^[3]建议使用混合分数布朗运动去描述金融资产价格的变动. Cheridito已经证明, 当Hurst指数$ H \in(3 / 4,1)$时, 混合分数布朗运动等价于布朗运动, 因而是无套利的. 此后, 混合分数布朗运动在金融衍生产品定价中被广泛使用. 但无论是假定标的资产价格由分数布朗运动还是混合分数布朗运动所驱动的随机微分方程描述, 均不能很好反映有些资产价格变动过程中出现的常值周期性的特征.

因此, 为了描述资产价格变动过程中出现的常值周期性、长相依性的特征, Magdziarz^[4]引入时变几何布朗运动描述资产价格的变动, 获得了时变几何布朗运动下的欧式期权定价公式, 并证明了他所采用的定价模型是无套利的. 时变过程, 在通俗意义上讲就是将随机过程状态发生的时间仍视为一个随机过程, 从而形成一个复合随机过程. 此后, Gu等^[5]研究了时变几何分数布朗运动下带有交易成本的欧式期权定价问题, 得到了欧式期权的定价公式; Guo等^[6]得到了时变混合分数布朗运动下欧式期权的定价公式; Shokrollahi等^[7]研究了时变混合分数布朗运动下带有交易成本的欧式期权以及货币期权的定价问题, 得到了相应的定价公式; Shokrollahi^[8]得到了当股票价格由时变混合分数布朗运动描述时几何平均亚式期权的定价公式, 并且获得了在一些特殊情形下亚式期权价格的下界.

以上关于时变情形下的定价模型大多集中于对于欧式期权的研究, 在对亚式期权定价研究中, 已有文献很少考虑到标的资产价格变动过程中呈现的常值周期性的特征. 另外, 已有关于亚式期权的定价模型也很少考虑标的资产交易过程中的交易成本, 这与金融市场实际不符. 因此, 为了体现资产价格变动的常值周期性、长相依性以及交易过程中产生的交易成本, 该文考虑时变混合分数布朗运动下带交易费用的几何平均亚式期权定价问题. 行文结构如下: 第二部分给出了相关的预备知识; 第三部分给出了期权定价模型以及几何平均亚式看涨期权价格所满足的偏微分方程; 第四部分推出了几何平均亚式看涨、看跌期权的定价公式; 第五部分为数值试验; 第六部分为实证分析; 第七部分为结论.

本节给出时变过程的相关概念、性质以及基本结论.

定义2.1^[9-10]  若$ \{U_\alpha(\tau)\}_{\tau\geq0} $为$ \alpha $ -稳定Lévy过程且严格递增, 则称首达时间过程

$ T_\alpha (t) = \inf \left\{ {\tau > 0:U_\alpha (\tau ) > t} \right\} $

为逆$ \alpha $ -稳定从属过程.

性质2.1^{[5, 9-10]}  过程$ \left\{ {U_\alpha (\tau )} \right\}_{\tau \ge 0} $具有如下性质

1) $ \left\{ {U_\alpha (\tau )} \right\}_{\tau \ge 0} $的Laplace变换为$ E\left( {e^{ - uU_\alpha (\tau )} } \right) = e^{ - \tau u^\alpha } $, $ \alpha \in (0, 1) $.

2) $ U_\alpha(t) $是$ \frac{1}{\alpha } $自相似的, $ T_\alpha(t) $是$ \alpha $自相似的, 即对于任意的$ c>0 $, 有

$ U_\alpha(ct) \mathop{ = }\limits^{\rm d} c^{\frac{1}{\alpha }}U_\alpha(t), \quad T_\alpha(ct) \mathop{ = }\limits^{\rm d} c^{\alpha}T_\alpha(t), $

其中$ \mathop{ = }\limits^{\rm d} $表示具有相同的分布.

定义2.2^[6-7]  考虑一个复合过程$ Z_\alpha(t) = B(T_\alpha(t)) $, $ Z_{\alpha, H}(t) = B_H(T_\alpha (t)) $, 其中$ B(\cdot) $表示标准布朗运动, $ B_H(\cdot) $表示分数布朗运动, 则称

$ M_{\alpha , H}(t) = M_{T_\alpha(t)}^H = Z_\alpha(t) + Z_{\alpha, H} (t). $

为时变混合分数布朗运动.

下面给出复合过程$ Z_\alpha(t) = B(T_\alpha(t)) $, $ Z_{\alpha, H}(t) = B_H(T_\alpha (t)) $相关的一些性质.

引理2.1^[5]  对于$ 0<\beta $, $ \beta _1 $, $ \beta _2<+\infty $以及$ n \in {\rm N} $, 有

1) $ o\left( {\chi ^{\beta _1 } } \right) \cdot o\left( {\chi ^{\beta _2 } } \right) = o\left( {\chi ^{\beta _1 + \beta _2 } } \right) $,

2) $ \left( {o\left( {\chi ^\beta } \right)} \right)^n = o\left( {\chi ^{n\beta } } \right) $,

3) $ o\left( {\chi ^{\beta _1 } } \right) + o\left( {\chi ^{\beta _2 } } \right) = o\left( {\chi ^{\min \{ \beta _1 , {\kern 1pt} \beta _2 {\kern 1pt} \} } } \right) $.

引理2.2^[5-7]  对于任意的$ \varepsilon \in (0, \alpha H) $, 有

$ \Delta T_\alpha(t) = o\left( {\Delta t^{\alpha - \varepsilon } } \right), \quad \Delta Z_{\alpha , H} (t) = o\left( {\Delta t^{\alpha H - \varepsilon } } \right). $

进一步, 对于$ n \in {\rm N} $, $ 0 \le s < t < + \infty $, 下列不等式成立

1) $ E\left( {\left| {T_\alpha (t) - T_\alpha (s)} \right|^n } \right) \le \frac{{n!}}{{\Gamma ^n (\alpha + 1)}}(t - s)^{\alpha n} $,

2) $ E\left( {\left| {Z_{\alpha , H} (t) - Z_{\alpha , H} (s)} \right|^n } \right) \le (n - 1)!!\left[ {\frac{{n!}}{{\Gamma ^n (\alpha + 1)}}} \right]^H (t - s)^{H\alpha n} $,

3) $ E\left( {\left| {Z_\alpha (t) - Z_\alpha (s)} \right|^n } \right) \le (n - 1)!!\left[ {\frac{{n!}}{{\Gamma ^n (\alpha + 1)}}} \right]^{\frac{1}{2}} (t - s)^{\frac{1}{2}\alpha n} $.

引理2.3^[5-7]  令$ \alpha \in \left( {\frac{1}{2}, {\kern 1pt} 1} \right) $且$ n \in N $, 对于任意的$ 0 < b \ne 1 $以及$ T > 0 $, 则$ b^{\left| {Z_{\alpha , H} (t)} \right|} $的$ n $阶矩存在, 并且$ b^{\left| {Z_{\alpha , H} (t)} \right|} $的任意阶矩在$ t \in \left[ {0, T} \right] $上一致有界.

下面给出时变过程矩的一些重要结论.

引理2.4^[5-7]  对于逆$ \alpha $ -稳定从属过程$ T_\alpha(t) $以及复合过程$ Z_{\alpha, H}(t) = B_H(T_\alpha(t)) $, 有

1) $ E\left( {T_\alpha ^m (t)} \right) = \frac{{t^{m\alpha } m!}}{{\Gamma (m\alpha + 1)}} $;

2) $ E\left( {\Delta T_\alpha (t)} \right) = \frac{1}{{\Gamma (\alpha + 1)}}\left[ {\left( {t + \Delta t} \right)^\alpha - t^\alpha } \right] = \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}\Delta t $;

3) $ E\left( {\left( {\Delta B_H \left( {T_\alpha (t)} \right)} \right)^2 } \right) = \left[ {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right]^{2H} \Delta t^{2H} $;

4) $ E\left( {\left( {\Delta B_H \left( {T_\alpha (t)} \right)} \right)} \right) = \sqrt {\frac{2}{\pi }} \left[ {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right]^H \Delta t^H $.

为了得到在离散情形下带有交易成本的几何平均亚式看涨期权的定价公式, 需要对金融市场做如下几点基本的假设.

1) 标的资产(股票)在时刻$ t $的价格$ S_t $服从下式

(3.1) $ \begin{equation} S_t = S_0 \exp \left\{ {\mu T_\alpha (t) + \sigma M_{\alpha , {\kern 1pt} H} (t)} \right\}, \ S_0 > 0, \end{equation} $

其中$ S_0 $, $ \mu $是常数, $ M_{\alpha , H}(t) = Z_\alpha(t) + Z_{\alpha, H}(t) $为时变混合分数布朗运动, 且$ \alpha $, $ H $满足$ \alpha \in \left( {\frac{1}{2}, 1} \right) $, $ H \in \left[ {\frac{1}{2}, 1} \right) $, $ 2\alpha - \alpha H > 1 $.

2) 在离散的时间点$ \Delta t, 2\Delta t, {\kern 1pt} 3\Delta t, {\kern 1pt} \cdots , T $才能买卖股票.

3) 买卖股票时需支付一定的交易成本, 即在股价为$ S_t $时有$ U $单位的股票买进$ \left( {U > 0} \right) $或卖出$ \left( {U < 0}\right) $, 则要产生$ \frac{k}{2}\left| U \right|S_t $的交易费用, 其中$ k > 0 $为常数, $ k $表示交易费率.

4) 股票无红利支付, 所有证券完全可分, 允许卖空.

5) 期权的价值可通过一个含有$ U(t) $单位的股票和一单位价值为$ F_t $的无风险债券的投资组合复制. 债券市场由下列微分方程描述

(3.2) $ \begin{equation} {\rm d}F_t = rF_t {\rm d}t, \end{equation} $

其中$ r $为无风险利率, 在时间点$ \Delta t, 2\Delta t, {\kern 1pt} 3\Delta t, {\kern 1pt} \cdots , T $, 期权的价值必须等于可复制投资组合的价值以减少套利机会.

基于上述假设, 推导在时间区间$ \left( {{\rm{0}}, t} \right] $上股票平均价格为$ J_t = e^{\frac{1}{t}\int_0^t {\ln S_\tau {\rm d}\tau } } $的几何平均亚式看涨期权价格所满足的偏微分方程. 令$ C = C\left( {t, S_t , J_t {\kern 1pt} {\kern 1pt} } \right) $为几何平均亚式看涨期权在时刻$ t $时股票价格为$ S_t $、股票平均价格为$ J_t $时的价格, 且$ C\left( {t, S_t , J_t {\kern 1pt} {\kern 1pt} } \right) $具有连续的偏导数.

定理3.1  假设在时刻$ t\left( {0 \le t \le T} \right) $股票价格$ S_t $服从(3.1)式, 则行权价格为$ K $、到期日为$ T $的几何平均亚式看涨期权在时刻$ t(0 \le t \le T) $的价格$ C = C(t, S_t , J_t ) $满足如下的偏微分方程

(3.3) $ \begin{equation} \frac{{\partial C}}{{\partial t}} + rS_t \frac{{\partial C}}{{\partial S_t }} + \frac{1}{2}\delta (t)^2 S_t^2 \frac{{\partial ^2 C}}{{\partial S_t^2 }} + \frac{{J_t \left( {\ln S_t - \ln J_t } \right)}}{t}\frac{{\partial C}}{{\partial J_t }} = rC, \end{equation} $

其中

$ \delta (t)^2 = \sigma ^2 \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}} + \sigma ^2 \left[ {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right]^{2H} \Delta t^{2H - 1} + k\sqrt {\frac{2}{\pi }\left( {\sigma ^2 \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}\Delta t^{ - 1} + \sigma ^2 \left( {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right)^{2H} \Delta t^{2H - 2} } \right)} , $

$ \Gamma ( \cdot ) $表示Gamma函数, 边界条件为$ C\left( {T, S_T , J_T {\kern 1pt} {\kern 1pt} } \right) = \max \left\{ {0, J_T - K{\kern 1pt} {\kern 1pt} } \right\} $.

证  在长度为$ \Delta t $的时间间隔$ \left[ {t, t + \Delta t} \right) $上, 股价$ S_t $的变化量为

(3.4) $ \begin{eqnarray} \Delta S_t& = & S_{t + \Delta t} - S_t = S_t \left( {e^{\mu \Delta T_\alpha (t) + \sigma \Delta M_{\alpha , H} (t)} - 1} \right){\kern 1pt}{}\\ & = & S_t \left( {\mu \Delta T_\alpha (t) + \sigma \Delta M_{\alpha , {\kern 1pt} H} (t) + \frac{1}{2}\left( {\mu \Delta T_\alpha (t) + \sigma \Delta M_{\alpha , H} (t)} \right)^2 } \right){}\\ & &+ \frac{1}{6}S_t e^{\theta \mu \Delta T_\alpha (t) + \theta \sigma \Delta M_{\alpha , H} (t)} \cdot \left( {\mu \Delta T_\alpha (t) + \sigma \Delta M_{\alpha , H} (t)} \right)^3, \end{eqnarray} $

其中$ \theta = \theta (t, \Delta t) \in (0, 1) $是依赖于$ S_t $的随机变量, 由$ M_{\alpha , H} (t) $的定义得

(3.5) $ \begin{eqnarray} \frac{1}{6}S_t e^{\theta \mu \Delta T_\alpha (t) + \theta \sigma \Delta M_{\alpha , H} (t)}& \le &\frac{1}{6}S_t e^{\mu \Delta T_\alpha (T)} \cdot e^{\sigma \left| {\Delta Z_\alpha (t)} \right|} \cdot e^{\sigma \left| {\Delta Z_{\alpha , H} (t)} \right|}{}\\ & \le &\frac{1}{6}S_t e^{\mu \Delta T_\alpha (T)} \cdot e^{\sigma \left| {Z_\alpha (t)} \right|} \cdot e^{\sigma \left| {Z_\alpha (t + \Delta t)} \right|}{}\\ & & \times e^{\sigma \left| {Z_{\alpha , H} (t)} \right|} \cdot e^{\sigma \left| {Z_{\alpha , H} (t + \Delta t)} \right|}, \end{eqnarray} $

因此, 对于$ n \in {\rm N} $, 有

(3.6) $ \begin{equation} E\left( {e^{n\mu T_\alpha (T)} } \right) = \sum\limits_{j = 0}^\infty {\frac{{(n\mu )^j }}{{j!}}E\left( {T_\alpha (T)} \right)^j } = \sum\limits_{j = 0}^\infty {\frac{{\left( {n\mu T^\alpha } \right)^j }}{{\Gamma (j\alpha + 1)}}} = E_\alpha \left( {n\mu T^\alpha } \right) < + \infty , \end{equation} $

其中$ E_\alpha \left( \cdot \right) $为Mittage-Lefller函数^[11], 根据引理2.1–2.3以及(3.6)式得

(3.7) $ \begin{equation} \Delta t^{2\varepsilon } \cdot \frac{1}{6}S_t e^{\theta \mu \Delta T_\alpha (t) + \theta \sigma \Delta M_{\alpha , H} (t)} = \Delta t^{2\varepsilon } \cdot \frac{1}{6}S_t e^{\theta \mu \Delta T_\alpha (t) + \theta \sigma \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right)} = o(\Delta t^\varepsilon ), \end{equation} $

由(3.4)–(3.7)式以及引理2.1得

(3.8) $ \begin{aligned}& \frac{1}{6} S_{t} e^{\theta \mu \Delta T_{\alpha}(t)+\theta \sigma \Delta M_{\alpha, H}(t)} \cdot\left(\mu \Delta T_{\alpha}(t)+\sigma \Delta M_{\alpha, H}(t)\right)^{3} \\=& \frac{1}{6} S_{t} e^{\theta \mu \Delta T_{\alpha}(t)+\theta \sigma\left(\Delta Z_{\alpha}(t)+\Delta Z_{\alpha, H}(t)\right)} \cdot\left(\mu \Delta T_{\alpha}(t)+\sigma\left(\Delta Z_{\alpha}(t)+\Delta Z_{\alpha, H}(t)\right)\right)^{3} \\=& \Delta t^{-2 \varepsilon} \cdot o\left(\Delta t^{\varepsilon}\right) \cdot\left(o\left(\Delta t^{\alpha-\varepsilon}\right)+o\left(\Delta t^{\alpha / 2-\varepsilon}\right)+o\left(\Delta t^{\alpha H-\varepsilon}\right)\right)^{3} \\=& o\left(\Delta t^{\frac{3 \alpha}{2}-4 \varepsilon}\right)=o(\Delta t)\end{aligned} $

那么

(3.9) $ \begin{eqnarray} \Delta S_t & = & \mu S_t \Delta T_\alpha (t) + \sigma S_t \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right){}\\ & & + \frac{1}{2}\sigma ^2 S_t \left( {\left( {\Delta Z_\alpha (t)} \right)^2 + \left( {\Delta Z_{\alpha , H} (t)} \right)^2 } \right) + o\left( {\Delta t} \right), \end{eqnarray} $

对$ C = C\left( {t, S_t , J_t {\kern 1pt} {\kern 1pt} } \right) $作Taylor展开, 得

(3.10) $ \begin{eqnarray} &&\Delta C\left( {t, S_t , J_t } \right){}\\ & = & \frac{{\partial C}}{{\partial t}}\Delta t + \frac{1}{2}\frac{{\partial ^2 C}}{{\partial t^2 }}\Delta t^2 + \frac{{\partial C}}{{\partial J_t }}\Delta J_t + \frac{1}{2}\frac{{\partial ^2 C}}{{\partial J_t^2 }}\Delta J_t^2 + \frac{{\partial C}}{{\partial S_t }}\Delta S_t+ \frac{1}{2}\frac{{\partial ^2 C}}{{\partial S_t^2 }}\Delta S_t^2 + o\left( {\Delta t^{\frac{\alpha }{2} + \alpha H - \varepsilon } } \right){}\\ & = & \frac{{\partial C}}{{\partial t}}\Delta t + \frac{{\partial C}}{{\partial J_t }}\Delta J_t + \frac{{\partial C}}{{\partial S_t }}\Delta S_t + \frac{1}{2}\frac{{\partial ^2 C}}{{\partial S_t^2 }}\Delta S_t^2 + o\left( {\Delta t} \right){}\\ & = & \frac{{\partial C}}{{\partial S_t }}\left( {\mu S_t \Delta T_\alpha (t) + \sigma S_t \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , {\kern 1pt} H} (t)} \right) + \frac{1}{2} \sigma ^2 S_t \left( {\left( {\Delta Z_\alpha (t)} \right)^2 + \left( {\Delta Z_{\alpha , H} (t)} \right)^2 } \right)} \right){\kern 1pt}{}\\ & & + \frac{1}{2}\frac{{\partial ^2 C}}{{\partial S_t^2 }} \left( {\sigma ^2 S_t^2 \left( {\Delta Z_\alpha (t)^2 + \Delta Z_{\alpha , {\kern 1pt} H} (t)^2 } \right)} \right) + \frac{{\partial C}}{{\partial t}}\Delta t + \frac{{\partial C}} {{\partial J_t }}\Delta J_t + o\left( {\Delta t} \right), \end{eqnarray} $

由(3.6)式以及文献[5], 可以验证$ \frac{{\partial ^3 C}}{{\partial S_t^3 }} $, $ \frac{{\partial ^2 C}}{{\partial C\partial t}} $, $ \frac{{\partial ^2 C}}{{\partial S_t \partial J_t }} $是$ o\left( {\Delta t^{\frac{1}{2}(1 - H\alpha ) - \varepsilon } } \right) $, 因此

(3.11) $ \begin{equation} \Delta \left( {\frac{{\partial C}}{{\partial S_t }}} \right) = \frac{{\partial ^2 C}}{{\partial S_t \partial t}}\Delta t + \frac{{\partial ^2 C}}{{\partial S_t^2 }}\Delta S_t + \frac{1}{2}\frac{{\partial ^3 C}}{{\partial S_t^3 }} \Delta S_t^2+ \frac{{\partial ^2 C}}{{\partial S_t \partial J_t }}\Delta J_t + o\left( {\Delta t} \right), \end{equation} $

(3.12) $ \begin{equation} \left| {\Delta \left( {\frac{{\partial C}}{{\partial S_t }}} \right)} \right|S_{t + \Delta t} = S_t^2 \left| {\frac{{\partial ^2 C}}{{\partial S_t^2 }}} \right|\left| {\sigma \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right)} \right| + o\left( {\Delta t} \right), \end{equation} $

由假设3)以及假设5), 投资组合$ \Pi _t $在$ \left[ {t, t + \Delta t} \right) $上的价值改变量为

(3.13) $ \begin{eqnarray} \Delta \Pi _t & = &U_t \Delta S_t + \Delta F_t - \frac{k}{2}\left| {\Delta U_t } \right|S_{t + \Delta t} {}\\ & = & U_t \Delta S_t + rF_t \Delta t - \frac{k}{2}\left| {\Delta U_t } \right|S_{t + \Delta t} + o\left( {\Delta t} \right), \end{eqnarray} $

其中$ U_t $在$ \left[ {t, {\kern 1pt} t + \Delta t} \right) $上是固定的常数.

由假设2)以及假设5), $ C\left( {t, S_t {\kern 1pt} , J_t } \right) $在时间点$ \Delta t, 2\Delta t, 3\Delta t, {\kern 1pt} \cdots , {\kern 1pt} T $上等于投资组合的价值, 即

(3.14) $ \begin{equation} C\left( {t, S_t , J_t } \right) = U_t S_t + F_t , \end{equation} $

取$ U_t = \frac{{\partial C}}{{\partial S_t }} $, 由(3.12)–(3.14)式得

(3.15) $ \begin{eqnarray} \Delta \Pi& = & \frac{{\partial C}}{{\partial S_t }}\left[ {\mu S_t \Delta T_\alpha (t) + \sigma S_t \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right) + \frac{1}{2}\sigma ^2 S_t \left( {\left( {\Delta Z_\alpha (t)} \right)^2 + \left( {\Delta Z_{\alpha , H} (t)} \right)^2 } \right)} \right]{}\\ & & + rF_t \Delta t - \frac{k}{2}\left| {\Delta \frac{{\partial C}}{{\partial S_t }}} \right|S_{t + \Delta t} + o\left( {\Delta t} \right){}\\ & = & \frac{{\partial C}}{{\partial S_t }}\left[ {\mu S_t \Delta T_\alpha (t) + \sigma S_t \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right) + \frac{1}{2}\sigma ^2 S_t \left( {\left( {\Delta Z_\alpha (t)} \right)^2 + \left( {\Delta Z_{\alpha , H} (t)} \right)^2 } \right)} \right]{}\\ & &+ rF_t \Delta t - \frac{k}{2}S_t^2 \left| {\frac{{\partial ^2 C}}{{\partial S_t^2 }}} \right|\left| {\sigma \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right)} \right| + o\left( {\Delta t} \right), \end{eqnarray} $

根据(3.10)式以及(3.15)式得

(3.16) $ \begin{eqnarray} \Delta \Pi - \Delta C& = & \left( {rC - rS_t \frac{{\partial C}}{{\partial S_t }} - \frac{{\partial C}}{{\partial t}} - \frac{{\partial C}}{{\partial J_t }} \cdot \frac{{\rm d}J_t }{{\rm d}t}} \right)\Delta t{}\\ & &- \frac{1}{2}\frac{{\partial ^2 C}}{{\partial S_t^2 }}\left( {\sigma ^2 S_t^2 \left( {\Delta Z_\alpha (t)^2 + \Delta Z_{\alpha , H} (t)^2 } \right)} \right){}\\ & &- \frac{k}{2}S_t^2 \left| {\frac{{\partial ^2 C}}{{\partial S_t^2 }}} \right|\left| {\sigma \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right)} \right| + o\left( {\Delta t} \right), \end{eqnarray} $

由(3.16)式以及假设5)得

(3.17) $ \begin{eqnarray} E\left( {\Delta \Pi - \Delta C} \right)& = & \left( {rC - rS_t \frac{{\partial C}}{{\partial S_t }} - \frac{{\partial C}}{{\partial t}} - \frac{{\partial C}}{{\partial J_t }} \cdot \frac{{\rm d}J_t }{{\rm d}t}} \right)\Delta t{}\\ & &- \left[ {\frac{1}{2}\frac{{\partial ^2 C}}{{\partial S_t^2 }}\left( {\sigma ^2 S_t^2 E\left( {\Delta Z_\alpha (t)^2 + \Delta Z_{\alpha , H} (t)^2 } \right)} \right)\Delta t^{ - 1} } \right]\Delta t{}\\ & &- \left[ {\frac{k}{2}\Delta t^{ - 1} S_t^2 \left| {\frac{{\partial ^2 C}}{{\partial S_t^2 }}} \right|E\left| {\sigma \left( {\Delta Z_\alpha (t) + \Delta Z_{\alpha , H} (t)} \right)} \right|} \right]\Delta t + o\left( {\Delta t} \right){}\\ & = & 0, \end{eqnarray} $

再根据引理2.4以及文献[7]可得

(3.18) $ \begin{eqnarray} rC & = & rS_t \frac{{\partial C}}{{\partial S_t }} + \frac{{\partial C}}{{\partial t}} + \frac{{\partial C}}{{\partial J_t }} \cdot \frac{{\rm d}J_t }{{\rm d}t}{\kern 1pt} {} \\ &&+ \frac{1}{2}\sigma ^2 S_t^2 \frac{{\partial ^2 C}}{{\partial S_t^2 }}\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}} + \frac{1}{2}\sigma ^2 S_t^2 \frac{{\partial ^2 C}}{{\partial S_t^2 }}\left[ {\frac{{t^{\alpha - 1} }} {{\Gamma (\alpha )}}} \right]^{2H} \Delta t^{2H - 1} {\kern 1pt} {}\\ &&+ \frac{k}{2}S_t^2 \left| {\frac{{\partial ^2 C}}{{\partial S_t^2 }}} \right|\sqrt {\frac{2}{\pi }\left( {\sigma ^2 \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}\Delta t^{ - 1} + \sigma ^2 \left( {\frac{{t^{\alpha - 1} }} {{\Gamma (\alpha )}}} \right)^{2H} \Delta t^{2H - 2} } \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \end{eqnarray} $

对于没有交易成本的普通欧式看涨期权, 总有$ \frac{{\partial ^2 C}}{{\partial S_t^2 }} > 0 $. 对于几何平均亚式看涨期权, 也作同样的假定, 令

$ \delta (t)^2 = \sigma ^2 \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}} + \sigma ^2 \left[ {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right]^{2H} \Delta t^{2H - 1} + k\sqrt {\frac{2}{\pi } \left( {\sigma ^2 \frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}\Delta t^{ - 1} + \sigma ^2 \left( {\frac{{t^{\alpha - 1} }}{{\Gamma (\alpha )}}} \right)^{2H} \Delta t^{2H - 2} } \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}, $

从而

(3.19) $ \begin{equation} rC = rS_t \frac{{\partial C}}{{\partial S_t }} + \frac{{\partial C}}{{\partial t}} + \frac{{\partial C}} {{\partial J_t }} \cdot \frac{{\rm d}J_t }{{\rm d}t} + \frac{1}{2}\delta (t)^2 S_t^2 \frac{{\partial ^2 C}}{{\partial S_t^2 }}, \end{equation} $

又因$ \frac{{\rm d}J_t }{{\rm d}t} = \frac{{J_t \left( {\ln S_t - \ln J_t } \right)}}{t} $, 带入(3.19)式可得

$ \frac{{\partial C}}{{\partial t}} + rS_t \frac{{\partial C}}{{\partial S_t }} + \frac{1}{2}\delta (t)^2 S_t^2 \frac{{\partial ^2 C}}{{\partial S_t^2 }} + \frac{{J_t \left( {\ln S_t - \ln J_t } \right)}} {t}\frac{{\partial C}}{{\partial J_t }} = rC. $

定理3.1证毕.

定理4.1  假设在时刻$ t\left( {0 \le t \le T} \right) $股票价格$ S_t $由(3.1)式刻画, 则行权价格为$ K $、到期日为$ T $的几何平均亚式看涨期权在时刻$ t(0 \le t \le T) $的价格$ C(t, S_t , J_t ) $为

(4.1) $ \begin{equation} C\left( {t, S_t , J_t } \right) = \left( {J_t^t S_t^{T - t} } \right)^{\frac{1}{T}} e^{\left( {\theta + \frac{{\omega ^2 }}{2} - r} \right)\left( {T - t} \right)} N\left( {d_1 } \right) - Ke^{ - r\left( {T - t} \right)} N\left( {d_2 } \right), \end{equation} $

其中

$ d_{1}=\frac{(1 / T) \ln \frac{J_{t}^{t} S_{t}^{T-t}}{K^{T}}+\left(\theta+\omega^{2}\right)(T-t)}{\omega \sqrt{T-t}}, \quad d_{2}=d_{1}-\omega \sqrt{T-t}$

$ \theta = \frac{1}{{T - t}}\int_t^T {\left( {r - \frac{{\delta (t)^2 }}{2}\frac{{T - \tau }}{T}} \right){\rm d}\tau } , \quad {\kern 1pt} \omega ^{\rm{2}} {\rm{ = }}\frac{1}{{T - t}}\int_t^T {\delta (t)^2 \left( {\frac{{T - \tau }}{T}} \right)^{\rm{2}} {\rm d}\tau } {\rm{.}} $

证  类似于文献[12]中的方法, 令

(4.2) $ \begin{equation} \varphi _t = \frac{{t\ln J_t + (T - t)\ln S_t }}{T}, \end{equation} $

(4.3) $ \begin{equation} C\left( {t, S_t , J_t } \right) = U(t, \varphi _t ), \end{equation} $

由(4.2)式以及(4.3)式可得

$ \frac{{\partial C}}{{\partial t}} = \frac{{\partial U}}{{\partial t}} + \frac{{\partial U}}{{\partial \varphi _t }} \frac{{\ln J_t - \ln S_t }}{T}, $

$ \frac{{\partial C}}{{\partial J_t }} = \frac{{\partial U}}{{\partial \varphi _t }} \frac{t}{{TJ_t }}, \ {\kern 1pt} \frac{{\partial C}}{{\partial S_t }} = \frac{{\partial U}}{{\partial \varphi _t }} \frac{{(T - t)}}{{TS_t }}, $

$ \frac{{\partial ^2 C}}{{\partial S_t^2 }} = \left[ {\frac{{T - t}}{{TS_t }}} \right]^2 \frac{{\partial ^2 U}}{{\partial \varphi _t^2 }} - \frac{{(T - t)}}{{TS_t^2 }}\frac{{\partial U}}{{\partial \varphi _t }}. $

将上述变换带入(3.3)式, 得

(4.4) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{{\partial U}}{{\partial t}} + \left( {r - \frac{1}{2}\delta (t)^{\rm{2}} } \right)\frac{{(T - t)}}{T}\frac{{\partial U}}{{\partial \varphi _t }} + \frac{1}{2}\delta (t)^{\rm{2}} \left[ {\frac{{T - t}}{T}} \right]^2 \frac{{\partial ^2 U}}{{\partial \varphi _t^2 }} = rU, \\ U(T, \varphi _T ) = \max \left\{ {e^{\varphi _T } - K, 0} \right\}. \end{array} \right. \end{equation} $

令

(4.5) $ \begin{equation} \tau = \gamma (t), \ \eta _\tau = \varphi _t + \alpha (t), \ X(\tau , \eta _\tau ) = U(t, \varphi _t )e^{\beta (t)} , \end{equation} $

其中$ \alpha (t) $, $ \beta (t) $, $ \gamma (t) $为待定函数, 则

(4.6) $ \begin{equation} \begin{array}{l} { } \frac{{\partial U}}{{\partial t}} = e^{ - \beta (t)} \left[ {\frac{{\partial X}}{{\partial \tau }}\gamma '(t) - \beta '(t)X + \frac{{\partial X}}{{\partial \eta _\tau }}\alpha '(t)} \right], \\ { } \frac{{\partial U}}{{\partial \varphi _t }} = e^{ - \beta (t)} \frac{{\partial X}}{{\partial \eta _\tau }}, \ {\kern 1pt} \frac{{\partial ^2 U}}{{\partial \varphi _t^2 }} = \frac{\partial }{{\partial \varphi _t }}\left( {e^{ - \beta (t)} \frac{{\partial X}}{{\partial \eta _\tau }}} \right) = e^{ - \beta (t)} \frac{{\partial ^2 X}}{{\partial \eta _\tau ^2 }}, \\ \end{array} \end{equation} $

将(4.6)式带入(4.4)式, 得

$ \gamma '(t)\frac{{\partial X}}{{\partial \tau }} + \left[ {\alpha '(t) + \left( {r - \frac{1}{2}\delta (t)^{\rm{2}} } \right)\frac{{T - t}}{T}} \right]\frac{{\partial X}}{{\partial \eta _\tau }} + \frac{1}{2}\delta (t)^{\rm{2}} \left( {\frac{{T - t}}{T}} \right)^2 \frac{{\partial ^2 X}}{{\partial \eta _\tau ^2 }} - (r + \beta '(t))X = 0, $

再令

$ \gamma '(t) + \frac{{\delta (t)^2 }}{{\sigma ^2 }}\left( {\frac{{T - t}}{T}} \right)^2 = 0, \ \alpha '(t) + \left( {r - \frac{1}{2}\delta (t)^{\rm{2}} } \right)\frac{{T - t}}{T} = 0, \ {\kern 1pt} r + \beta '(t) = 0, $

结合终止条件$ \alpha (T) = \beta (T) = \gamma (T) = 0 $, 解得

$ \alpha (t) = \int_t^T {\left( {r - \frac{{\delta (\tau )^2 }}{2}} \right)} \left( {\frac{{T - \tau }}{T}} \right){\rm d}\tau , \ \beta (t) = r\left( {T - t} \right), \ {\kern 1pt} \gamma (t) = \int_t^T {\frac{{\delta (\tau )^2 }}{{\sigma ^2 }}} \left( {\frac{{T - \tau }}{T}} \right)^2 {\rm d}\tau . $

在变换(4.5)下, (4.4)式转变为热传导方程的Cauchy问题

(4.7) $ \begin{equation} \left\{ \begin{array}{l} { } \frac{{\partial X}}{{\partial \tau }} = \frac{{\sigma ^2 }}{2}\frac{{\partial ^2 X}}{{\partial \eta _\tau ^2 }}, \\ X(0, \eta _0 ) = \max \left\{ {e^{\eta _0 } - K, 0} \right\}. \end{array} \right. \end{equation} $

其解可以表示成Poission公式, 即

(4.8) $ \begin{equation} X\left( {\tau , \eta _\tau } \right) = \frac{1}{{\sigma \sqrt {2\pi \tau } }}\int_{ - \infty }^{ + \infty } {\left( {e^y - K} \right)^ + e^{ - \frac{{(y - \eta _\tau )^2 }}{{2\sigma ^2 \tau }}} {\rm d}y}. \end{equation} $

由变换(4.2)式、(4.3)式以及(4.5)式, 回到原变量以及函数$ C\left( {t, S_t , J_t } \right) $, 可得

(4.9) $ \begin{eqnarray} X\left( {\tau , \eta _\tau } \right) & = & e^{\eta _\tau + \frac{{\sigma ^2 \tau }}{2}} N\left( {\frac{{\eta _\tau + \sigma ^2 \tau - \ln K}}{{\sigma \sqrt \tau }}} \right) - KN\left( {\frac{{\eta _\tau - \ln K}}{{\sigma \sqrt \tau }}} \right) {}\\ & = & \left( {J_t^t S_t^{T - t} } \right)^{\frac{1}{T}} e^{\left( {\theta + \frac{{\omega ^2 }}{2}} \right)\left( {T - t} \right)} N\left( {d_1 } \right) - KN\left( {d_2 } \right), \end{eqnarray} $

(4.10) $ \begin{equation} C\left( {t, S_t , J_t } \right) = \left( {J_t^t S_t^{T - t} } \right)^{\frac{1}{T}} e^{\left( {\theta + \frac{{\omega ^2 }}{2} - r} \right)\left( {T - t} \right)} N\left( {d_1 } \right) - Ke^{ - r\left( {T - t} \right)} N\left( {d_2 } \right), \end{equation} $

其中

$\begin{gathered}d_{1}=\frac{(1 / T) \ln \frac{J_{t}^{t} S_{t}^{T-t}}{K^{T}}+\left(\theta+\omega^{2}\right)(T-t)}{\omega \sqrt{T-t}}, \quad d_{2}=d_{1}-\omega \sqrt{T-t} \\\theta=\frac{1}{T-t} \int_{t}^{T}\left(r-\frac{\delta(t)^{2}}{2} \frac{T-\tau}{T}\right) \mathrm{d} \tau, \quad \omega^{2}=\frac{1}{T-t} \int_{t}^{T} \delta(t)^{2}\left(\frac{T-\tau}{T}\right)^{2} \mathrm{~d} \tau\end{gathered}$

定理4.1证毕.

推论4.1  假设在时刻$ t(0 \le t \le T) $股票价格$ S_t $由(3.1)式刻画, 则行权价格为$ K\rm{、} $到期日为$ T $的几何平均亚式看跌期权在时刻$ t(0 \le t \le T) $的价格$ P(t, S_t, J_t) $为

(4.11) $ \begin{equation} P\left( {t, S_t , J_t } \right) = Ke^{ - r\left( {T - t} \right)} N\left( { - d_2 } \right) - \left( {J_t^t S_t^{T - t} } \right)^{\frac{1}{T}} e^{\left( {\theta + \frac{{\omega ^2 }}{2} - r} \right)\left( {T - t} \right)} N\left( { - d_1 } \right), \end{equation} $

其中$ d_1 $, $ d_2 $, $ \theta $, $ \omega $与定理4.1中的$ d_1 $, $ d_2 $, $ \theta $, $ \omega $相同.

证  由边界条件$ P\left( {T, S_T , J_T {\kern 1pt} {\kern 1pt} } \right) = \max \left\{ {0, K - J_T {\kern 1pt} {\kern 1pt} } \right\} $, 运用定理4.1中的方法求解方程(3.3)可得看跌期权价格.

对亚式期权定价问题相关的研究近年来取得了很多成果, 例如: 分数布朗运动下的定价模型^[13]、混合分数布朗运动下的定价模型^[14]等. 结合本文在时变混合分数布朗运动下带交易成本的亚式期权定价模型, 下面对基于不同亚式期权定价模型下得到的期权价格作一比较, 结果如表 1所示.

各定价公式中一些参数取值如下: 无风险利率$ r = 0.05 $、红利率$ q = 0 $、波动率$ \sigma = 0.25 $、Hurst指数$ H = 0.75 $、到期日$ T = 1 $, 股票当前价格$ S_0 = 100 $. 在本文的定价公式中, 取$ \alpha = 0.8 $、交易费率$ k = 0.01 $、交易时间点之间的长度$ \Delta t = 0.1 $. 其中$ K $表示行权价格、$ C_{GBM} $表示几何布朗运动下几何平均亚式看涨期权的价格、$ C_{FBM} $表示分数布朗运动下几何平均亚式看涨期权的价格、$ C_{MFBM} $表示混合分数布朗运动下几何平均亚式看涨期权的价格, $ C_{TC - MFBM} $表示时变混合布朗运动下带交易成本的几何平均亚式看涨期权的价格.

各模型基本情况统计, 结果见表 2.

对于本文所得的几何平均亚式看涨期权的定价公式(4.1), 其中的参数$ \alpha $、Hurst指数$ H $与期权价格$ C $之间的关系如图 1所示. 其中, 取无风险利率$ r = 0.05 $、红利率$ q = 0 $、波动率$ \sigma = 0.25 $、Hurst指数$ H = 0.75 $、到期日$ T = 1 $、股票当前价格$ S_0 = 100 $、行权价格$ K = 100 $、交易费率$ k = 0.01 $, 交易时间点之间的长度$ \Delta t = 0.1 $.

由表 1可知, 基于不同定价模型的几何平均亚式看涨期权定价公式得到的期权价格没有特别显著的差异, 但与其它亚式期权定价公式给出的价格相比, 时变混合分数布朗运动下带有交易成本的定价公式得到的期权价格随着行权价格的升高, 期权价格具有更快的衰减速度, 这与交易过程中产生的交易费用相对应, 更低的价格是对交易成本累积的惩罚, 与金融市场流动性理论相一致. 图$ 1 $显示了对于不同的参数$ \alpha $, 随着Hurst指数$ H $的增大, 期权价格均降低, 并且$ \alpha $越大, 所对应的期权价格越小.

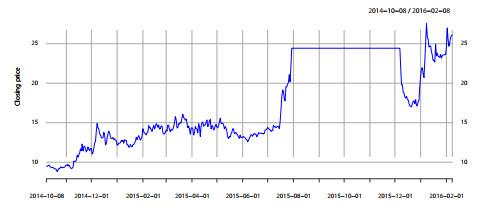
选取万科2014年10月8日至2016年9月30日的收盘价(数据来源于"yahoo") 来验证模型(3.1)在描述具有常值周期性特征的资产价格变动时是否具有有效性. 在选取的时间段上股价变动如图 2所示.

从中可以明显的看到在选取的时间区间内, 万科股价的变动显示出了类似于“常值周期性”的特征, 因此可以考虑运用模型(3.1)来描述这种变动.

首先运用历史数据估计股票价格的波动率以及运用$ {\rm{R/S}} $分析法估计Hurst指数$ H $.

波动率的估计式如下

(6.1) $ {\sigma _n} = \sqrt {\frac{1}{{m - 1}}\sum\limits_i^m {{{\left( {{u_{n - i}} - \mathop \leftharpoonup \limits_u } \right)}^2}} } , $

其中$ \mathop \leftharpoonup \limits_u =\frac{1}{m} \sum\limits_{i=1}^{m} u_{n-i}, u_{i}=\ln \frac{S_{i}}{S_{i-1}}, S_{i} $为第$ i $天末的收盘价. 由(6.1)式计算的$ \sigma _n $为股价的日波动率, 而定价模型(3.1)中的波动率$ \sigma $为股价的年波动率, 因此需通过下式

(6.2) $ \begin{equation} \sigma = \sigma _n \times \sqrt {252}, \end{equation} $

转变为年波动率, 计算可得万科股票价格的年波动率为$ \hat \sigma = {\rm{0}}{\rm{.4550934}} $.

运用$ {\rm{R/S}} $分析方法估计Hurst指数$ H $^[15], 对于股价序列$ x_1 , x_2 , \cdots , x_n $, 令$ X_n = \sum\limits_{k = 1}^n {x_k } $, 构造统计量

(6.3) $ \begin{equation} Q_n = \frac{{R_n }}{{S_n }}, \end{equation} $

其中$ R_n = \mathop {\max }\limits_{k \le n} \left( {X_k - \frac{k}{n}X_k } \right) - \mathop {\min }\limits_{k \le n} \left( {X_k - \frac{k}{n}X_k } \right), $$ S_n = \sqrt {\frac{1}{n}\sum\limits_{k = 1}^n {x_k^2 } - \left( {\frac{1}{n}\sum\limits_{k = 1}^n {x_k^2 } } \right)^2 }, $对于大的$ n $值, 统计量$ Q_n $可用$ cn^H $近似, 即

(6.4) $ \begin{equation} \frac{{R_n}}{{S_n}}\sim cn^H, \end{equation} $

其中$ c $为某个常数. 对(6.4)式两端取对数得$ \ln \left(R_{n} / S_{n}\right) \sim \ln c+H \ln n$因此对于股价数据得到相应的点列$ \left(\ln n, \ln \left(R_{n} / S_{n}\right)\right)$, 运用最小二乘法得到直线$ \hat a_n + \hat b_n \ln n $, 直线的斜率$ \hat b_n $即为Hurst指数$ H $的估计值. 由股票收盘价序列得Hurst指数的估计值为$ \hat H = {\rm{0}}{\rm{.5584205}} $.

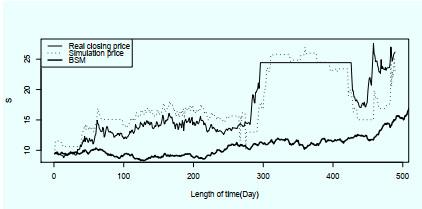
取万科2014年10月8日的收盘价9.44元作为初始值$ S_0 $, 其它各参数的取值分别为: $ H = 0.56 $, $ \alpha = 0.8 $, $ \sigma = 0.46 $, $ \mu = 0.05 $, 对于固定的时间步长$ \Delta {\rm{t}} $, 基于(3.1)式迭代得到股票价格的离散序列$ \left\{ {S_{t + i\Delta t} , {\kern 1pt} i = 1, 2, \cdots , n} \right\} $, 即得到股票价格的一条模拟路径, 并与真实股价以及经典的B-S定价模型所得到的模拟价进行对比, 如图 3所示.

由图$ 3 $以及表$ 3 $可知, 基于(3.1)式模拟的股票价格的标准差为4.55, 小于股价真实值的标准差5.44, 小于B-S定价模型得到的股价的标准差7.56, 并且模拟价与真实收盘价的走势较吻合, 因而本文采用的期权定价模型在刻画具有常值周期性特征的资产价格变动时是有效的.

通过假设标的资产(股票)价格变动服从时变混合分数布朗运动, 得到了在离散情形下带有交易成本的几何平均亚式看涨、看跌期权的定价公式. 基于数值试验, 对不同亚式期权定价公式得到的期权价格进行了比较, 发现本文所获得的定价公式更能体现出标的资产交易过程中产生的交易费用对期权价格的影响, 并且定价公式中的参数$ \alpha $、$ H $对于期权价格有明显的影响. 基于实证分析, 验证了定价模型(3.1)在刻画具有常值周期性特征的资产价格变动时具有有效性.