1 引言
考虑如下的抛物积分微分方程
其中
抛物积分微分方程来源于许多物理和工程实际问题,例如,具有记忆性质材料的热传导,粘弹性体压缩,流动流体核衰变等.积分项的出现使其与传统的抛物方程有着本质的区别,数值求解也更为困难.关于此类方程的有限元方法研究已经有了一些结果[1-16].文献[1-2]讨论了双线性元和类Wilson元的超收敛性.文献[3]得到了最佳的误差估计和解的正则性条件.文献[4]通过构造适当的插值后处理算子,得到了各向异性网格下的整体超收敛结果.文献[5]利用插值与投影相结合,在降低对解的光滑度要求下,得到了与以往文献相同的超逼近结果.文献[6-7]探讨了带弱奇异核的抛物积分微分方程的
本文中,
其中
2 单元的构造及性质
设
设
Wilson元的形函数空间为
其中
定义
其中
引理2.1 设
引理2.2 设
其中
引理2.3
3 半离散格式的收敛性分析
与(1.1)式等价的变分问题为:求
(3.1)式的传统半离散格式为:求
为提高逼近精度,我们引进新的半离散格式为:求
定理3.1 问题(3.3)存在唯一解.
证 设
在(3.3)式中选取
其中
从而(3.4)式是关于向量
下面先讨论上述问题的收敛性.
定理3.2 设
证 令
由于
根据(1.1)和(3.3)式有下面误差方程
在(3.5)式中令
首先注意到
下面对
将
对(3.8)式两边对变量
由于
将(3.10)和(3.11)式代入(3.9)式,则(3.9)式可化为
由文献[17]知(3.12)式左端可化为
从而当
应用Gronwall引理有
因此
证毕.
4 全离散逼近格式的收敛性分析
在本节中,将给出问题(3.1)的全离散逼近格式及相应的误差估计.将时间区间
建立(3.1)式的全离散逼近格式如下:求
定理4.1 设
证 记
其中,
在(4.2)式中令
首先注意到
其中
下面对
注意到(4.3)式左端
将
下面先估计上式最后一项,在(4.3)式中令
注意到
将(4.8)-(4.12)式代入(4.7)式,两边再同乘以
将(4.13)式代入(4.6)式得
注意到
将(4.15)–(4.18)式代入(4.14)式得
利用离散的Gronwall引理得
因此
证毕.
5 数值实验
在数值实验中,我们考虑如下抛物积分微分方程
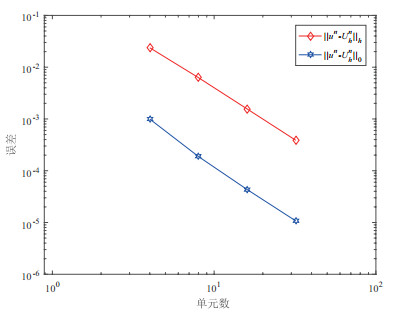
表 1
| 收敛阶 | 收敛阶 | |||
| 0.023734626 | --- | 0.000995509 | --- | |
| 0.006276340 | 1.9190 | 0.000187996 | 2.4047 | |
| 0.001559389 | 2.0089 | 0.000043305 | 2.1181 | |
| 0.000386405 | 2.0128 | 0.000010702 | 2.0167 |
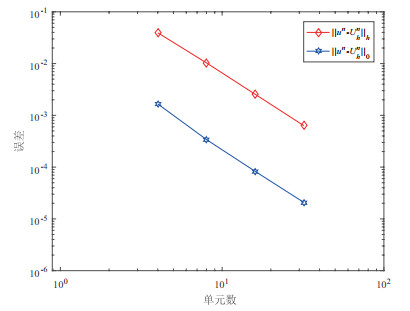
表 2
| 收敛阶 | 收敛阶 | |||
| 0.039374206 | --- | 0.001662729 | --- | |
| 0.010324365 | 1.9312 | 0.000341116 | 2.2852 | |
| 0.002554045 | 2.0152 | 0.000082887 | 2.0410 | |
| 0.000631856 | 2.0151 | 0.000020794 | 1.9950 |
图 1
图 2
6 结论
本文通过引入新的双线性型,对抛物积分微分方程分别构造了一种新的半离散格式和全离散格式,并且在比传统的能量模更大的范数意义下,得到了相应的比通常估计方法高一阶精度的收敛结果.在整个分析过程中,对(4.4)式的估计起到了关键作用.本文对其他偏微分方程的数值求解提供了可借鉴的思路和途径.
参考文献
抛物积分微分方程非协调类Wilson元的整体超收敛和外推
DOI:10.3969/j.issn.0255-7797.2013.02.013 [本文引用: 1]
Global superconvergence and extrapolation of quasi-wilson element solution to integro-differential of parabolic equations
DOI:10.3969/j.issn.0255-7797.2013.02.013 [本文引用: 1]
Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel
DOI:10.1090/S0025-5718-1992-1122059-2 [本文引用: 1]
抛物型积分微分方程各向异性非协调有限元分析
DOI:10.3969/j.issn.1005-3085.2009.02.003 [本文引用: 1]
Anisotropic nonconforming finite element analysis for integro-diferential equations of parabolic type
DOI:10.3969/j.issn.1005-3085.2009.02.003 [本文引用: 1]
抛物型积分微分方程双线性元方法的新估计
New error estimates of bilinear finite element method to parabolic type integro-differential equation
带弱奇异核的抛物型积分微分方程的非协调有限元方法
Noneonofrming finite element method for integro-diferential equation of parabolie type with weakly singular kernel
带弱奇异核非线性积分微分方程的有限元分析
DOI:10.3969/j.issn.1000-0984.2012.12.021 [本文引用: 1]
Finite element analysis of nonlinear integro differential equation with weakly singular kernel
DOI:10.3969/j.issn.1000-0984.2012.12.021 [本文引用: 1]
抛物型积分微分方程的非协调Wilson元方法
Nonconforming wilson element method for parabolic integro differential equations
非线性抛物积分微分方程的类Wilson非协调元分析
DOI:10.3969/j.issn.1001-9847.2012.04.032 [本文引用: 1]
Analysis of quasi-wilson nonconforming element for nonlinear parabolic integro-differential equation
DOI:10.3969/j.issn.1001-9847.2012.04.032 [本文引用: 1]
非线性抛物型积分微分方程非协调三角形Carey元的收敛性分析
Convergence analysis of the nonconforming triangular carey element for a kind of nonlinear parabolic integro-differential problems
抛物型积分-微分方程有限元近似的超收敛性质
DOI:10.3969/j.issn.1000-081X.2001.03.001 [本文引用: 1]
Superconvergence of finite element approximations to integro-differential equations of parabolic type
DOI:10.3969/j.issn.1000-081X.2001.03.001 [本文引用: 1]
An H1-Galerkin nonconforming mixed finite element method for integro-differential equation of parabolic type
抛物型积分微分方程新混合元格式的超逼近分析
Superclose analysis of a new mixed finite element scheme for parabolic intergro-differential equations
拟线性抛物型积分微分方程的一个新最低阶混合元格式
DOI:10.3969/j.issn.1000-0984.2012.23.037
A new lowest order nonconforming mixed finite element formulation for quasi-linear integro-differential equation of parabolic type
DOI:10.3969/j.issn.1000-0984.2012.23.037
抛物型积分微分方程的一个新低阶混合元格式
DOI:10.3969/j.issn.1000-2162.2012.06.001
A new low order nonconforming mixed finite element formulation for integro-differential equations of parabolic type
DOI:10.3969/j.issn.1000-2162.2012.06.001
伪抛物型积分微分方程一个新的混合有限元分析
A new mixed finite element analysis for pseudo-parabolic intergo-differential equation
A nonconforming scheme to solve the parabolic problem
DOI:10.1016/j.amc.2015.04.089 [本文引用: 6]
Wilson元求解二阶椭圆问题的一种新格式
A new scheme of wilson element for second-order elliptic problems
Interior penalty procedures for elliptic and parabolic galerkin methods
H(div)-conforming finite elements for the brinkman problem
DOI:10.1142/S0218202511005726 [本文引用: 1]