数学物理学报 ›› 2023, Vol. 43 ›› Issue (3): 957-969.
基于Ornstein-Uhlenbeck过程下具有两个再保险公司的比例再保险与投资
- 1福建师范大学数学与统计学院 福州350117
2福建省分析数学及应用重点实验室 福州350117
-
收稿日期:2022-04-25修回日期:2023-02-06出版日期:2023-06-26发布日期:2023-06-01 -
通讯作者:陈密 E-mail:hl2193088930@163.com;chenmi0610@163.com -
作者简介:黄玲,E-mail:hl2193088930@163.com -
基金资助:国家自然科学基金(11701087);福建省自然科学基金(2019J01673)
Proportional Reinsurance and Investment Based on the Ornstein-Uhlenbeck Process in the Presence of Two Reinsurers
Huang ##1( ),Liu Haiyan1,2,Chen Mi1,2,*(
),Liu Haiyan1,2,Chen Mi1,2,*( )
)
- 1School of Mathematics and Statistics, Fujian Normal University, Fuzhou 350117
2Fujian Provincial Key Laboratory of Mathematical Analysis and its Applications, Fuzhou 350117
-
Received:2022-04-25Revised:2023-02-06Online:2023-06-26Published:2023-06-01 -
Contact:Mi Chen E-mail:hl2193088930@163.com;chenmi0610@163.com -
Supported by:NSFC(11701087);NSF of Fujian Province(2019J01673)
摘要:
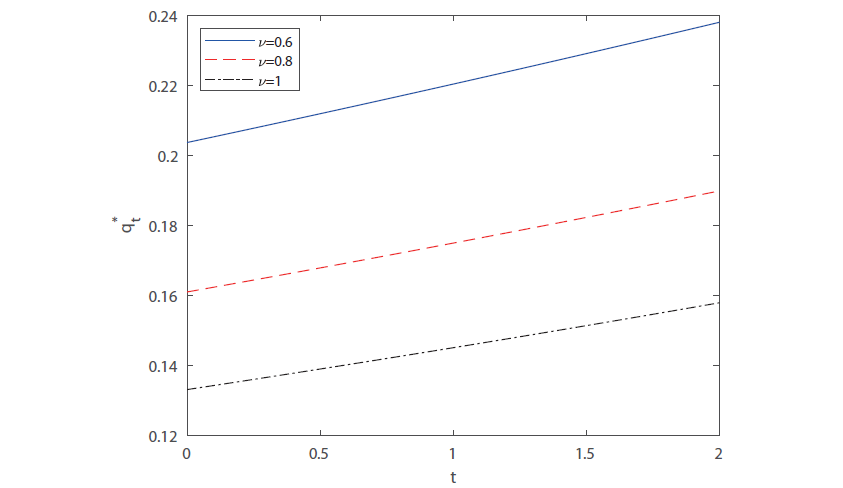
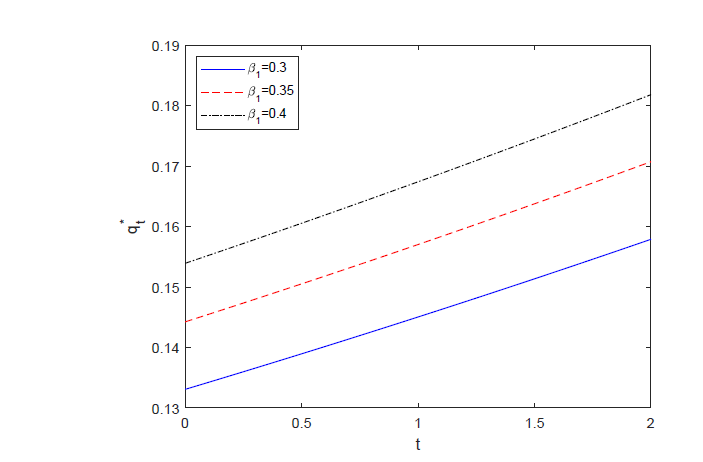
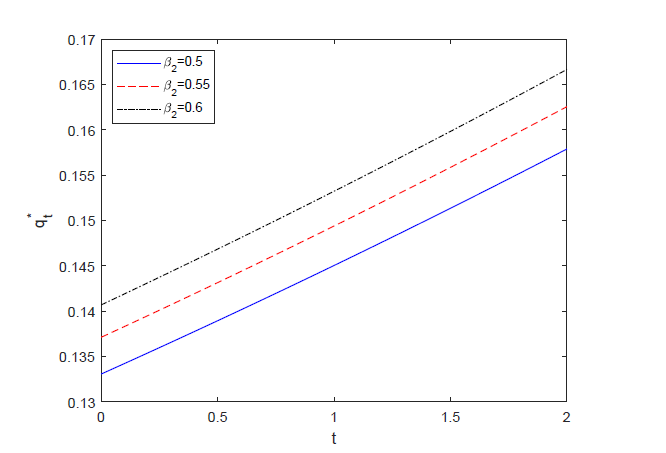
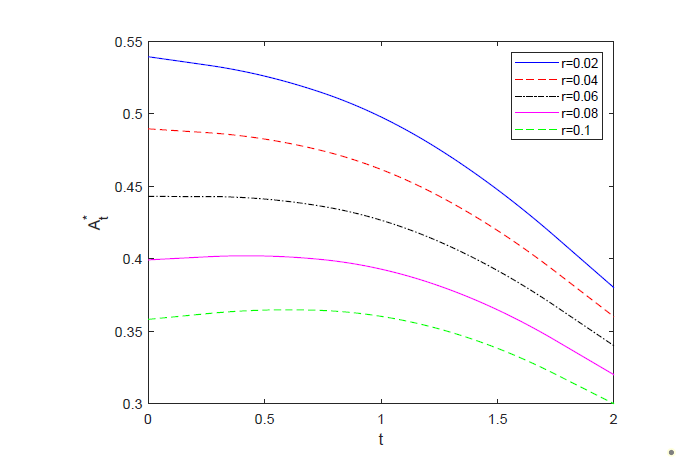
该文研究了两类风险模型下具有两个再保险公司的最优再保险和投资问题.保险公司购买比例再保险并投资于无风险资产和风险资产组成的金融市场,其风险资产价格模型受Ornstein-Uhlenbeck过程影响.假设再保险的保费按照指数保费原则来计算,保险公司的目标是使终端财富的期望指数效用最大化.利用随机控制理论和HJB方程,推导出了最优策略和值函数的显式表达式.最后,通过数值分析验证了模型参数对最优策略的影响.
中图分类号:
- O211.6
引用本文
黄玲,刘海燕,陈密. 基于Ornstein-Uhlenbeck过程下具有两个再保险公司的比例再保险与投资[J]. 数学物理学报, 2023, 43(3): 957-969.
Huang ,Liu Haiyan,Chen Mi. Proportional Reinsurance and Investment Based on the Ornstein-Uhlenbeck Process in the Presence of Two Reinsurers[J]. Acta mathematica scientia,Series A, 2023, 43(3): 957-969.
使用本文
| [1] |
Browne S. Optimal investment policies for a firm with random risk process: exponential utility and minimizing the probability of ruin. Mathematics of Operations Research, 1995, 20(4): 937-958
doi: 10.1287/moor.20.4.937 |
| [2] |
Liu C S, Yang H L. Optimal investment for an insurer to minimize its probability of ruin. North American Actuarial Journal, 2004, 8(2): 11-31
doi: 10.1080/10920277.2004.10596134 |
| [3] | Liang Z B. Optimal proportional reinsurance for controlled risk process which is perturbed by diffusion. Acta Mathematicae Applicatae Sinica (English Series), 2007, 23(3): 477-488 |
| [4] |
Chen M, Peng X F, Guo J Y. Optimal dividend problem with a nonlinear regular-singular stochastic control. Insurance: Mathematics and Economics, 2013, 52(3): 448-456
doi: 10.1016/j.insmatheco.2013.02.010 |
| [5] | Meng Q B, Li Z D, Wang M H, Zhang X. Stochastic optimal control models for the insurance company with bankruptcy return. Applied Mathematics and Information Sciences, 2013, 7(1L): 273-282 |
| [6] |
Li D P, Rong X M, Zhao H. Time-consistent reinsurance-investment strategy for an insurer and a reinsurer with mean-variance criterion under the CEV model. Journal of Computational and Applied Mathematics, 2015, 283: 142-162
doi: 10.1016/j.cam.2015.01.038 |
| [7] |
Xu L, Zhang L M, Yao D J. Optimal investment and reinsurance for an insurer under Markov-modulated financial market. Insurance: Mathematics and Economics, 2017, 74: 7-19
doi: 10.1016/j.insmatheco.2017.02.005 |
| [8] |
Wang Y J, Rong X M, Zhao H. Optimal investment strategies for an insurer and a reinsurer with a jump diffusion risk process under the CEV model. Journal of Computational and Applied Mathematics, 2018, 328: 414-431
doi: 10.1016/j.cam.2017.08.001 |
| [9] |
Bi J N, Cai J. Optimal investment-reinsurance strategies with state dependent risk aversion and VaR constraints in correlated markets. Insurance: Mathematics and Economics, 2019, 85: 1-14
doi: 10.1016/j.insmatheco.2018.11.007 |
| [10] |
Chen M, Yuen K C, Wang W Y. Optimal reinsurance and dividends with transaction costs and taxes under thinning structure. Scandinavian Actuarial Journal, 2021, 2021(3): 198-217
doi: 10.1080/03461238.2020.1824158 |
| [11] |
Zhou Z B, Bai Y F, Xiao H L, Chen X. A non-zero-sum reinsurance-investment game with delay and asymmetric information. Journal of Industrial and Management Optimization, 2021, 17(2): 909-936
doi: 10.3934/jimo.2020004 |
| [12] |
Li N, Wang W. Optimal dividend and proportional reinsurance strategy under standard deviation premium principle. Bulletin of the Malaysian Mathematical Sciences Society, 2022, 45(2): 869-888
doi: 10.1007/s40840-021-01220-w |
| [13] |
Young V R, Zariphopoulou T. Pricing dynamic insurance risks using the principle of equivalent utility. Scandinavian Actuarial Journal, 2002, 2002(4): 246-279
doi: 10.1080/03461230110106327 |
| [14] |
Young V R. Equity-indexed life insurance: pricing and reserving using the principle of equivalent utility. North American Actuarial Journal, 2003, 7(1): 68-86
doi: 10.1080/10920277.2003.10596078 |
| [15] |
Moore K S, Young V R. Pricing equity-linked pure endowments via the principle of equivalent utility. Insurance: Mathematics and Economics, 2003, 33(3): 497-516
doi: 10.1016/S0167-6687(03)00166-5 |
| [16] |
Musiela M, Zariphopoulou T. An example of indifference prices under exponential preferences. Finance and Stochastics, 2004, 8(2): 229-239
doi: 10.1007/s00780-003-0112-5 |
| [17] |
Chen T, Liu W, Tan T, et al. Optimal reinsurance with default risk: a reinsurer's perspective. Journal of Industrial and Management Optimization, 2021, 17(5): 2971-2987
doi: 10.3934/jimo.2020103 |
| [18] |
Liang Z B, Yuen K C. Optimal dynamic reinsurance with dependent risks: variance premium principle. Scandinavian Actuarial Journal, 2016, 2016(1): 18-36
doi: 10.1080/03461238.2014.892899 |
| [19] |
Han X, Liang Z B, Young V R. Optimal reinsurance to minimize the probability of drawdown under the mean-variance premium principle. Scandinavian Actuarial Journal, 2020, 2020(10): 879-903
doi: 10.1080/03461238.2020.1788136 |
| [20] |
Wen C. Pricing catastrophe reinsurance under the standard deviation premium principle. AIMS Mathematics, 2022, 7(3): 4472-4484
doi: 10.3934/math.2022249 |
| [21] |
Chi Y C, Meng H. Optimal reinsurance arrangements in the presence of two reinsurers. Scandinavian Actuarial Journal, 2014, 2014(5): 424-438
doi: 10.1080/03461238.2012.723638 |
| [22] |
Chen M, Yuen K C. Optimal dividend and reinsurance in the presence of two reinsurers. Journal of Applied Probability, 2016, 53(2): 554-571
doi: 10.1017/jpr.2016.20 |
| [23] |
Meng H, Zhou M, Siu T K. Optimal reinsurance policies with two reinsurers in continuous time. Economic Modelling, 2016, 59(1): 182-195
doi: 10.1016/j.econmod.2016.07.009 |
| [24] |
Yao D J, Fan K. Optimal risk control and dividend strategies in the presence of two reinsurers: Variance premium principle. Journal of Industrial and Management Optimization, 2017, 14(3): 1055-1083
doi: 10.3934/jimo.2017090 |
| [25] | Baev A V, Bondarev B V. On the ruin probability of an insurance company dealing in a BS-market. Theory of Probability and Mathematical Statistics, 2007, 74: 11-23 |
| [26] |
Liang Z B, Yuen K C, Guo J Y. Optimal proportional reinsurance and investment in a stock market with Ornstein-Uhlenbeck process. Insurance: Mathematics and Economics, 2011, 49: 207-215
doi: 10.1016/j.insmatheco.2011.04.005 |
| [27] |
Tian Y X, Guo J Y, Sun Z Y. Optimal mean-variance reinsurance in a financial market with stochastic rate of return. Journal of Industrial and Management Optimization, 2021, 17(4): 1887-1912
doi: 10.3934/jimo.2020051 |
| [28] |
Li Y, Mao X R, Song Y Z, Tao J. Optimal investment and proportional reinsurance strategy under the mean-reverting Ornstein-Uhlenbeck process and net profit condition. Journal of Industrial and Management Optimization, 2022, 18(1): 75-93
doi: 10.3934/jimo.2020143 |
| [29] |
A C X, Gu A L, Shao Y. Optimal reinsurance and investment strategy with delay in Heston's SV model. Journal of the Operations Research Society of China, 2021, 9(2): 245-271
doi: 10.1007/s40305-020-00331-8 |
| [30] |
Bai Y F, Zhou Z B, Xiao H L, et al. A hybrid stochastic differential reinsurance and investment game with bounded memory. European Journal of Operational Research, 2021, 296(2): 717-737
doi: 10.1016/j.ejor.2021.04.046 |
| [31] |
Liu S S, Guo W J, Tong X L. Martingale method for optimal investment and proportional reinsurance. Applied Mathematics: A Journal of Chinese Universities, 2021, 36(1): 16-30
doi: 10.1007/s11766-021-3463-8 |
| [32] |
Yang H, Zhang L. Optimal investment for insurer with jump-diffusion risk process. Insurance: Mathematics and Economics, 2005, 37: 615-634
doi: 10.1016/j.insmatheco.2005.06.009 |
| [1] | 卢嘉鑫,董华. 基于4/2随机波动率模型考虑错误定价和保费退还条款的DC型养老金计划的均衡投资策略[J]. 数学物理学报, 2023, 43(3): 939-956. |
| [2] | 季锟鹏,彭幸春. 考虑通胀风险与最低绩效保障的损失厌恶型保险公司的最优投资与再保险策略[J]. 数学物理学报, 2022, 42(4): 1265-1280. |
| [3] | 陈旭. Lévy模型下的最优寿险、消费和投资[J]. 数学物理学报, 2022, 42(1): 306-320. |
| [4] | 赵玉莹,温玉珍. 模糊厌恶下最小Drawdown概率的最优投资再保险策略[J]. 数学物理学报, 2021, 41(4): 1147-1165. |
| [5] | 陈密, 郭军义. 指数保费准则下的最优投资和比例再保险[J]. 数学物理学报, 2014, 34(5): 1161-1172. |
| [6] | 张昕丽, 孙文瑜. 考虑交易费用和债务的再保险和投资问题[J]. 数学物理学报, 2012, 32(1): 137-147. |
| [7] | 王春伟, 尹传存. 具有投资利息的扰动复合Poisson风险模型的最优分红策略[J]. 数学物理学报, 2011, 31(6): 1567-1578. |
| [8] | 毕俊娜, 郭军义. 均值-方差准则下的投资连结寿险合同对冲问题[J]. 数学物理学报, 2011, 31(5): 1141-1149. |
| [9] | 李育强. 带移民Jirina过程的弱极限定理[J]. 数学物理学报, 2009, 29(2): 303-315. |
| [10] | 薛明皋; 龚朴. 非对称情形下R & D竞争项目的策略性投资[J]. 数学物理学报, 2008, 28(5): 794-801. |
| [11] | 彭大衡;. 具有分数O-U过程的永久美式看跌期权的定价[J]. 数学物理学报, 2007, 27(6): 1141-1147. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 270
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 106
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|