大规模三模网络自回归模型

摘要/Abstract

图/表 9

参考文献 26

Metrics

摘要：

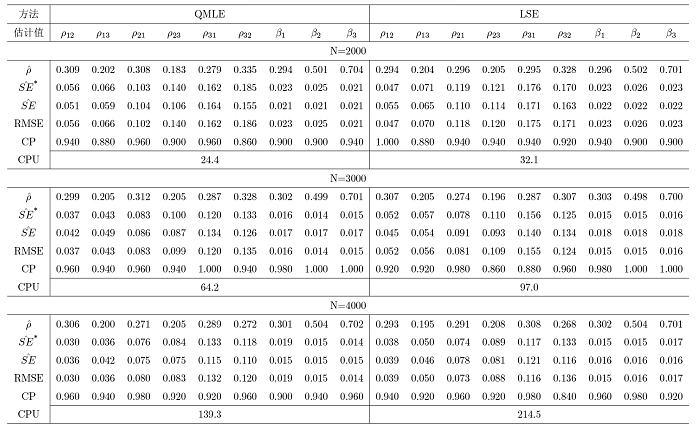
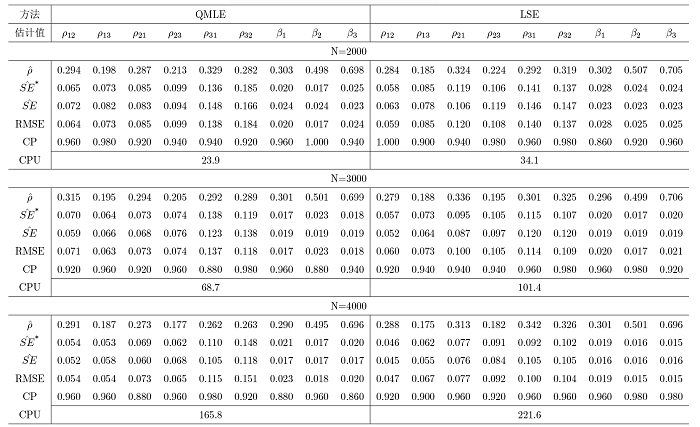
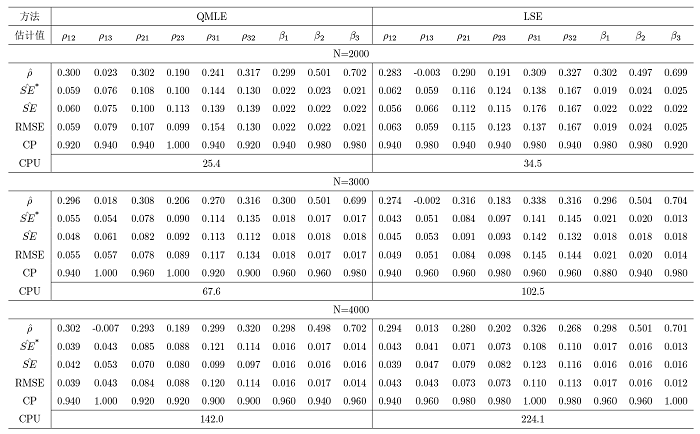
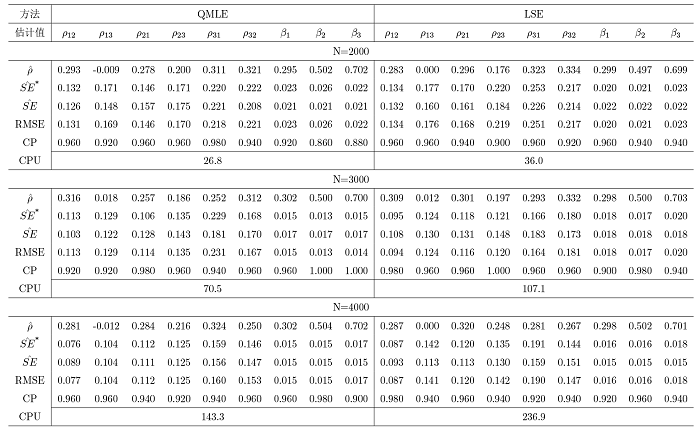
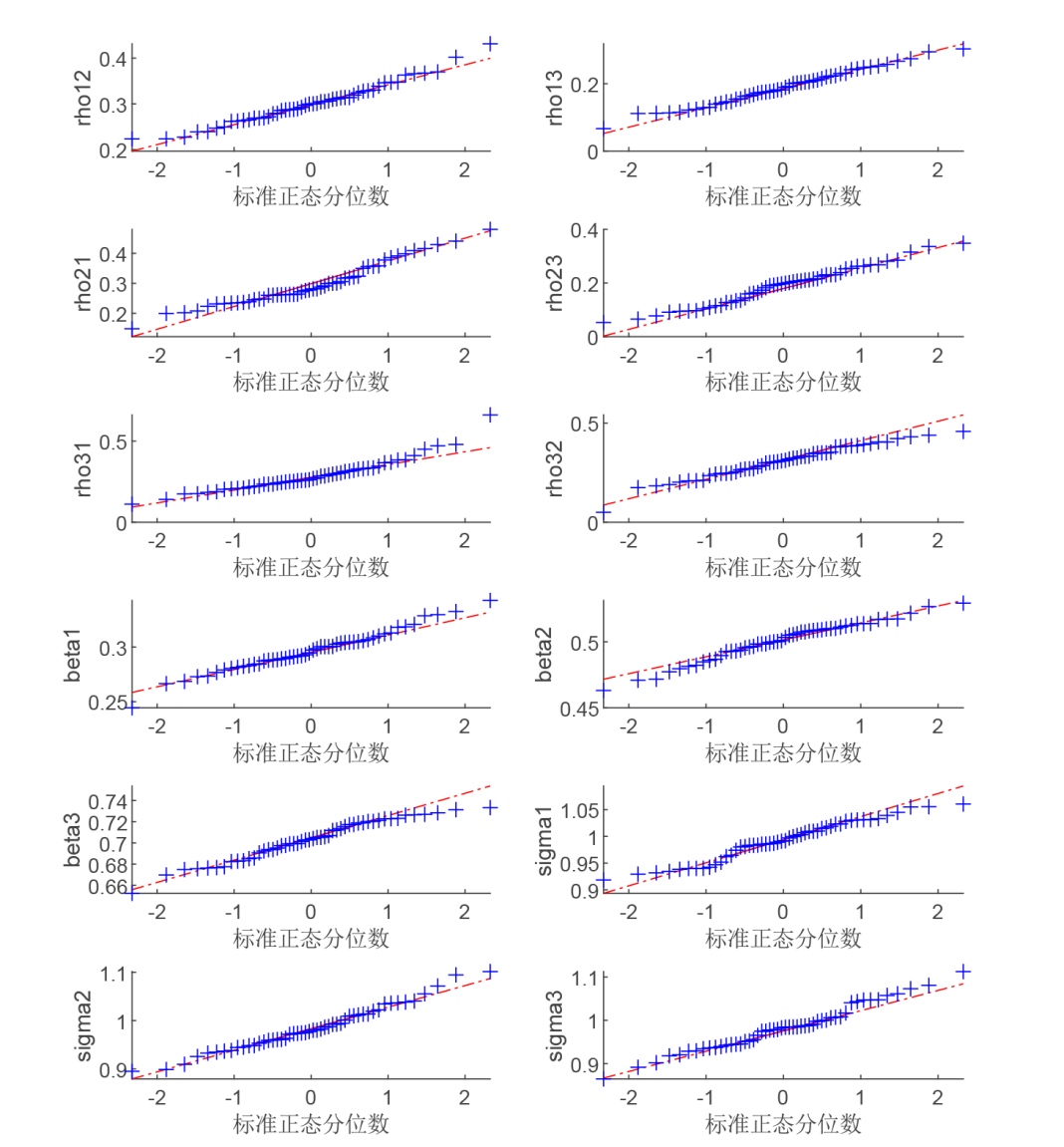
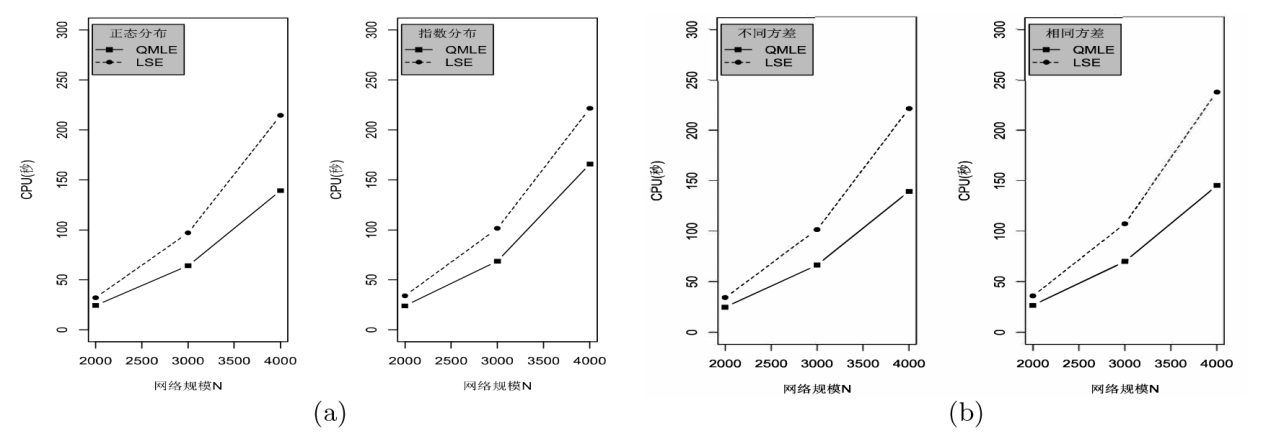
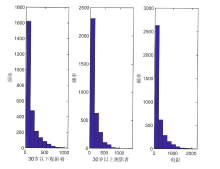
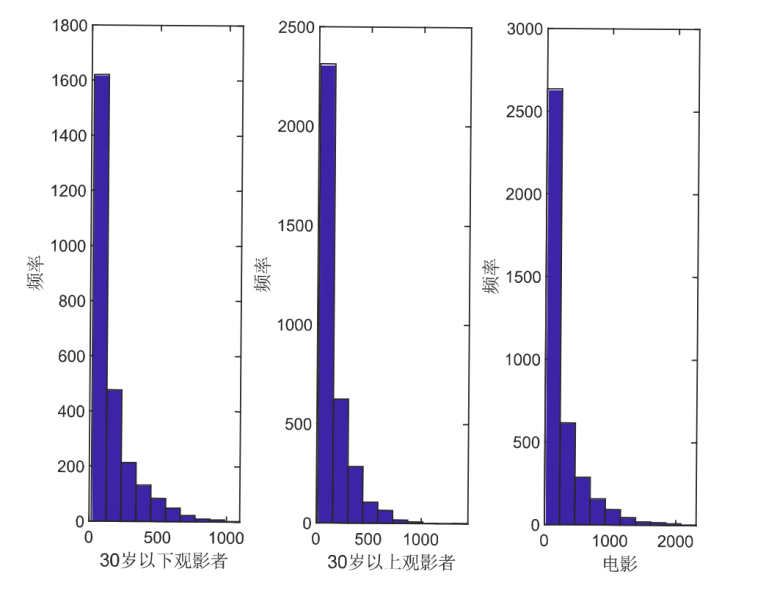
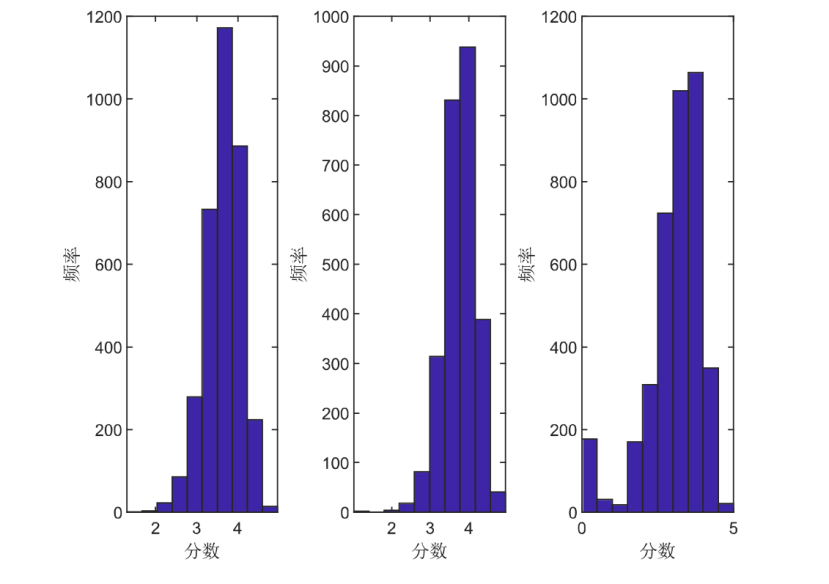
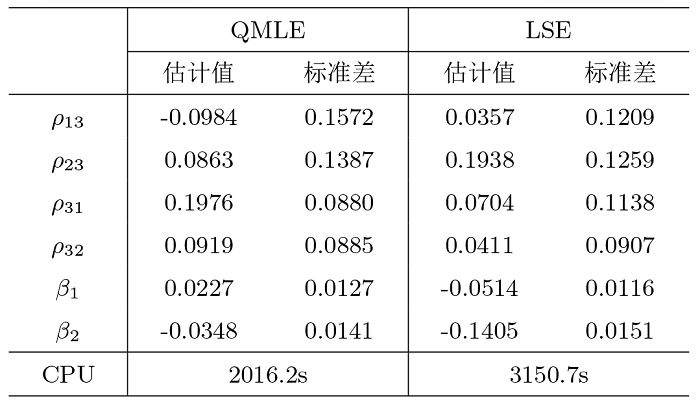
在双模网络自回归 (NAR) 模型的基础上给出了三模 NAR 模型. 该模型考虑了大规模社交网络中三种类型的节点, 且边只允许出现在不同类型的节点之间. 首先介绍了模型的定义以及模型的可逆性与参数可识别性, 考虑了拟极大似然和条件最小二乘估计方法及相应估计量的大样本性质. 其次, 在多种设定下进行了数值模拟, 对估计方法的准确性与计算效率进行了对比, 最后分析了一个实际例子.

关键词: 三模 NAR 模型, 拟极大似然, 条件最小二乘, 大样本性质

Abstract:

Based on the two-mode network autoregressive (NAR) model, the specific form of the three-mode NAR model is given. This model considers three types of nodes in large-scale social networks, and edges are only allowed to occur between different types of nodes. First, the definition of the model, the reversibility and parameter identification of the model are introduced, and the estimation methods of quasi-maximum likelihood and conditional least squares and the large sample properties of the corresponding estimators are considered. Second, numerical simulations are carried out in multiple cases, the accuracy of the estimation methods and computational efficiency are compared, and finally a practical example is analyzed.

Key words: Three-mode NAR model, Quasi-maximum likelihood, Conditional least squares, Large-sample properties

中图分类号:

O212

卫奕冰, 朱复康. 大规模三模网络自回归模型[J]. 数学物理学报, 2024, 44(3): 783-803.

Wei Yibing, Zhu Fukang. Autoregressive Model for Large-scale Three-mode Networks[J]. Acta mathematica scientia,Series A, 2024, 44(3): 783-803.

表1

表2

表3

表4

图1

表1 中 $N=4000$ 时 QMLE 估计量的 QQ 图"

图1

图2

图3

图4

表5

[1]	Anselin L. Spatial Econometrics:Methods and Models. New York: Springer, 1988
[2]	Borgatti S P, Everett M G. Network analysis of 2-mode data. Social Networks, 1997, 19: 243-269
[3]	Cai Q, Liu J M. Hierarchical clustering of bipartite networks based on multiobjective optimization. IEEE Transactions on Network Science and Engineering, 2020, 7: 421-434
[4]	Chen E, Fan J, Zhu X. Community network auto-regression for high-dimensional time serie. Journal of Econometrics, 2023, 235: 1239-1256
[5]	Chen X, Chen Y, Xiao P. The impact of sampling and network topology on the estimation of social intercorrelations. Journal of Marketing Research, 2013, 50: 95-110
[6]	Cohen-Cole E, Liu X, Zenou Y. Multivariate choices and identification of social interactions. Journal of Applied Econometrics, 2018, 33: 165-178
[7]	D'Esposito M R, De Stefano D, Ragozini G. On the use of multiple correspondence analysis to visually explore affiliation networks. Social Networks, 2014, 38: 28-40
[8]	Everett M G, Borgatti S P. The dual-projection approach for two-mode networks. Social Networks, 2013, 35: 204-210
[9]	Feng L, Zhou C, Zhao Q. A spectral method to find communities in bipartite networks. Physica A, 2019, 513: 424-437 doi: 10.1016/j.physa.2018.09.022
[10]	Gao M, Chen L. A projection based algorithm for link prediction in bipartite network. International Conference on Information System and Artifical Intelligence, 2016: 56-61
[11]	Huang D. Least squares estimation of spatial autoregressive models for large-scale social networks. Electronic Journal of Statistics, 2019, 13: 1135-1165
[12]	Huang D, Wang F, Zhu X, Wang H. Two-mode network autoregressive model for large-scale networks. Journal of Econometrics, 2020, 216: 203-219
[13]	Kelejian H H, Prucha I R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. Journal of Econometrics, 2010, 157: 53-67 pmid: 20577573
[14]	Lee L. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica, 2004, 72: 1899-1925
[15]	LeSage J P, Pace R K. Introduction to Spatial Econometrics. Boca Raton: Chapman and Hall/CRC, 2009
[16]	Li X, Chen H. Recommendation as link prediction in bipartite graphs: A graph kernel-based machine learning approach. Decision Support Systems, 2013, 54: 880-890
[17]	Liu X. Identification and efficient estimation of simultaneous equations network models. Journal of Business & Econometrics Statistics, 2014, 32: 516-536
[18]	Malikov E, Sun Y. Semiparametric estimation and testing of smooth coefficient spatial autoregressive models. Journal of Econometrics, 2017, 199: 12-34
[19]	Ord K. Estimation methods for models of spatial interaction. Journal of the American Statistical Association, 1975, 70: 120-126
[20]	Ouyang F. Using three social network analysis approaches to understand computer-supported collaborative learning. Journal of Educational Computing Research, 2021, 59: 1401-1424
[21]	Seber G A. A Matrix Handbook for Statisticians. New York: Wiley, 2008
[22]	Shumway R, Stoffer D. Time Series Analysis and Its Applications. New York: Springer, 2017
[23]	White H. Estimation, Inference and Specification Analysis. Cambridge: Cambridge University Press, 1996
[24]	Yang K, Lee L F. Identification and QML estimation of multivariate and simultaneous equations spatial autoregressive models. Journal of Econometrics, 2017, 196: 196-214
[25]	Zhu X, Pan R. Grouped network vector autoregression. Statistica Sinica, 2020, 30: 1437-1462.
[26]	Zhu X, Pan R, Li G, et al. Network vector autoregression. Annals of Satistics, 2017, 45: 1096-1123

Just accepted

Online first

Just accepted

Online first

Viewed

Full text

	From	local

	Times	89
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	63

From	Others	local

Times	57	6
Rate	90%	10%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed