一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型

数学物理学报 ›› 2024, Vol. 44 ›› Issue (3): 771-782.

一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型

徐瑞^1,^2,^*(),周凯娟^1,^2,³,白宁^1,^2,³

1.山西大学复杂系统研究所太原 030006
2.山西省疾病防控的数学技术与大数据分析重点实验室太原 030006
3.山西大学数学科学学院太原 030006

收稿日期:2022-10-26 修回日期:2023-11-01 出版日期:2024-06-26 发布日期:2024-05-17
通讯作者: *徐瑞，E-mail:rxu88@163.com;xurui@sxu.edu.cn
基金资助:
国家自然科学基金(12271317);国家自然科学基金(11871316)

A with-in Host HIV-1 Infection Dynamics Model Based on Virus-to-cell Infection and Cell-to-cell Transmission

Xu Rui^1,^2,^*(),Zhou Kaijuan^1,^2,³,Bai Ning^1,^2,³

1. Complex Systems Research Center, Shanxi University, Taiyuan 030006
2. Shanxi Key Laboratory of Mathematical Techniques and Big Data Analysis on Disease Control and Prevention, Shanxi University, Taiyuan 030006
3. School of Mathematics Science, Shanxi University, Taiyuan 030006

Received:2022-10-26 Revised:2023-11-01 Online:2024-06-26 Published:2024-05-17
Supported by:
NSFC(12271317);NSFC(11871316)

摘要/Abstract

摘要：

该文考虑一类具有细胞-细胞传播、胞内时滞、饱和 CTL 免疫反应和免疫损害的 HIV-1 感染动力学模型. 通过计算得到了免疫未激活和免疫激活再生率. 通过分析特征方程根的分布, 讨论了可行平衡点的局部渐近稳定性. 通过构造适当的 Lyapunov 泛函并应用 LaSalle 不变性原理, 证明了模型的全局动力学由免疫未激活和免疫激活再生率决定: 如果免疫未激活再生率小于 1, 则病毒未感染平衡点是全局渐近稳定的; 如果免疫未激活再生率大于 1 且免疫激活再生率小于 1, 则免疫未激活感染平衡点是全局渐近稳定的; 如果免疫激活再生率大于 1, 则慢性感染平衡点是全局渐近稳定的. 此外, 通过数值模拟说明了免疫损害和细胞-细胞传播对模型动力学的影响.

关键词: HIV-1 感染, 细胞-细胞传播, 胞内时滞, 饱和 CTL 免疫反应, 免疫损害, 稳定性

Abstract:

In this paper, we consider an HIV-1 infection model with cell-to-cell transmission, intracellular delay, saturated CTL immune response and immune impairment. By calculation, we get immunity-inactivated and immunity-activated reproduction ratios. By analyzing the characteristic equations, the local stability of each of feasible equilibria is established. By means of suitable Lyapunov functional and LaSalle's invariance principle, it is proved that the global asymptotic stability of each of feasible equilibria is determined by immunity-inactivated and immunity-activated reproduction ratios: If the immunity-inactivated reproduction ratio is less than unity, the infection-free equilibrium is globally asymptotically stable; if the immunity-inactivated reproduction ratio is greater than unity and the immunity-activated reproduction ratio is less than unity, the immunity-inactivated infection equilibrium is globally asymptotically stable; if the immunity-activated reproduction ratio is greater than unity, the chronic infection equilibrium is globally asymptotically stable. In addition, numerical simulation is carried out to illustrate the effects of immune impairment and cell-to-cell transmission on dynamics of the model.

Key words: HIV-1 infection, Cell-to-cell transmission, Intracellular delay, Saturated CTL immune response, Immune impairment, Stability

中图分类号:

O175.23

徐瑞, 周凯娟, 白宁. 一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型[J]. 数学物理学报, 2024, 44(3): 771-782.

Xu Rui, Zhou Kaijuan, Bai Ning. A with-in Host HIV-1 Infection Dynamics Model Based on Virus-to-cell Infection and Cell-to-cell Transmission[J]. Acta mathematica scientia,Series A, 2024, 44(3): 771-782.

图/表 5

参考文献 24

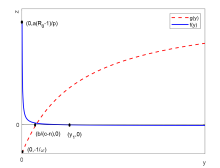
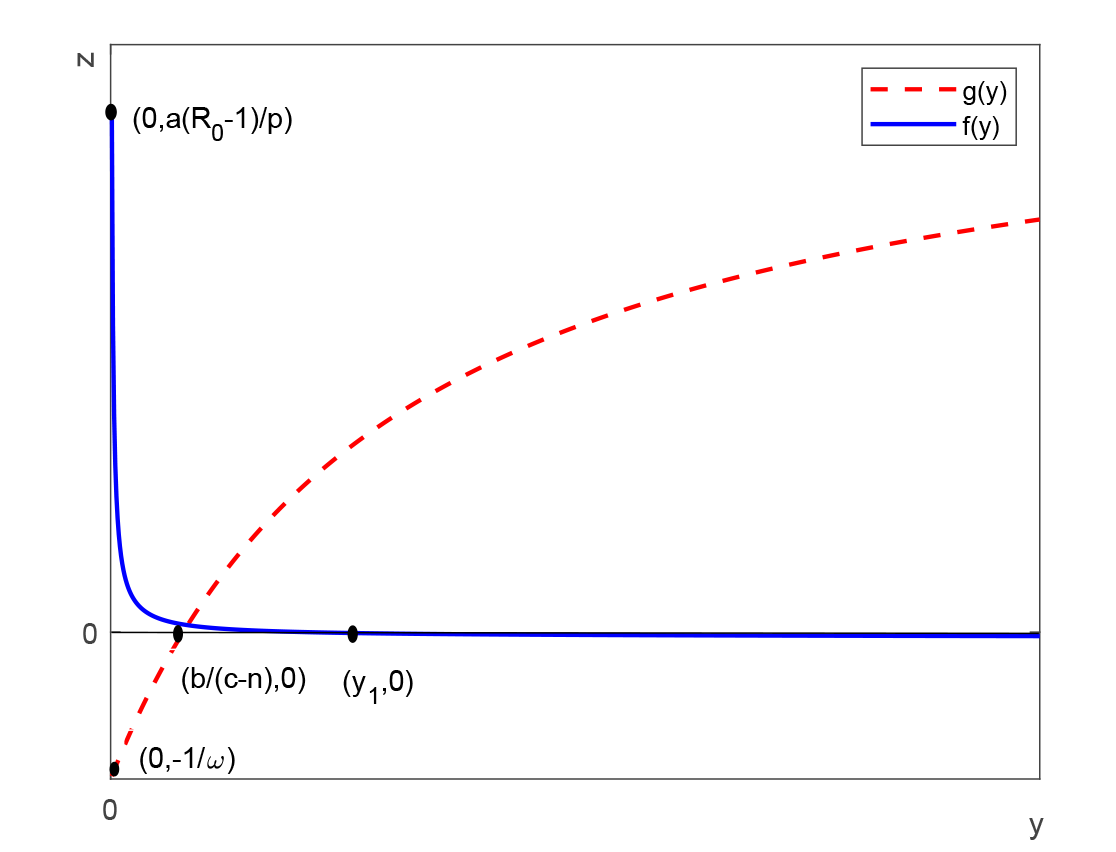
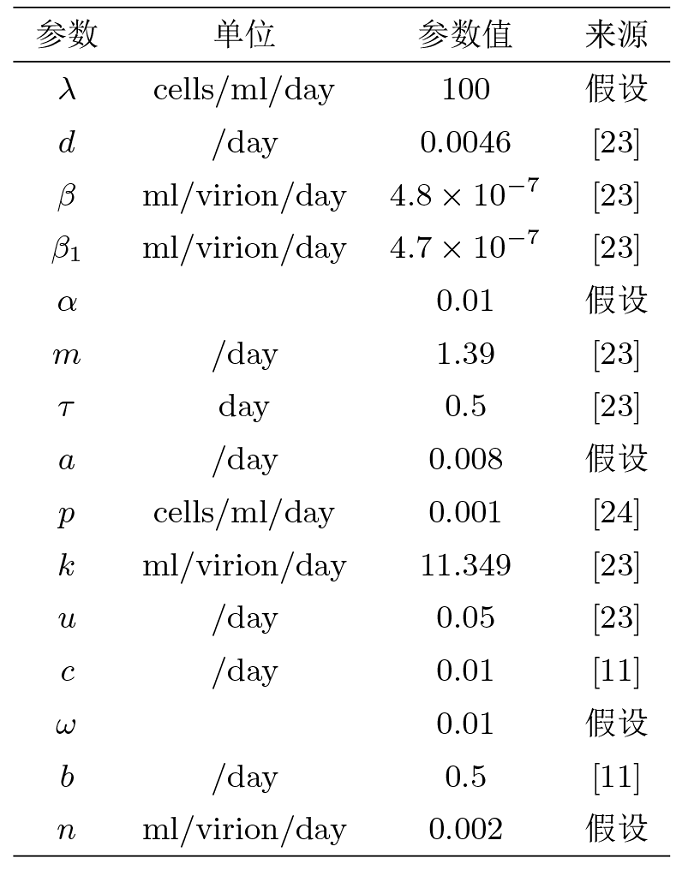
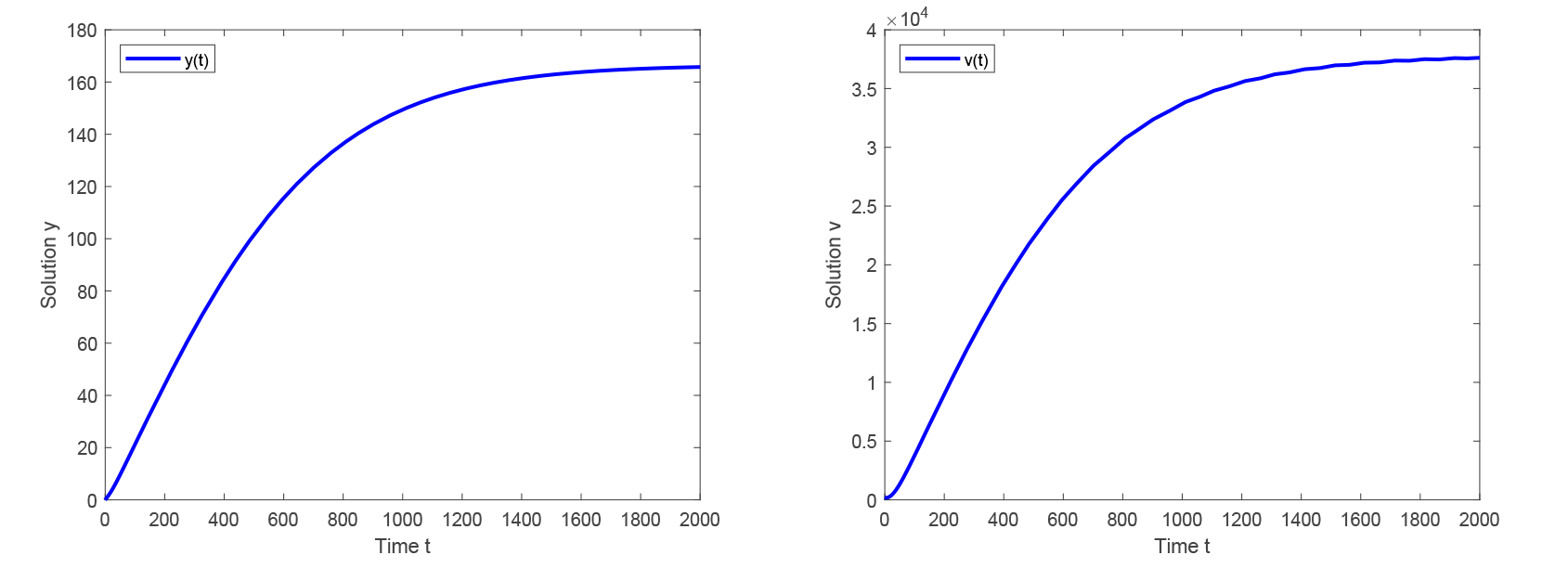
[1]	Perelson A S, Neumann A U, Markowitz M, et al. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life-span, and viral generation time. Science, 1996, 271(5255): 1582-1586 pmid: 8599114
[2]	Egger M, Hirschel B, Francioli P, et al. Impact of new antiretroviral combination therapies in HIV infected patients in Switzerland: Prospective multicentre study. The British Medical Journal, 1997, 315(7117): 1194-1199
[3]	Perelson A S, Nelson P W. Mathematical analysis of HIV-1: Dynamics in vivo. SIAM Review, 1999, 41(1): 3-44
[4]	Wasserstein-Robbins F. A mathematical model of HIV infection: Simulating T4, T8, macrophages, antibody, and virus via specific anti-HIV response in the presence of adaptation and tropism. Bulletin of Mathematical Biology, 2010, 72(5): 1208-1253 doi: 10.1007/s11538-009-9488-5 pmid: 20151219
[5]	Weusten J, Drimmelen H, Lelie P N. Mathematic modeling of the risk of HBV, HCV, and HIV transmission by window phase donations not detected by NAT. Transfusion, 2010, 42(5): 537-548
[6]	Yan Y, Wang W. Global stability of a five-dimensional model with immune responses and delay. Discrete and Continuous Dynamical Systems-B, 2011, 17(1): 401-416
[7]	Jiang C, Wang W. Complete classification of global dynamics of a virus model with immune response. Discrete and Continuous Dynamical Systems-B, 2014, 19(4): 1087-1103
[8]	Willie R, Zheng P, Parumasur N, et al. Asymptotic and stability dynamics of an HIV-1-Cytotoxic T Lymphocytes (CTL) chemotaxis model. Journal of Nonlinear Science, 2020, 30(3): 1055-1080
[9]	Wang Y, Zhou Y C, Brauer F, et al. Viral dynamics model with CTL immune response incorporating antiretroviral therapy. Journal of Mathematical Biology, 2013, 67(4): 901-934 doi: 10.1007/s00285-012-0580-3 pmid: 22930342
[10]	Kang C J, Miao H, Chen X, et al. Global stability of a diffusive and delayed virus dynamics model with Crowley-Martin incidence function and CTL immune response. Advances in Difference Equations, 2017, 2017(1): 1-16
[11]	Ren J, Xu R, Li L C. Global stability of an HIV infection model with saturated CTL immune response and intracellular delay. Mathematical Biosciences and Engineering, 2021, 18(1): 57-68
[12]	Sattentau Q. Avoiding the void: Cell-to-cell spread of human viruses. Nature Reviews Microbiology, 2008, 6(11): 815-826 doi: 10.1038/nrmicro1972 pmid: 18923409
[13]	Sattentau Q. The direct passage of animal viruses between cells. Current Opinion in Virology, 2011, 1(5): 396-402 doi: 10.1016/j.coviro.2011.09.004 pmid: 22440841
[14]	Gummuluru S, Kinsey C M, Emerman M. An in vitro rapid-turnover assay for human immunodeficiency virus type 1 replication selects for cell-to-cell spread of virus. Journal of Virology, 2000, 74(23): 10882-10891 pmid: 11069982
[15]	Lai X L, Zou X F. Modeling cell-to-cell spread of HIV-1 with logistic target cell growth. Journal of Mathematical Analysis and Applications, 2015, 426(1): 563-584
[16]	Pourbashash H, Pilyugin S S, Leenheer P D, et al. Global analysis of within host virus models with cell-to-cell viral transmission. Discrete and Continuous Dynamical Systems, 2014, 19(10): 3341-3357
[17]	Akbari N, Asheghi R. Optimal control of an HIV infection model with logistic growth, celluar and homural immune response, cure rate and cell-to-cell spread. Boundary Value Problems, 2022, Article number 5
[18]	Iwami S, Nakaoka S, Takeuchi Y, et al. Immune impairment thresholds in HIV infection. Immunology Letters, 2009, 123(2): 149-154 doi: 10.1016/j.imlet.2009.03.007 pmid: 19428563
[19]	Elaiw A M, Raezah A A, Azoz S A. Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Advances in Difference Equations, 2018, Atricle number 414
[20]	Krishnapriya P, Pitchaimani M. Modeling and bifurcation analysis of a viral infection with time delay and immune impairment. Japan Journal of Industrial and Applied Mathematics, 2017, 34(1): 99-139
[21]	Hale J, Lunel S V. An Introduction to Functional Differential Equations. Hoboken: Mathematical Methods in the Applied Sciences, 1993
[22]	Zhao X Q. Basic reproduction ratios for periodic compartmental models with time delay. Journal of Dynamics and Differential Equations, 2017, 29(1): 67-82
[23]	Wang J L, Guo M, Liu X N, et al. Threshold dynamics of HIV-1 virus model with cell-to-cell transmission, cell-mediated immune responses and distributed delay. Applied Mathematics and Computation, 2016, 291: 149-161
[24]	Wang J L, Pang J M, Kuniya T, et al. Global threshold dynamics in a five-dimensional virus model with cell-mediated, humoral immune responses and distributed delays. Applied Mathematics and Computation, 2014, 241: 298-316