含参数 Nabla 积分比和变限含参数 Nabla 积分比的单调性法则及其应用

摘要/Abstract

摘要：

利用时标理论中的 Nabla 积分建立了含参数 Nabla 积分比

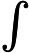
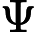
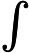
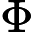
$s\mapsto \frac{\int_\alpha^\beta \Psi(s,v) \nabla v}{\int_\alpha^\beta \Phi(s,v) \nabla v} \quad \text{和} \quad s\mapsto \frac{\int_{v_0}^\infty \Psi(s,v) \nabla v}{\int_{v_0}^\infty \Phi(s,v) \nabla v}$

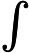
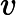
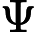
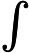
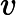
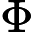
以及变限含参数 Nabla 积分比

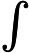
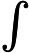
$s\mapsto \frac{\int_{s}^\infty \psi(v) w(s,v) \nabla v }{\int_{s}^\infty \phi(v) w(s,v) \nabla v} \quad \text{和} \quad s\mapsto \frac{\int_{v_0}^{s} \psi(v) w(s,v) \nabla v }{\int_{v_0}^{s} \phi(v) w(s,v) \nabla v}$

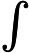
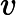
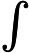
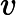
的单调性法则. 在含参数 Nabla 积分比部分中, 还详细研究了一些特殊情形, 包括时标下的多项式之比以及 Nabla 拉普拉斯变换之比. 利用这些单调性法则, 证明了函数 $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{J}_{u_i}(s)}{n \mathcal{J}_{\bar{u}}(s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{J}_{v}(u_is)}{n \mathcal{J}_{v}(\bar{u}s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n K_{u_i}(s)}{n K_{\bar{u}}(s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{Y}_{u_i}(s)}{n \mathcal{Y}_{\bar{u}}(s)}$ 和 $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{Y}_{v}(u_is)}{n \mathcal{Y}_{v}(\bar{u}s)}$ 的单调性, 其中 $\bar{u}=\sum\limits_{i=1}^n u_i/n$ , $I_u(\cdot), K_u(\cdot)$ 分别为第一类和第二类修正的贝塞尔函数, $\mathcal{J}_u(s):= \big( \frac{s}{2} \big)^{-u} I_{u}(s)$ 和 $\mathcal{Y}_u(s):=K_u(s)-K_0(s)$ .

关键词: 单调性法则, 时标, Nabla 积分, 修正贝塞尔函数, 拉普拉斯变换

Abstract:

Using the Nabla integral on time scales, this paper establishes the monotonicity rules for the ratios of parametric Nabla integrals

$s\mapsto \frac{\int_\alpha^\beta \Psi(s,v) \nabla v}{\int_\alpha^\beta \Phi(s,v) \nabla v} \quad \text{and} \quad s\mapsto \frac{\int_{v_0}^\infty \Psi(s,v) \nabla v}{\int_{v_0}^\infty \Phi(s,v) \nabla v}$

and the ratios of the parametric Nabla integrals with variable limits

$s\mapsto \frac{\int_{s}^\infty \psi(v) w(s,v) \nabla v }{\int_{s}^\infty \phi(v) w(s,v) \nabla v} \quad \text{and} \quad s\mapsto \frac{\int_{v_0}^{s} \psi(v) w(s,v) \nabla v }{\int_{v_0}^{s} \phi(v) w(s,v) \nabla v}.$

In the part of monotonicity rules for the ratios of parametric Nabla integrals, some different special cases are considered in detail, including the ratio of two polynomials on time scales and the ratio of two Nabla Laplace transforms. Using these monotonicity rules, the monotonicity of the functions $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{J}{u_i}(s)}{n \mathcal{J}{\bar{u}}(s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{J}{v}(u_is)}{n \mathcal{J}{v}(\bar{u}s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n K_{u_i}(s)}{n K_{\bar{u}}(s)}$ , $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{Y}{u_i}(s)}{n \mathcal{Y}{\bar{u}}(s)}$ and $s\mapsto\frac{\sum\limits_{i=1}^n \mathcal{Y}{v}(u_is)}{n \mathcal{Y}{v}(\bar{u}s)}$ is proved, where $\bar{u}=\sum\limits_{i=1}^n u_i/n$ , $I_u(\cdot), K_u(\cdot)$ are the modified Bessel functions of the first and second kind, respectively, $\mathcal{J}_u(s):= \big( \frac{s}{2} \big)^{-u} I_{u}(s)$ and $\mathcal{Y}_u(s):=K_u(s)-K_0(s)$ .

Key words: Monotonicity rules, Time scales, Nabla integral, Modified Bessel functions, Laplace transforms

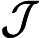
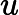
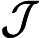
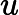
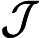
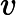
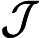
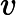
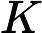
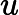
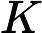
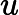
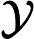
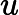
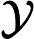
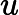
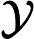
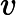
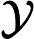
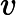
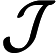
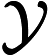
中图分类号:

O171

田景峰, 毛忠旋, 孙龙发. 含参数 Nabla 积分比和变限含参数 Nabla 积分比的单调性法则及其应用[J]. 数学物理学报, 2024, 44(2): 298-312.

Tian Jingfeng, Mao Zhongxuan, Sun Longfa. Monotonicity Rules of the Ratios of Parametric Nabla Integrals and Parametric Nabla Integrals with Variable Limits and Their Applications[J]. Acta mathematica scientia,Series A, 2024, 44(2): 298-312.

参考文献 36

[1]	Biernacki M, Krzyż J. On the monotonicity of certain functionals in the theory of analytic functions. Ann Univ Mariae Curie-Skł lodowska, Sect A, 1955, 9: 135-147
[2]	Cheeger J, Gromov M, Taylor J. Finite propagation speed, kernel estimates for functions of the Laplace operator, and the geometry of complete Riemannian manifolds. J Differ Geom, 1982, 17(1): 15-53
[3]	Yang Z H, Chu Y M, Wang M K. Monotonicity criterion for the quotient of power series with applications. J Math Anal Appl, 2015, 428(1): 587-604 doi: 10.1016/j.jmaa.2015.03.043
[4]	Yang Z H, Tian J F. Monotonicity rules for the ratio of two Laplace transforms with applications. J Math Anal Appl, 2019, 470(2): 821-845 doi: 10.1016/j.jmaa.2018.10.034
[5]	Qi F. Decreasing properties of two ratios defined by three and four polygamma functions. C R Math Acad Sci Paris, 2022, 360: 89-101
[6]	Mao Z X, Tian J F. Monotonicity and complete monotonicity of some functions involving the modified Bessel functions of the second kind. C R Math Acad Sci Paris, 2023, 361: 217-235
[7]	董迎辉, 徐亚娟. 障碍分红策略下的相关双边跳扩散模型. 数学学报, 2014, 57(3): 581-592 doi: 10.12386/A2014sxxb0054
	Dong Y H, Xu Y J, Correlated two-sided jump-diffusion model under the barrier dividend. Acta Math Sin, 2014, 57(3): 581-592 doi: 10.12386/A2014sxxb0054
[8]	邓继勤, 邓子明. 分数阶微分方程非局部柯西问题解的存在和唯一性. 数学物理学报, 2016, 36A(6): 1157-1164
	Deng J Q, Deng Z M. Existence and uniquencess of solutions for nonlocal cauchy problem for fractional evolution equations. Acta Math Sci, 2016, 36A(6): 1157-1164
[9]	郭庭光, 徐志庭. 带有扩散项和接种的传染病模型的行波解. 数学物理学报, 2017, 37A(6): 1129-1147
	Guo T G, Xu Z T. Existence of traveling waves in a spatial infectious disease model with vaccination. Acta Math Sci, 2017, 37A(6): 1129-1147
[10]	孙海江, 王延杰, 刘伟宁. 基于自适应平台阈值和拉普拉斯变换的红外图像增强. 中国光学, 2011, 4(5): 474-479
	Sun H J, Wang Y J, Liu W N. Enhancement of infrared images based on adaptive platform threshold and Laplace transformation. Chin Optics, 2011, 4(5): 474-479
[11]	苗启广, 王宝树. 基于改进的拉普拉斯金字塔变换的图像融合方法. 光学学报, 2007, 27(9): 1605-1610
	Miao Q G, Wang B S. Multi-Sensor image fusion based on improved Laplacian pyramid transform. Acta Optical Sin, 2007, 27: 1605-1610
[12]	Sahbani J. Quantitative uncertainty principles for the canonical Fourier-Bessel transform. Acta Math Sin (Engl Ser), 2022, 38(2): 331-346 doi: 10.1007/s10114-022-1008-7
[13]	Jain P, Basu C, Panwar V. On the ( $p, q$ )-Mellin transform and its applications. Acta Math Sci, 2021, 41B: 1719-1732
[14]	Weiss L, McDonough R N. Prony's method, $Z$ -transforms and Padé approximation. SIAM Rev, 1963, 5(2): 145-149 doi: 10.1137/1005035
[15]	Hilger S. Ein Maßkettenkalkül mit anwendung auf zentrumsmannigfaltigkeiten[D]. Würzburg: Universität Würzburg, 1988
[16]	Bohner M, Peterson A. Dynamic Equations on Time Scales. Boston: Springer, 2001
[17]	Bohner M, Peterson A. Advances in Dynamic Equations on Time Scales. Boston: Springer, 2003
[18]	Bohner M, Georgiev S G. Multivariable Dynamic Calculus on Time Scales. Cham: Springer, 2016
[19]	欧柳曼, 朱思铭. 时标动力方程的稳定性分析. 数学物理学报, 2008, 28A(2): 308-319
	Ou L M, Zhu S M, Stable analysis for dynamic equations on time scales. Acta Math Sci, 2008, 28A(2): 308-319
[20]	罗华. 时标线性加权 Sturm-Liouville 特征值问题的谱理论分析. 数学物理学报, 2017, 37A(3): 427-449
	Luo H. Spectral theory of linear weighted Sturm-Liouville eigenvalue problems. Acta Math Sci, 2017, 37A(3): 427-449
[21]	李继猛, 杨甲山. 时标上二阶拟线性延迟阻尼动态系统的动力学行为分析. 应用数学学报, 2020, 43(5): 853-864 doi: 10.12387/C2020062
	Li J M, Yang J S. Dynamical behavior of second-order quasilinear delay damped dynamic equations on time scales. Acta Math Appl Sin, 2020, 43(5): 853-864 doi: 10.12387/C2020062
[22]	张萍, 杨甲山. 时标上具正负系数的三阶阻尼动力方程的振动性. 应用数学学报, 2021, 44(5): 632-645 doi: 10.12387/C2021045
	Zhang P, Yang J S. Oscillation of third-order damped dynamic equations with positive and negative coefficients on time scales. Acta Math Appl Sin, 2021, 44(5): 632-645 doi: 10.12387/C2021045
[23]	Matthews T. Probability theory on time scales and applications to finance and inequalities[D]. Rolla: Missouri University of Science and Technology, 2011
[24]	Georgiev S G, Erhan İ M. The Taylor series method and trapezoidal rule on time scales. Appl Math Comput, 2020, 378: 125200
[25]	Georgiev S G, Erhan İ M. Lagrange interpolation on time scales. J Appl Anal Comput, 2022, 12(4): 1294- 1307
[26]	Bartosiewicz Z, Pawluszewicz E. Realizations of nonlinear control systems on time scales. IEEE T Automat Contr, 2008, 53(2): 571-575 doi: 10.1109/TAC.9
[27]	詹再东. 时标型动态微分系统的最优控制问题及其应用[D]. 杭州: 浙江大学, 2012
	Zhan Z D. Optimal control problem governed by dynamic differential systems on arbitary time scales and applications[D]. Hangzhou: Zhejiang University, 2012
[28]	Xiao Q, Zeng Z. Scale-limited lagrange stability and finite-time synchronization for memristive recurrent neural networks on time scales. IEEE T Cybernetics, 2017, 47(10): 2984-2994 doi: 10.1109/TCYB.2017.2676978 pmid: 28362603
[29]	肖强. 时标型网络系统的动力学分析与控制[D]. 武汉: 华中科技大学, 2019
	Xiao Q. Dynamic analysis and control of timescale-type networked system[D]. Wuhan: Huazhong University of Science and Technology, 2019
[30]	Davis J M, Gravagne I A, Marks R J. Convergence of unilateral Laplace transforms on time scales. Circ Syst Signal Pr, 2010, 29(5): 971-997 doi: 10.1007/s00034-010-9182-8
[31]	Benkhettou N, Brito da Cruz A, Torres D. A fractional calculus on arbitrary time scales: Fractional differentiation and fractional integration. Signal Process, 2015, 107: 230-237
[32]	王竹溪, 郭敦仁. 特殊函数概论. 北京: 北京大学出版社, 2000
	Wang Z X, Guo D R. Introduction to Special Functions. Beijing: Peking University Press, 2000
[33]	Nikiforov A F, Uvarov V B. Special Functions of Mathematical Physics. Basel: Birkhäuser Verlag, 1988
[34]	Rahmat M R S. Integral transform methods for solving fractional dynamic equations on time scales. Abstr Appl Anal, Hindawi, 2014, 2014: 261348
[35]	Anderson D R. Taylor polynomials for nabla dynamic equations on time scales. Panamer Math J, 2002, 12(4): 17-28
[36]	Yang Z H, Qian W M, Chu Y M, et al. Monotonicity rule for the quotient of two functions and its application. J Inequal Appl, 2017, 2017: 1-13 doi: 10.1186/s13660-017-1388-x