数学物理学报 ›› 2023, Vol. 43 ›› Issue (6): 1774-1788.
一类具有时滞的 Gierer-Meinhardt 活化抑制模型的分支分析
- 1陕西科技大学数学与数据科学学院 西安 710021
2西安交通大学数学与统计学院 西安 710049
-
收稿日期:2022-08-08修回日期:2023-07-07出版日期:2023-12-26发布日期:2023-11-16 -
通讯作者:*袁海龙,E-mail:yuanhailong@sust.edu.cn -
基金资助:国家自然科学基金(11901370);陕西省自然科学基础研究计划项目基金(2019JQ-516);陕西省教育厅专项科研计划项目(19JK0142);国家博士后基金(2019M653578);陕西省科协人才托举项目(20200508)
Bifurcation Analysis of a Class of Gierer-Meinhardt Activation Inhibition Model with Time Delay
- 1School of Mathematics and Data Science, Shanxi University of Science and Technology, Xi'an 710021
2School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an 710049
-
Received:2022-08-08Revised:2023-07-07Online:2023-12-26Published:2023-11-16 -
Supported by:NSFC(11901370);Natural Science Basic Research Plan in Shannxi Province(2019JQ-516);Natural Science Foundation of Shanxi Provincial Department of Education grant(19JK0142);Natural Science Foundation of China(2019M653578);Shanxi Provincial Association for Science and Technology(20200508)
摘要:
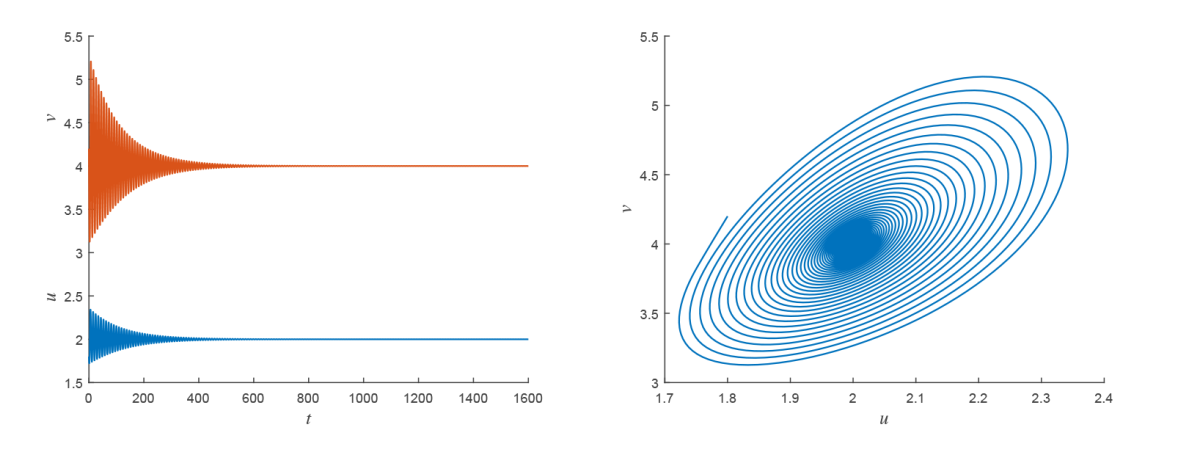
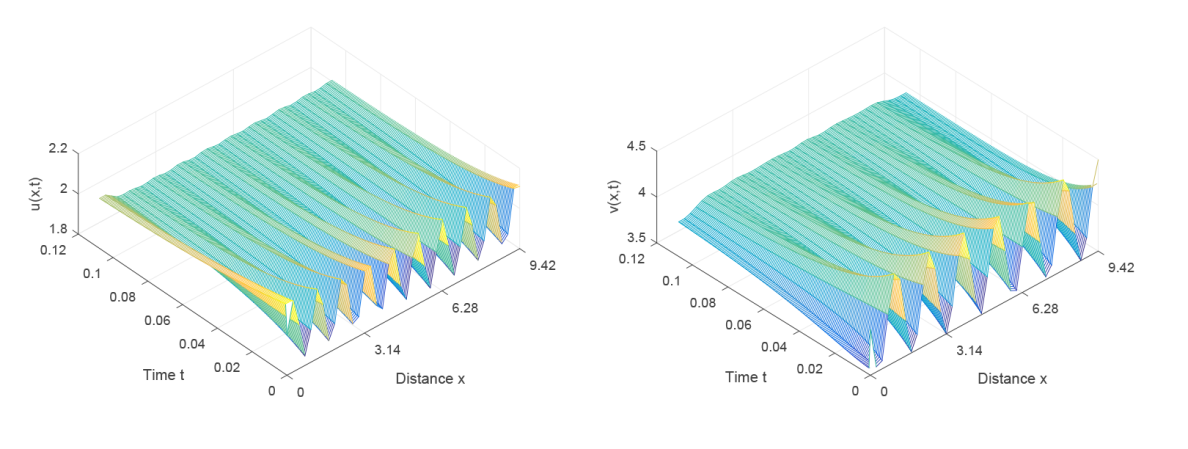
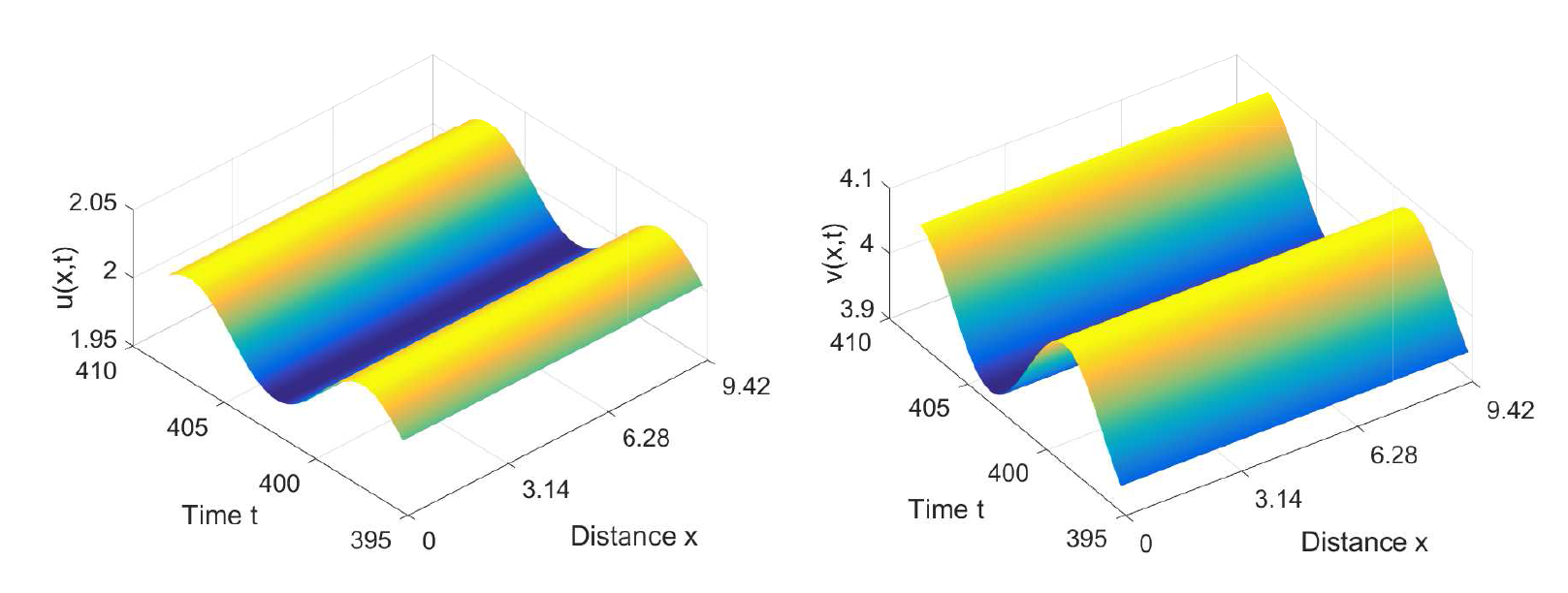
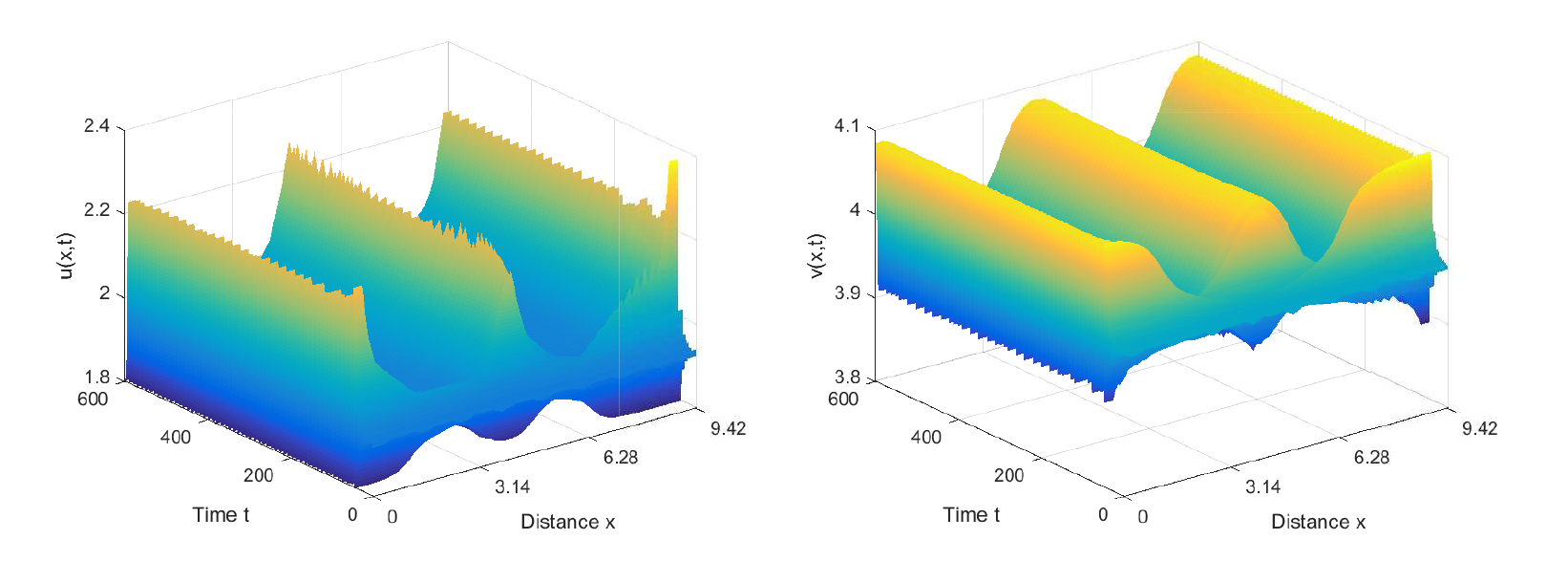
该文研究了一类在齐次 Neumann 边界条件下具有时滞扩散的 Gierer-Meinhardt 活化抑制模型. 首先, 利用谱理论得到了该模型正平衡点的局部渐近稳定性; 其次, 以时滞为分支参数, 研究了该模型 Hopf 分支的存在性; 接着, 根据偏泛函微分方程的中心流形定理和正规型理论, 得到了该 Hopf 分支方向和分支周期解的稳定性; 最后, 利用 Matlab 软件, 模拟了该系统在临界点附近经历的 Hopf 分支.
中图分类号:
- O175.12
引用本文
马亚妮, 袁海龙. 一类具有时滞的 Gierer-Meinhardt 活化抑制模型的分支分析[J]. 数学物理学报, 2023, 43(6): 1774-1788.
Ma Yani, Yuan Hailong. Bifurcation Analysis of a Class of Gierer-Meinhardt Activation Inhibition Model with Time Delay[J]. Acta mathematica scientia,Series A, 2023, 43(6): 1774-1788.
使用本文
| [1] | 欧阳颀. 反应扩散系统中的斑图动力学. 上海: 上海科技教育出版社, 2000 |
| Ou Y X. Turing Dynamics in Reaction Diffusion Systems. Shanghai: Shanghai Science and Technology Education Press, 2000 | |
| [2] |
Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik, 1972, 12: 30-39
pmid: 4663624 |
| [3] |
Gierer A, Meinhardt H. Application of a theory of biological pattern formation based on lateral inhibition. J Cell Sci, 1974, 15(2): 321-346
doi: 10.1242/jcs.15.2.321 pmid: 4859215 |
| [4] | Gierer A, Meinhardt H. Generation and regeneration of sequence of structures during morphogenesis. J Theor Biol, 1980, 3: 429-450 |
| [5] |
Wei J C, Winter M. Spikes for the Gierer-Meinhardt system in two dimensions: The strong coupling case. J Differ Equ, 2002, 178(2): 478-518
doi: 10.1006/jdeq.2001.4019 |
| [6] |
Ni W M, Suzuki K, Takagi I. The dynamics of a kinetic activator-inhibitor system. J Differ Equ, 2006, 229(2): 426-465
doi: 10.1016/j.jde.2006.03.011 |
| [7] |
Takashi M, Maini P K. Speed of pattern appearance in reaction-diffusion models: Implications in the pattern formation of limb bud mesenchyme cells. Bull Math Biol, 2004, 66(4): 627-649
doi: 10.1016/j.bulm.2003.09.009 |
| [8] |
Gonpot P, Collet J S A J, Sookia N U H. Gierer-Meinhardt model: Bifurcation analysis and pattern formation. Trends Appl Sci Res, 2008, 3: 115-128
doi: 10.3923/tasr.2008.115.128 |
| [9] |
Yang R, Song Y L. Spatial resonance and Turing-Hopf bifurcations in the Gierer-Meinhardt model. Nonlinear Anal: Real World Appl, 2016, 31: 356-387
doi: 10.1016/j.nonrwa.2016.02.006 |
| [10] | 杨文彬, 吴建华. 空间齐次和非齐次下活化-抑制模型动力学分析. 数学物理学报, 2017, 37A(22): 390-400 |
| Yang W B, Wu J H. Dynamics analysis of activation-inhibition models under spatial homogeneous and heterogeneou. Acta Math Sci, 2017, 37A(22): 390-400 | |
| [11] |
Liu J X, Yi F Q, Wei J J. Multiple bifurcation analysis and spatiotemporal patterns in a  doi: 10.1142/S0218127410026289 |
| [12] | Wang J L, Hou X J, Jing Z J. Stripe and spot patterns in a Gierer Meinhardt activator-inhibitor model with different sources. Int J Bifurcat Chaos, 2015, 25(8): 108-155 |
| [13] |
Wang J F, Wei J J, Shi J P. Global bifurcation analysis and pattern formation in homogeneous diffusive predator-prey systems. J Diff Equ, 2016, 260(4): 3495-3523
doi: 10.1016/j.jde.2015.10.036 |
| [14] | 叶其孝, 李正元, 王明新, 吴雅萍. 反应扩散方程引论. 北京: 科学出版社, 2011 |
| Ye Q X, Li Z Y, Wang M X, Wu Y P. Introduction to Reaction-Diffusion Equations. Beijing: Science Press, 2011 | |
| [15] |
Yi F Q, Wei J J, Shi J P. Diffusion-Driven instability and bifurcation in the Lengyel-Epstein system. Nonlinear Anal: Real World Appl, 2008, 9(3): 1038-1051
doi: 10.1016/j.nonrwa.2007.02.005 |
| [16] |
Galkhar S, Negi K, Sahani S K. Effects of seasonal growth on ratio dependent delayed prey predator system. Commun Nonlinear Sci Numer Simul, 2009, 14(3): 850-862
doi: 10.1016/j.cnsns.2007.10.013 |
| [17] |
Guan X N, Wang W M, Cai Y L. Spatiotemporal dynamics of a leslie-gower predator-prey model incorporating a prey refuge. Nonlinear Anal: Real World Appl, 2011, 12(4): 2385-2395
doi: 10.1016/j.nonrwa.2011.02.011 |
| [18] |
Lee S S, Gaffney E A, Monk N A M. The influence of gene expression time delays on Gierer-Meinhardt pattern formation systems. Bull Math Biol, 2010, 72(8): 2139-2160
doi: 10.1007/s11538-010-9532-5 |
| [19] |
Dutta S, Ray D S. Effects of delay in a reaction-diffusion system under the influence of an electric field. Phys Rev E, 2008, 77(3): 036202
doi: 10.1103/PhysRevE.77.036202 |
| [20] |
Ghosh P. Control of the Hopf-turing transition by time-delayed global feedback in a reaction-diffusion System. Phys Rev E, 2011, 84: 016222
doi: 10.1103/PhysRevE.84.016222 |
| [21] |
Ghosh P, Sen S, Ray D S. Reaction-Cattaneo systems with fluctuating relaxation time. Phys Rev E, 2010, 81(2): 026205
doi: 10.1103/PhysRevE.81.026205 |
| [22] |
Kyrychko Y, Blyuss K B, Hogan S J, et al. Control of spatiotemporal patterns in the Gray-Scott model. Chaos, 2009, 19(4): 043126
doi: 10.1063/1.3270048 |
| [23] |
Sen S, Ghosh P, Syed S, et al. Time-Delay-Induced instabilities in reaction diffusion systems. Phys Rev E, 2008, 80(4): 046212
doi: 10.1103/PhysRevE.80.046212 |
| [24] | Suleiman A L. Stability analysis of the Gierer-Meinhardt system with activator degradation. Dutse J Pure Appl Sci, 2016, 2(1): 48-54 |
| [25] |
Li C C, Guo S J. Stability and bifurcation of a delayed reaction-diffusion model with robin boundary condition in heterogeneous environment. Int J Bifurcat Chaos, 2023, 33(2): 2350018
doi: 10.1142/S0218127423500189 |
| [26] | Wen T T, Wang X L, Zhang G H. Hopf bifurcation in a two-species reaction-diffusion-advection competitive model with nonlocal delay. Commun Pur Appl Anal, 2023, 22(5): 1517-1544 |
| [27] | Ma L, Wei D. Hopf bifurcation of a delayed reaction-diffusion model with advection term. Nonlinear Anal: An Inter Mult J, 2021, 212(2): 112455 |
| [28] | 王雅迪, 袁海龙. 一类具有时滞的营养-微生物扩散模型的 Hopf 分支研究. 西南师范大学学报(自然科学版), 2023, 48(5): 1-13 |
| Wang Y D, Yuan H L. Hopf bifurcation of a nutritional microbial diffusion model with time delay. Journal of Southwest Normal University (Natural Science Edition), 2023, 48(5): 1-13 | |
| [29] |
Dong Y Y, Li S B, Zhang S L. Hopf bifurcation in a reaction-diffusion model with Degn-Harrison reaction scheme. Nonlinear Anal: Real World Appl, 2017, 33: 284-297
doi: 10.1016/j.nonrwa.2016.07.002 |
| [30] | Lin X D, So J W H, Wu J H. Center manifolds for partial differential equations with delay. P Roy Soc Edinb A: Math, 1992, 122(3/4): 237-254 |
| [31] | Wu J H. Theory and Applications of Partial Functional Differential Equations. New York: Springer-Verlag, 1996 |
| [32] | 万阿英, 衣风岐, 郑立飞. 一类扩散的 Gierer-Meinhardt 的模型的振动模式和 Hopf 分支分析. 数学物理学报, 2015, 35A(2): 381-394 |
| Wan A Y, Yi F Q, Zeng L F. Oscillating patterns and Hopf bifurcation analysis of a class of diffusion Gierer-Meinhardt models. Acta Math Sci, 2015, 35A(2): 381-394 |
| [1] | 徐斐, 张勇. 分数阶 Burgers 方程时间周期弱解的唯一性与渐近稳定性[J]. 数学物理学报, 2023, 43(6): 1710-1722. |
| [2] | 刘国威, 王启玲. 一类时滞非牛顿流体在二维无界域上的适定性[J]. 数学物理学报, 2023, 43(6): 1789-1802. |
| [3] | 庞玉婷, 赵东霞. 星形明渠网络系统的 PDP 反馈控制和指数镇定[J]. 数学物理学报, 2023, 43(6): 1803-1813. |
| [4] | 范示示, 李海侠, 路银豆. 具有捕获项的 Beddington-DeAnglis 型捕食-食饵扩散模型的动力学分析[J]. 数学物理学报, 2023, 43(6): 1929-1942. |
| [5] | 庞玉婷,赵东霞,赵鑫,高彩霞. 一类 2 |
| [6] | 廖远康. 粘性依赖于密度的一维等熵可压缩 Navier-Stokes 方程组粘性激波的非线性稳定性[J]. 数学物理学报, 2023, 43(4): 1149-1169. |
| [7] | 何旭阳,毛明志,张腾飞. 一类具有泊松跳的脉冲中立型随机泛函微分方程的存在性及稳定性研究[J]. 数学物理学报, 2023, 43(4): 1221-1243. |
| [8] | 李继泽,邱吉秀,周永辉. 受观察噪声影响的不可料非线性滤波方程及线性滤波稳定性[J]. 数学物理学报, 2023, 43(4): 1244-1254. |
| [9] | 张海群. 有限理性与一类群体博弈弱有效Nash均衡的稳定性[J]. 数学物理学报, 2023, 43(4): 1311-1320. |
| [10] | 黎小丽,陈晓莉. 部分耗散的三维Boussinesq方程在静力平衡附近的稳定性和指数衰减[J]. 数学物理学报, 2023, 43(3): 754-770. |
| [11] | 武文俊,杨光惠,房才雅,杨辉. 主从群体博弈合作均衡的通有稳定性[J]. 数学物理学报, 2023, 43(3): 921-929. |
| [12] | 康笑东, 范虹霞. 一类具有瞬时脉冲的二阶发展方程的近似可控性[J]. 数学物理学报, 2023, 43(2): 421-432. |
| [13] | 付亲宏, 熊良林, 张海洋, 秦娅, 权沈爱. 具有半马尔可夫跳跃的时变时滞系统的滑模控制研究[J]. 数学物理学报, 2023, 43(2): 549-562. |
| [14] | 刘利利, 王洪刚, 李雅芝. 考虑病毒DNA核衣壳和细胞间传播的一般HBV扩散模型[J]. 数学物理学报, 2023, 43(2): 604-624. |
| [15] | 宋慧娟, 黄倩, 王泽佳. 具周期营养供给的血管化肿瘤生长模型的渐近分析[J]. 数学物理学报, 2023, 43(1): 261-273. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 206
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 77
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|