具有不同类型阻尼弱耦合板方程的间接镇定和最优衰减率

摘要/Abstract

摘要：

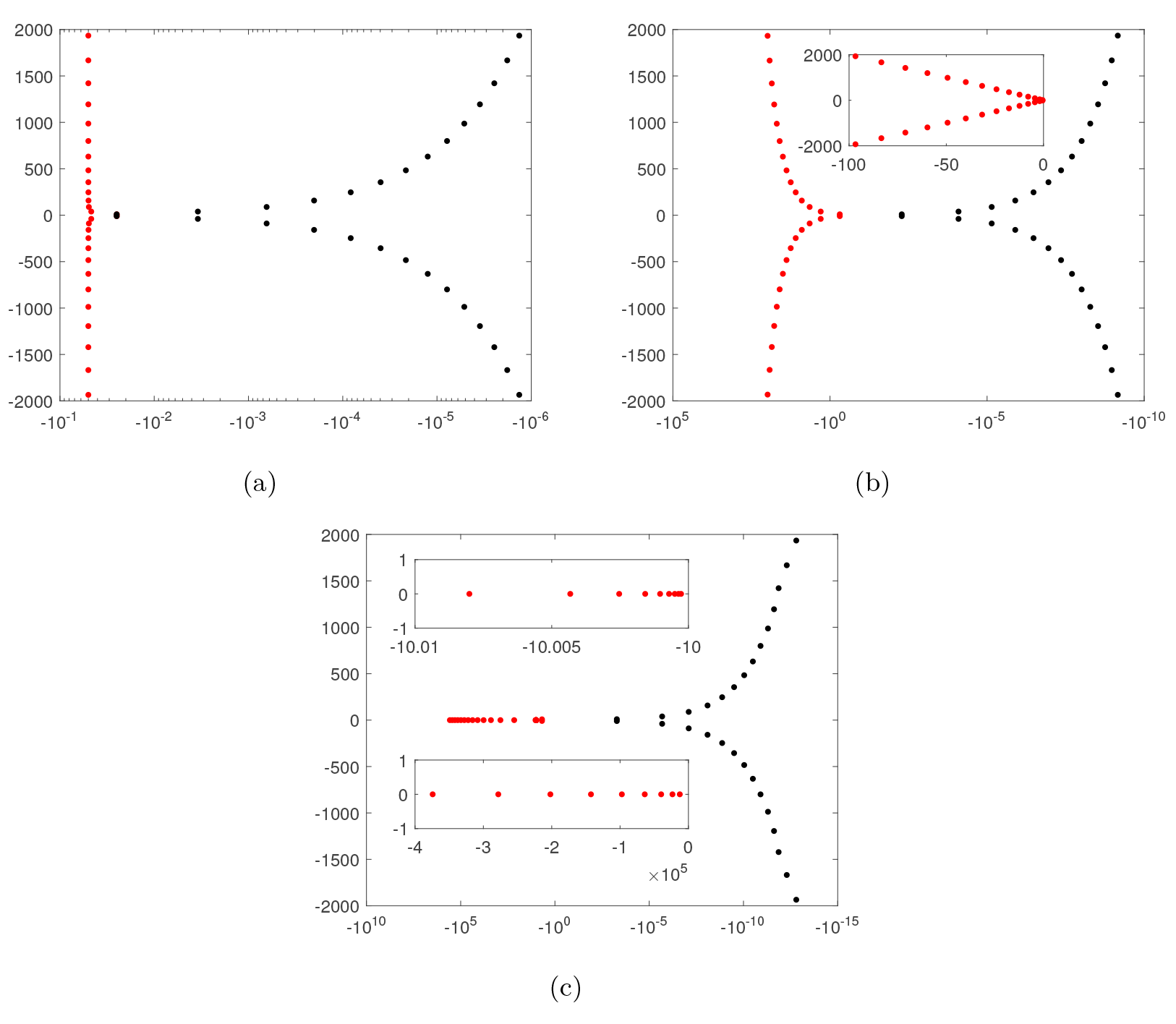
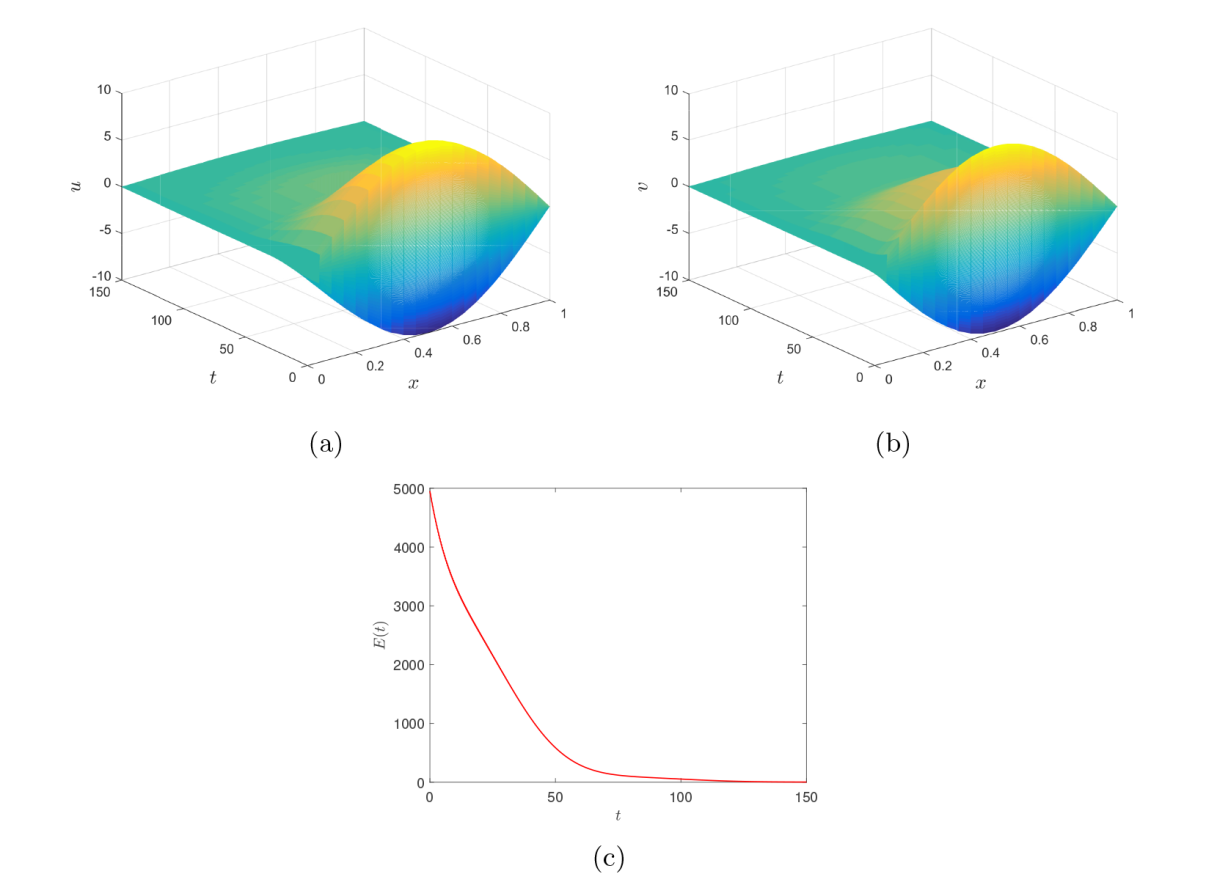
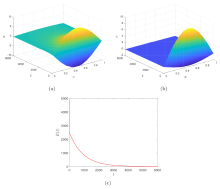
该文主要研究弱耦合弹性板系统的稳定性和最优衰减率, 其中系统中仅有一块板带有阻尼 (粘性阻尼、结构阻尼或 Kelvin-Voigt 阻尼). 基于频域方法和对系统算子细致的谱分析, 导出了系统的最优多项式衰减率. 此外, 还确定了系统的最优衰减率与阻尼阶数之间的关系, 并且发现了一个有趣的现象, 即间接阻尼的阶数越高, 弱耦合板系统衰减越慢. 最后, 通过数值模拟对理论结果进行了验证.

关键词: 耦合弹性板, 间接镇定, 最优多项式衰减, 谱分析, 频域方法

Abstract:

This work is concerned with the stabilization and optimal decay rates of a weakly coupled (coupling through displacements) elastic plate system, where the damping (viscous damping, structural damping or Kelvin-Voigt damping) is actuated at only one of the two plates. The optimal polynomial decay rate is derived based on the frequency domain approach and detailed spectral analysis of the system operator. Moreover, the relationship between the optimal decay rates of the system and the order of damping is identified. Besides, an interesting phenomenon is found that the higher the order of indirect damping is actuated, the slower polynomial decay rate of the weakly coupled plate system achieves. Finally, some numerical simulations are presented to verify the theoretical results.

Key words: Coupled elastic plate, Indirect stabilization, Optimal polynomial decay, Spectral analysis, Frequency domain analysis

中图分类号:

O231.4

韩忠杰, 贺以恒, 赵志学. 具有不同类型阻尼弱耦合板方程的间接镇定和最优衰减率[J]. 数学物理学报, 2023, 43(6): 1681-1698.

Han Zhongjie, He Yiheng, Zhao Zhixue. Indirect Stabilization and Optimal Decay Rates of Weakly Coupled Plates with Various Types of Damping[J]. Acta mathematica scientia,Series A, 2023, 43(6): 1681-1698.

图/表 4

参考文献 38

[1]	Akil M, Badawi H, Nicaise S. Stability results of locally coupled wave equations with local Kelvin-Voigt damping: Cases when the supports of damping and coupling coefficients are disjoint. Computational and Applied Mathematics, 2022, 41: Article number 240
[2]	Akil M, Issa I, Wehbe A. Energy decay of some boundary coupled systems involving wave Euler-Bernoulli beam with one locally singular fractional Kelvin-Voigt damping. Math Control Relat Fields, 2023, 13(1): 330-381 doi: 10.3934/mcrf.2021059
[3]	Alabau-Boussouira F. Indirect boundary stabilization of weakly coupled hyperbolic systems. SIAM J Control Optim, 2002, 41(2): 511-541 doi: 10.1137/S0363012901385368
[4]	Alabau-Boussouira F, Cannarsa P, Guglielmi R. Indirect stabilization of weakly coupled systems with hybrid boundary conditions. Math Control Relat Fields, 2011, 1(4): 413-436 doi: 10.3934/mcrf.2011.1.413
[5]	Alabau F, Cannarsa P, Komornik V. Indirect internal stabilization of weakly coupled evolution equations. J Evol Equ, 2002, 2: 127-150 doi: 10.1007/s00028-002-8083-0
[6]	Alabau-Boussouira F, Léautaud M. Indirect stabilization of locally coupled wave-type systems. ESAIM Control Optim Calc Var, 2012, 18(2): 548-582 doi: 10.1051/cocv/2011106
[7]	Alabau-Boussouira F, Wang Z, Yu L. A one-step optimal energy decay formula for indirectly nonlinearly damped hyperbolic systems coupled by velocities. ESAIM Control Optim Calc Var, 2017, 23: 721-749 doi: 10.1051/cocv/2016011
[8]	Ammari K, Fathi H, Robbiano L. Fractional-Feedback stabilization for a class of evolution systems. J Differential Equations, 2020, 268: 5751-5791 doi: 10.1016/j.jde.2019.11.022
[9]	Ammari K, Shel F, Tebou L. Regularity and stability of the semigroup associated with some interacting elastic systems I: A degenerate damping case. J Evol Equ, 2021, 21: 4973-5002 doi: 10.1007/s00028-021-00738-7
[10]	Borichev A, Tomilov Y. Optimal polynomial decay of functions and operator semigroups. Math Ann, 2010, 347: 455-478 doi: 10.1007/s00208-009-0439-0
[11]	Chen G, Russell D L. A mathematical model for linear elastic systems with structural damping. Quart Appl Math, 1982, 39(4): 433-454 doi: 10.1090/qam/1982-39-04
[12]	Cui Y, Wang Z. Asymptotic stability of wave equations coupled by velocities. Math Control Relat Fields, 2016, 6(3): 429-446 doi: 10.3934/mcrf
[13]	Fernández Sare H D, Liu Z, Racke R. Stability of abstract thermoelastic systems with inertial terms. J Differential Equations, 2019, 267(12): 7085-7134 doi: 10.1016/j.jde.2019.07.015
[14]	Fu X. Sharp decay rates for the weakly coupled hyperbolic system with one internal damping. SIAM J Control Optim, 2012, 50(3): 1643-1660 doi: 10.1137/110833051
[15]	Fu X LüQ. Stabilization of the weakly coupled wave-plate system with one internal damping. Vietnam J Math, 2021, 49: 767-786 doi: 10.1007/s10013-021-00493-9
[16]	Guglielmi R. Indirect stabilization of hyperbolic systems through resolvent estimates. Evol Equ Control Theory, 2017, 6(1): 59-75
[17]	Hajej A, Hajjej Z, Tebou L. Indirect stabilization of weakly coupled Kirchhoff plate and wave equations with frictional damping. J Math Anal Appl, 2019, 474(1): 290-308 doi: 10.1016/j.jmaa.2019.01.046
[18]	Han Z J, Liu Z. Regularity and stability of coupled plate equations with indirect structural or Kelvin-Voigt damping. ESAIM Control Optim Calc Var, 2019, 25: Article number 51
[19]	Hao J, Liu Z. Stability of an abstract system of coupled hyperbolic and parabolic equations. Z Angew Math Phys, 2013, 64: 1145-1159 doi: 10.1007/s00033-012-0274-0
[20]	Hao J, Liu Z, Yong J. Regularity analysis for an abstract system of coupled hyperbolic and parabolic equations. J Differential Equations, 2015, 259(9): 4763-4798 doi: 10.1016/j.jde.2015.06.010
[21]	Huang F. On the mathematical model for linear elastic systems with analytic damping. SIAM J Control Optim, 1988, 26(3): 714-724 doi: 10.1137/0326041
[22]	Huang F, Liu K. Holomorphic property and exponential stability of the semigroup associated with linear elastic systems with damping. Ann Differ Equ, 1988, 4: 411-424
[23]	Liu Z, Rao B. Frequency domain approach for the polynomial stability of a system of partially damped wave equations. J Math Anal Appl, 2007, 335(2): 860-881 doi: 10.1016/j.jmaa.2007.02.021
[24]	Liu Z, Rao B. Characterization of polynomial decay rate for the solution of linear evolution equation. Z Angew Math Phys, 2005, 56: 630-644 doi: 10.1007/s00033-004-3073-4
[25]	Liu Z, Rao B, Zhang Q. Polynomial stability of the Rao-Nakra beam with a single internal viscous damping. J Differential Equations, 2020, 269(7): 6125-6162 doi: 10.1016/j.jde.2020.04.030
[26]	Liu Z, Zhang Q. Stability and regularity of solution to the Timoshenko beam equation with local Kelvin-Voigt damping. SIAM J Control and Optim, 2018, 56(6): 3919-3947 doi: 10.1137/17M1146506
[27]	Liu Z, Zheng S. Semigroups Associated with Dissipative Systems. Boca Raton: Chapman & Hall/CRC, 1999
[28]	Loreti P, Rao B. Optimal energy decay rate for partially damped systems by spectral compensation. SIAM J Control Optim, 2006, 45(5): 1612-1632 doi: 10.1137/S0363012903437319
[29]	Mansouri S. Boundary stabilization of coupled plate equations. Palest J Math, 2013, 2: 233-242
[30]	Oquendo H P, Suárez F M S. Exact decay rates for coupled plates with partial fractional damping. Z Angew Math Phys, 2019, 70: Article number 88
[31]	Pazy A. Semigroups of Linear Operators and Applications to Partial Differential Equations. New York: Springer-Verlag, 1983
[32]	Rao B. On the sensitivity of the transmission of boundary dissipation for strongly coupled and indirectly damped systems of wave equations. Z Angew Math Phys, 2019, 70: Article number 75
[33]	Russell D L. A general framework for the study of indirect damping mechanisms in elastic systems. J Math Anal Appl, 1993, 173(2): 339-358 doi: 10.1006/jmaa.1993.1071
[34]	Tebou L. Energy decay estimates for some weakly coupled Euler-Bernoulli and wave equations with indirect damping mechanisms. Math Control Relat Fields, 2012, 2(1): 45-60 doi: 10.3934/mcrf.2012.2.45
[35]	Yim J H, Jang B Z. An analytical method for prediction of the damping in symmetric balanced laminated composites. Polymer Composites, 1999, 20: 192-199 doi: 10.1002/pc.v20:2
[36]	Zhang X, Zuazua E. Decay of solutions of the system of thermoelasticity of type III. Commun Contemp Math, 2003, 5: 25-83 doi: 10.1142/S0219199703000896
[37]	Zhang X, Zuazua E. Long-Time behavior of a coupled heat-wave system arising in fluid-structure interaction. Arch Rational Mech Anal, 2007, 184: 49-120 doi: 10.1007/s00205-006-0020-x
[38]	Zhu X. Stabilization of the weakly coupled plate equations with a locally distributed damping. Advances in Difference Equations, 2020, 2020: Article number 230