数学物理学报 ›› 2023, Vol. 43 ›› Issue (5): 1595-1606.
具有媒体报道的 SVIR 传染病模型的生存性分析
- 1福州大学数学与统计学院 福州 350116
2福州大学运筹学与控制论福建省高校重点实验室 福州 350116
3思克莱德大学数学与统计系 格拉斯哥 G1 1XH
-
收稿日期:2022-04-22修回日期:2022-10-31出版日期:2023-10-26发布日期:2023-08-09 -
通讯作者:魏凤英 E-mail:weifengying@fzu.edu.cn -
基金资助:国家自然科学基金-国际(地区)合作与交流项目(61911530398);福建省科技厅项目(2021L3018);福建省自然科学基金(2021J01621);英国皇家学会(WM160014);英国皇家学会(英国皇家学会沃尔夫森研究优异奖);英国皇家学会和牛顿基金(NA160317);英国皇家学会和牛顿基金(皇家学会-牛顿高级奖学金);工程和物理科学研究委员会(EP/K503174/1)
Survival Analysis of an SVIR Epidemic Model with Media Coverage
Li Dan1,Wei Fengying2,*( ),Mao Xuerong3
),Mao Xuerong3
- 1School of Mathematics and Statistics, Fuzhou University, Fuzhou 350116
2Key Laboratory of Operations Research and Control of Universities in Fujian, Fuzhou University, Fuzhou 350116
3Department of Mathematics and Statistics, University of Strathclyde, Glasgow G1 1XH, UK
-
Received:2022-04-22Revised:2022-10-31Online:2023-10-26Published:2023-08-09 -
Contact:Fengying Wei E-mail:weifengying@fzu.edu.cn -
Supported by:National Natural Science Foundation of China(61911530398);Special Projects of the Central Government Guiding Local Science, Technology Development(2021L3018);Natural Science Foundation of Fujian Province of China(2021J01621);Royal Society, UK(WM160014);Royal Society, UK (Royal Society Wolfson Research Merit Award);Royal Society and the Newton Fund, UK(NA160317);Royal Society and the Newton Fund, UK (Royal Society-Newton Advanced Fellowship);EPSRC, the Engineering and Physical Sciences Research Council(EP/K503174/1)
摘要:
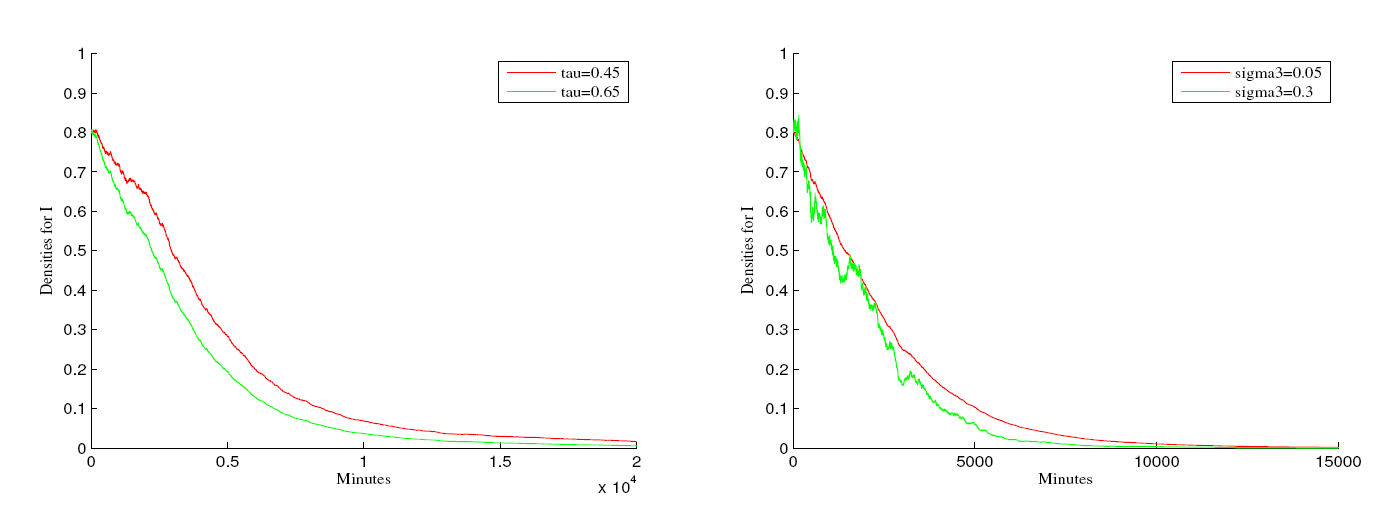
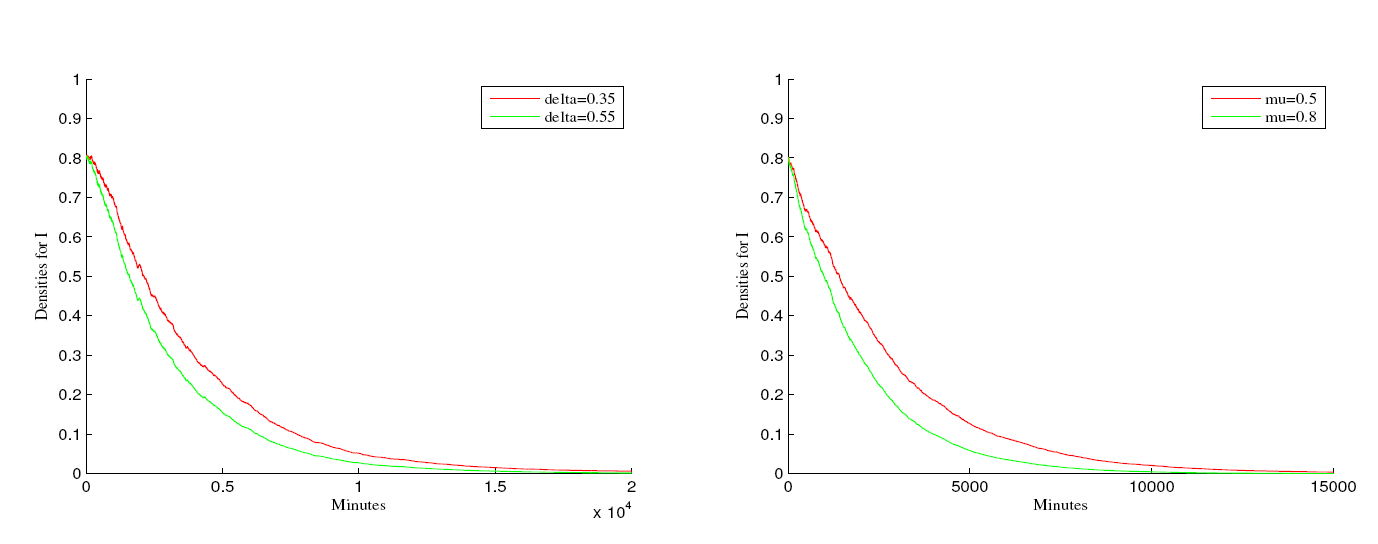
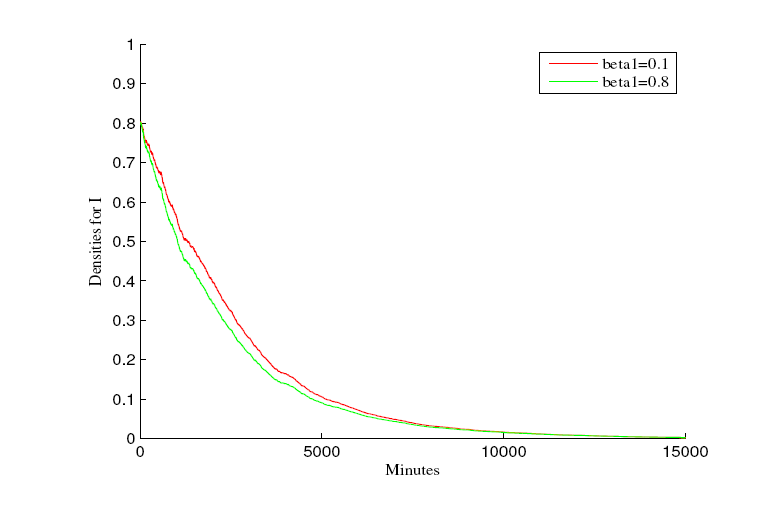
该文研究了具有Logistic增长和媒体报道的饱和发生率的随机SVIR模型. 为了研究模型的动力学性质, 首先证明了随机模型全局正解的存在唯一性, 其次通过构造合适的李雅普诺夫函数, 探究疾病持久和灭绝的充分性条件. 研究表明: 当Rs0>1时, 疾病长时间持续存在. 当Re0<1时, 疾病在流行一段时间后灭绝. 最后, 通过数值模拟验证了以上结论.
中图分类号:
- O175.13
引用本文
李丹,魏凤英,毛学荣. 具有媒体报道的 SVIR 传染病模型的生存性分析[J]. 数学物理学报, 2023, 43(5): 1595-1606.
Li Dan,Wei Fengying,Mao Xuerong. Survival Analysis of an SVIR Epidemic Model with Media Coverage[J]. Acta mathematica scientia,Series A, 2023, 43(5): 1595-1606.
使用本文
| [1] |
Adimy M, Chekroun A, Kuniya T. Traveling waves of a differential-difference diffusive Kermack-McKendrick epidemic model with age-structured protection phase. J Math Anal Appl, 2022, 505(1): 125464
doi: 10.1016/j.jmaa.2021.125464 |
| [2] |
Cao Z W, Feng W, Wen X D. Dynamical behavior of a stochastic SEI epidemic model with saturation incidence and logistic growth. Physica A, 2019, 523: 894-907
doi: 10.1016/j.physa.2019.04.228 |
| [3] |
Capasso V, Serio G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math Biosci, 1978, 42: 43-61
doi: 10.1016/0025-5564(78)90006-8 |
| [4] | Caraballo T, El Fatini M, Pettersson R, et al. A stochastic SIRI epidemic model with relapse and media coverage. Discrete Cont Dyn Sys B, 2018, 23(8): 3483-3501 |
| [5] |
Chen L H, Wei F Y. Persistence and distribution of a stochastic susceptible-infected-removed epidemic model with varying population size. Physica A, 2017, 483: 386-397
doi: 10.1016/j.physa.2017.04.114 |
| [6] | Chen L J, Wei F Y. Study on a susceptible-exposed-infected-recovered model with nonlinear incidence rate. Adv Differ Equ, 2020, Article number 206 |
| [7] |
Cui J G, Sun Y H, Zhu H P. The impact of media on the control of infectious diseases. J Dyn Differ Equ, 2008, 20(1): 31-53
doi: 10.1007/s10884-007-9075-0 pmid: 32214759 |
| [8] | Feng T, Meng X Z, Zhang T H, et al. Analysis of the predator-prey interactions: A stochastic model incorporating disease invasion. Qual Theory Dyn Sys, 2020, 19: Article number 55 |
| [9] | Guo Q, Liu W, Mao X R, et al. The partially truncated Euler-Maruyama method and its stability and boundedness. Appl Numer Math, 2017, 115: 235-251 |
| [10] |
Guo W J, Zhang Q M, Li X N, et al. Dynamic behavior of a stochastic SIRS epidemic model with media coverage. Math Method Appl Sci 2018, 41(14): 5506-5525
doi: 10.1002/mma.v41.14 |
| [11] |
Han B T, Jiang D Q, Zhou B Q, et al. Stationary distribution and probability density function of a stochastic SIRSI epidemic model with saturation incidence rate and logistic growth. Chaos, Solitons Fractals, 2011, 142: 110519
doi: 10.1016/j.chaos.2020.110519 |
| [12] |
Higham D J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev, 2001, 43: 525-546
doi: 10.1137/S0036144500378302 |
| [13] |
Hou T F, Lan G J, Yuan S L, et al. Threshold dynamics of a stochastic SIHR epidemic model of COVID-19 with general population-size dependent contact rate. Math Biosci Eng, 2022, 19: 4217-4236
doi: 10.3934/mbe.2022195 pmid: 35341295 |
| [14] |
Lan G J, Yuan S L, Song B J. The impact of hospital resources and environmental perturbations to the dynamics of SIRS model. J Frankl Inst-Eng Appl Math, 2021, 358(4): 2405-2433
doi: 10.1016/j.jfranklin.2021.01.015 |
| [15] |
Li J H, Teng Z D, Wang G Q, et al. Stability and bifurcation analysis of an SIR epidemic model with logistic growth and saturated treatment. Chaos Solitons Fractals, 2017, 99: 63-71
doi: 10.1016/j.chaos.2017.03.047 |
| [16] |
Li Y F, Cui J G. The effect of constant and pulse vaccination on SIS epidemic models incorporating media coverage. Commun Nonlinear Sci Numer Simul, 2019, 14(5): 2353-2365
doi: 10.1016/j.cnsns.2008.06.024 |
| [17] | Liu J M, Chen L J, Wei F Y. The persistence and extinction of a stochastic SIS epidemic model with Logistic growth. Adv Differ Equ, 2018, Article number 68 |
| [18] |
Liu Q, Jiang D Q, Hayat T, et al. Dynamical behavior of a higher order stochastically perturbed SIRI epidemic model with relapse and media coverage. Chaos Solitons Fractals, 2020, 139: 110013
doi: 10.1016/j.chaos.2020.110013 |
| [19] |
Liu Q, Jiang D Q, Hayat T, et al. Dynamics of a stochastic predator-prey model with stage structure for predator and Holling type II functional response. J Nonlinear Sci, 2018, 28: 1151-1187
doi: 10.1007/s00332-018-9444-3 |
| [20] | Liu Q, Jiang D Q, Shi N, et al. Dynamical behavior of a stochastic HBV infection model with logistic hepatocyte growth. Acta Math Sci, 2017, 37B(4): 927-940 |
| [21] |
Lu R X, Wei F Y. Persistence and extinction for an age-structured stochastic SVIR epidemic model with generalized nonlinear incidence rate. Physica A, 2019, 513: 572-587
doi: 10.1016/j.physa.2018.09.016 |
| [22] |
Mao X R, Wei F Y, Wiriyakraikul T. Positivity preserving truncated Euler-Maruyama method for stochastic Lotka-Volterra competition model. J Comput Appl Math, 2021, 394: 113566
doi: 10.1016/j.cam.2021.113566 |
| [23] | Mao X R. Stochastic Differential Equations and Applications. Chichester: Horwood Publishing, 2007 |
| [24] |
Mu X J, Zhang Q M, Rong L B. Optimal vaccination strategy for an SIRS model with imprecise parameters and Lèvy noise. J Frankl Inst-Eng Appl Math, 2019, 356(18): 11385-11413
doi: 10.1016/j.jfranklin.2019.03.043 |
| [25] |
Nguyen D H, Nguyen N N, Yin G. Stochastic functional Kolmogorov equations, I: Persistence. Stoch Process Appl, 2021, 142: 319-364
doi: 10.1016/j.spa.2021.09.007 |
| [26] |
Nguyen D H, Nguyen N N, Yin G. Stochastic functional Kolmogorov equations II: Extinction. J Differ Equ, 2021, 294(5): 1-39
doi: 10.1016/j.jde.2021.05.043 |
| [27] |
Nguyen D H, Yin G, Zhu C. Long-term analysis of a stochastic SIRS model with general incidence rates. SIAM J Appl Math, 2020, 80(2): 814-838
doi: 10.1137/19M1246973 |
| [28] |
Rajasekar S P, Pitchaimani M, Zhu Q X. Dynamic threshold probe of stochastic SIR model with saturated incidence rate and saturated treatment function. Physica A, 2019, 535: 122300
doi: 10.1016/j.physa.2019.122300 |
| [29] | Rajasekar S P, Pitchaimani M. Ergodic stationary distribution and extinction of a stochastic SIRS epidemic model with logistic growth and nonlinear incidence. Appl Math Comput, 2020, 377: 125143 |
| [30] |
Sahu G P, Dhar J. Analysis of an SVEIS epidemic model with partial temporary immunity and saturation incidence rate. Appl Math Model, 2012, 36(3): 908-923
doi: 10.1016/j.apm.2011.07.044 |
| [31] |
Sun C J, Yang W, Arino J, et al. Effect of media-induced social distancing on disease transmission in a two patch setting. Math Biosci, 2011, 230(2): 87-95
doi: 10.1016/j.mbs.2011.01.005 pmid: 21296092 |
| [32] | Tchuenche J M, Dube N, Bhunu C P, et al. The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health, 2011, 11(1): Article number S5 |
| [33] |
Wang L W, Liu Z J, Zhang X G. Global dynamics for an age-structured epidemic model with media impact and incomplete vaccination. Nonlinear Anal: Real World Appl, 2016, 32: 136-158
doi: 10.1016/j.nonrwa.2016.04.009 |
| [34] |
Wei F Y, Chen F X. Stochastic permanence of an SIQS epidemic model with saturated incidence and independent random perturbations. Physica A, 2016, 453: 99-107
doi: 10.1016/j.physa.2016.01.059 |
| [35] |
Wei F Y, Chen L H. Psychological effect on single-species population models in a polluted environment. Math Biosci, 2017, 290: 22-30
doi: S0025-5564(17)30142-6 pmid: 28583848 |
| [36] |
Wei F Y, Jiang H, Zhu Q X. Dynamical behaviors of a heroin population model with standard incidence rates between distinct patches. J Frankl Inst-Eng Appl Math, 2021, 358(9): 4994-5013
doi: 10.1016/j.jfranklin.2021.04.024 |
| [37] |
Wei F Y, Wang C J. Survival analysis of a single-species population model with fluctuations and migrations between patches. Appl Math Model, 2020, 81: 113-127
doi: 10.1016/j.apm.2019.12.023 |
| [38] |
Wei F Y, Xue R. Stability and extinction of SEIR epidemic models with generalized nonlinear incidence. Math Comput Simul, 2020, 170: 1-15
doi: 10.1016/j.matcom.2018.09.029 |
| [39] |
Zhang Y, Fan K G, Guo S J, et al. Ergodic stationary distribution of a stochastic SIRS epidemic model incorporating media coverage and saturated incidence rate. Physica A, 2019, 514: 671-685
doi: 10.1016/j.physa.2018.09.124 |
| [40] | Zhao Y N, Jiang D Q. Dynamics of stochastically perturbed SIS epidemic model with vaccination. Abstr Appl Anal, 2013, Article number 517439 |
| [41] | Zhao Y N, Jiang D Q. The threshold of a stochastic SIS epidemic model with vaccination. Appl Math Comput, 2014, 243: 718-727 |
| [42] |
Zhao Y, Zhang Y P, Yuan S L. The effect of media coverage on threshold dynamics for a stochastic SIS epidemic model. Physica A, 2018, 512: 248-260
doi: 10.1016/j.physa.2018.08.113 pmid: 32288106 |
| [1] | 赵彦军,孙晓辉,苏丽,李文轩. 具有Logistic增长和Beddington-DeAngelis发生率的随机SIRS传染病模型定性分析[J]. 数学物理学报, 2022, 42(6): 1861-1872. |
| [2] | 李江,蓝桂杰,张树文,魏春金. 一类随机葡萄糖-胰岛素模型动力学分析[J]. 数学物理学报, 2021, 41(6): 1937-1949. |
| [3] | 刘丽雅,蒋达清. 具有一般反应函数与贴壁生长现象的随机恒化器模型的全局动力学行为[J]. 数学物理学报, 2021, 41(6): 1912-1924. |
| [4] | 王腾飞,冯涛,孟新柱. 具有Crowley-Martin型功能反应的捕食者-食饵模型的复杂动力学和随机敏感性分析[J]. 数学物理学报, 2021, 41(4): 1192-1203. |
| [5] | 张仲华,张倩. 转换机制下具有非线性扰动的随机SIVS传染病模型的定性分析[J]. 数学物理学报, 2021, 41(4): 1218-1234. |
| [6] | 丰利香,王德芬. 具有隔离和不完全治疗的传染病模型的全局稳定性[J]. 数学物理学报, 2021, 41(4): 1235-1248. |
| [7] | 程欣欣,饶亚情,黄刚. 封闭空间中新型冠状病毒肺炎传播模型:以日本“钻石公主号”邮轮为例[J]. 数学物理学报, 2020, 40(2): 540-544. |
| [8] | 张鑫喆,贺国峰,黄刚. 一类具有接种和潜伏期的传染病模型及动力学分析[J]. 数学物理学报, 2019, 39(5): 1247-1259. |
| [9] | 韩祥临,汪维刚,莫嘉琪. 流行性病毒传播生态动力学系统[J]. 数学物理学报, 2019, 39(1): 200-208. |
| [10] | 李华,刘三红,方奕乐,张兴安. 儿童手足口病的数学建模和计算机模拟[J]. 数学物理学报, 2018, 38(5): 1032-1040. |
| [11] | 蓝桂杰,付盈洁,魏春金,张树文. 具有Holling Ⅲ功能性反应的随机捕食食饵模型的平稳分布和周期解[J]. 数学物理学报, 2018, 38(5): 984-1000. |
| [12] | 张丽萍, 赵瑜, 原三领. 一类具有非线性发生率的随机SIS传染病模型阈值动力学行为研究[J]. 数学物理学报, 2018, 38(1): 197-208. |
| [13] | 魏凤英, 林青腾. 一类具有校正隔离率随机SIQS模型的绝灭性与分布[J]. 数学物理学报, 2017, 37(6): 1148-1161. |
| [14] | 孟笑莹. 具有非单调发生率的时滞随机传染病模型分析[J]. 数学物理学报, 2017, 37(6): 1162-1175. |
| [15] | 郭庭光, 徐志庭. 带有扩散项和接种的传染病模型的行波解[J]. 数学物理学报, 2017, 37(6): 1129-1147. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 361
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 143
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|