数学物理学报 ›› 2023, Vol. 43 ›› Issue (5): 1607-1619.
计算自旋轨道耦合 Spin-2 BEC 基态的带拉格朗日乘子的正规梯度流法
- 计算与随机数学教育部重点实验室 & 湖南师范大学数学与统计学院 长沙 410081
-
收稿日期:2022-08-26修回日期:2023-03-23出版日期:2023-10-26发布日期:2023-08-09 -
作者简介:袁永军,Email:yyj1983@hunnu.edu.cn -
基金资助:国家自然科学基金(11971007)
A Normalized Gradient Flow with Lagrange Multipliers for Computing Ground States of Spin-Orbit Coupled Spin-2 Bose-Einstein Condensates
- LCSM (MOE) & School of Mathematics and Statistics, Hunan Normal University, Changsha 410081
-
Received:2022-08-26Revised:2023-03-23Online:2023-10-26Published:2023-08-09 -
Supported by:NSFC(11971007)
摘要:
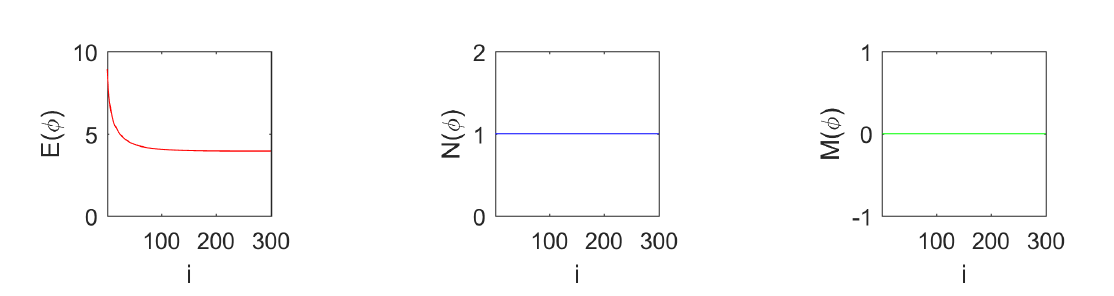
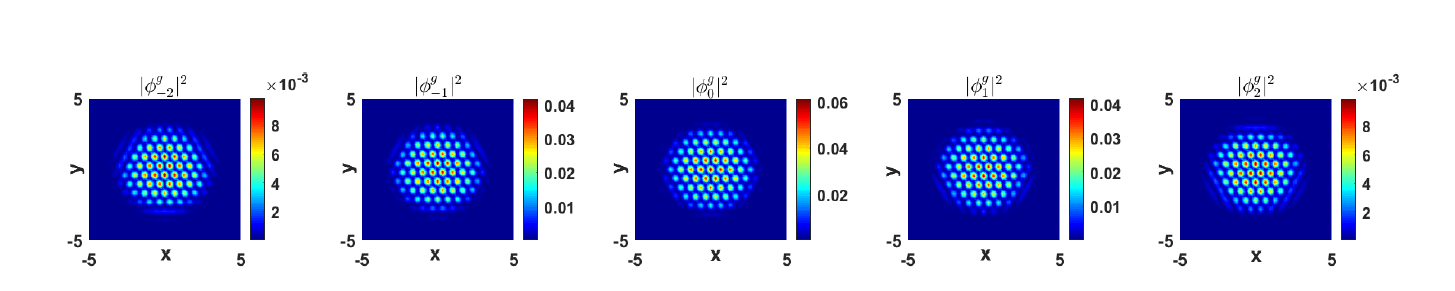
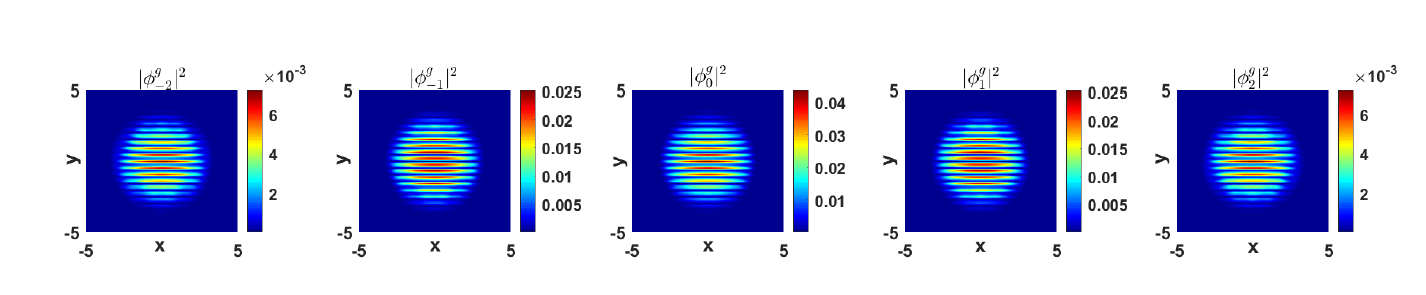
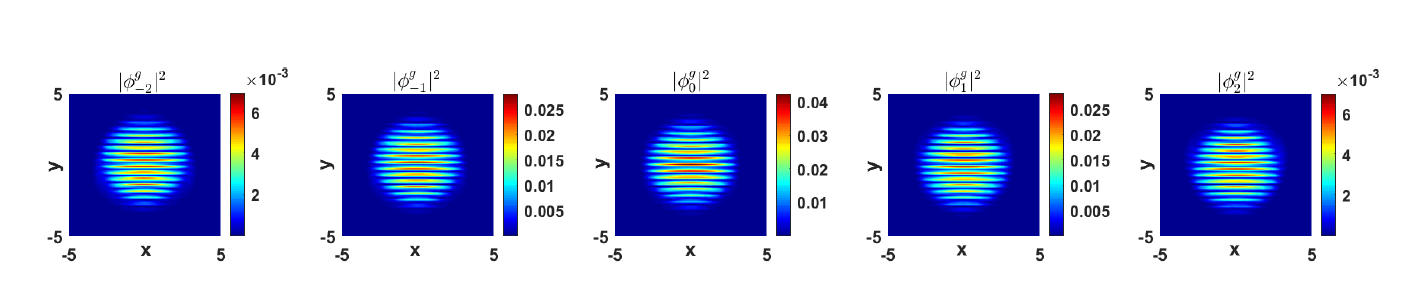
该文设计带拉格朗日乘子的正规梯度流法 (GFLM) 模拟自旋轨道耦合 Spin-2 玻色-爱因斯坦凝聚 (BEC) 的基态. 发掘投影系数间的隐含关系, 解决了模型中已有条件 (总质量及总磁场量守恒) 不足以确定所有投影系数的困难. 对循环型/铁磁体系下具有不同势函数的自旋轨道耦合 Spin-2 BEC 的基态进行了大量数值试验, 验证了算法的有效性, 并揭示了自旋轨道耦合 Spin-2 BEC 的条纹状基态与晶格状基态随自旋轨道耦合系数相互转化的相变规律.
中图分类号:
- O242.1
引用本文
袁永军. 计算自旋轨道耦合 Spin-2 BEC 基态的带拉格朗日乘子的正规梯度流法[J]. 数学物理学报, 2023, 43(5): 1607-1619.
Yuan Yongjun. A Normalized Gradient Flow with Lagrange Multipliers for Computing Ground States of Spin-Orbit Coupled Spin-2 Bose-Einstein Condensates[J]. Acta mathematica scientia,Series A, 2023, 43(5): 1607-1619.
使用本文
| [1] |
Anderson M H, Ensher J R, Matthewa M R, et al. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science, 1995, 269: 198-201
pmid: 17789847 |
| [2] | Antoine X, Levitt A, Tang Q. Efficient spectral computation of the stationary states of rotating Bose-Einstein condensates by preconditioned nonlinear conjugate gradient methods. Journal of Computational Physics, 2017, 343:92-109 |
| [3] | Bao W, Cai Y. Mathematical models and numerical methods for spinor Bose-Einstein condensates. Communications in Computational Physics, 2018, 24: 899-965 |
| [4] |
Bao W, Du Q. Computing the ground state solution of Bose-Einstein condensates by a normalized gradient flow. SIAM Journal on Scientific Computing, 2004, 25: 1674-1697
doi: 10.1137/S1064827503422956 |
| [5] |
Bao W, Lim F. Computing ground states of spin-1 Bose-Einstein condensates by the normalized gradient flow. SIAM Journal on Scientific Computing, 2008, 30 1925-1948
doi: 10.1137/070698488 |
| [6] |
Bao W, Tang W. Ground state solution of Bose-Einstein condensate by directly minimizing the energy functional. Journal of Computational Physics, 2003, 187: 230-254
doi: 10.1016/S0021-9991(03)00097-4 |
| [7] |
Bao W, Wang H. A mass and magnetization conservervative and energy-diminishing numerical method for computing ground state of spin-1 Bose-Einstein condensates. SIAM Journal on Numerical Analysis, 2007, 45(5): 2177-2200
doi: 10.1137/070681624 |
| [8] |
Bao W, Wang H, Markowich P A. Ground, symmetric and central vortex states in rotating Bose-Einstein condensates. Communications in Mathematical Sciences, 2005, 3(1): 57-88
doi: 10.4310/CMS.2005.v3.n1.a5 |
| [9] |
Bose. Plancks gesetz und lichtquantenhypothese. Zeitschrift fur Physik, 1924, 26: 178-181
doi: 10.1007/BF01327326 |
| [10] | Bradley C C, Sackett C A, Tollett J J, Hulet R G. Evidence of Bose-Einstein condensation in an atomic gas with attractive interaction. Physical Review Letters, 1995, 75: 1687-1690 |
| [11] |
Cai Y, Liu W. Efficient and accurate gradient flow methods for computing ground states of spinor Bose-Einstein condensates. Journal of Computational Physics, 2021, 433: 110183
doi: 10.1016/j.jcp.2021.110183 |
| [12] |
Davis K B, Mewes M O, Andrews M R, et al. Bose-Einstein condensation in a gas of sodium atoms. Physical Review Letters, 1995, 75: 3969-3973
pmid: 10059782 |
| [13] | Einstein A. Quantentheorie des einatomigen idealen gases. Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1924, 22: 261-267 |
| [14] | Einstein A. Quantentheorie des einatomigen idealen gases, zweite abhandlung. Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1925, 1: 3-14 |
| [15] |
Ho T L. Spinor Bose condensates in optical traps. Physical Review Letters, 1998, 81: 742-745
doi: 10.1103/PhysRevLett.81.742 |
| [16] |
Kawaguchi Y, Ueda M. Spinor Bose-Einstein condensates. Physics Reports, 2012, 520: 253-381
doi: 10.1016/j.physrep.2012.07.005 |
| [17] |
Liu W, Cai Y. Normalized gradient flow with Lagrange multiplier for computing ground states of Bose-Einstein condensates. SIAM Journal on Scientific Computing, 2021, 43(1): B219-B242
doi: 10.1137/20M1328002 |
| [18] |
Lin Y J, Compton R L, Jimenez-Garcia K, et al. Synthetic magmetic fields for ultracold neutral stoms. Nature, 2009, 462: 628-632
doi: 10.1038/nature08609 |
| [19] |
Lin Y J, Compton R L, Perry A R, et al. Bose-Einstein condensates in a uniform light-induced vector potential. Physical Review Letters, 2009, 102: 130401
doi: 10.1103/PhysRevLett.102.130401 |
| [20] |
Lin Y J, Jimenez-Garcia K, Spielman I B. A spin-orbit-coupled Bose-Einstein condensates. Nature, 2011, 471: 83-86
doi: 10.1038/nature09887 |
| [21] |
Stamper-Kurn D M, Andrews M R, Chikkatur A P, et al. Optical confinement of a Bose-Einstein condensate. Physical Review Letters, 1998, 80: 2027-2030
doi: 10.1103/PhysRevLett.80.2027 |
| [22] |
Stamper-Kurn D M, Ueda M. Spinor Bose gases: Symmetries, magnetism, and quantum dynamics. Review of Modern Physics, 2013, 85: 1191-1244
doi: 10.1103/RevModPhys.85.1191 |
| [23] |
Yuan Y, Xu Z, Tang Q, Wang H. The numerical study of the ground states of spin-1 Bose-Einstein condensates with spin-orbit-coupling. East Asian Journal on Applied Mathematics, 2018, 8(3): 598-610
doi: 10.4208/eajam |
| [1] | 李易娴,张正杰. 一类与 Klein-Gordon-Maxwell 问题有关的方程组的基态解的存在性[J]. 数学物理学报, 2023, 43(3): 680-690. |
| [2] | 李德科, 王青选. 质量临界非齐次薛定谔方程在门槛值处的极限行为[J]. 数学物理学报, 2023, 43(1): 123-131. |
| [3] | 李安然,樊丹丹,魏重庆. 临界零质量Kirchhoff型方程的解及其渐近行为[J]. 数学物理学报, 2022, 42(6): 1729-1743. |
| [4] | 邵春晖,孙吉江,马世旺. 带有超二次位势无限格点上的基态行波解[J]. 数学物理学报, 2022, 42(5): 1451-1461. |
| [5] | 王亚男,滕凯民. 带Choquard项的拟线性薛定谔方程的基态解[J]. 数学物理学报, 2022, 42(3): 730-748. |
| [6] | 尚旭东,张吉慧. 一类非线性Choquard方程基态解的存在性[J]. 数学物理学报, 2022, 42(3): 749-759. |
| [7] | 吉蕾,廖家锋. 一类带临界指数的Kirchhoff型问题正基态解的存在性[J]. 数学物理学报, 2022, 42(2): 418-426. |
| [8] | 杨连峰,曾小雨. 拟相对论薛定谔方程基态解的存在性与爆破行为[J]. 数学物理学报, 2022, 42(1): 165-175. |
| [9] | 陈鹏. 一类反应扩散方程的Nehari-Pankov型基态解[J]. 数学物理学报, 2021, 41(5): 1347-1356. |
| [10] | 成艺群,滕凯民. 非线性临界Kirchhoff型问题的正基态解[J]. 数学物理学报, 2021, 41(3): 666-685. |
| [11] | 韩娅玲,向建林. 一类分数阶p-Laplace方程基态解的存在性及其渐进行为[J]. 数学物理学报, 2020, 40(6): 1622-1633. |
| [12] | 黄小梦,张贻民. 一类修正Gross-Pitaevskii方程基态解的存在性[J]. 数学物理学报, 2020, 40(4): 850-856. |
| [13] | 梅艳芳,王友军. 一类非线性Schrödinger方程三种类型的解[J]. 数学物理学报, 2019, 39(5): 1087-1093. |
| [14] | 方立婉,黄文念,汪敏庆. 临界情形下Schrödinger-Maxwell方程的基态解[J]. 数学物理学报, 2019, 39(3): 475-483. |
| [15] | 余纯, 万优艳. 含超线性项的广义Choquard-Pekar方程基态解的存在性[J]. 数学物理学报, 2018, 38(2): 276-283. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 281
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 90
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|