| [1] |
Bieberbach L.      und die authomorphen Funktionen. Math Ann, 1916, 77: 173-212 und die authomorphen Funktionen. Math Ann, 1916, 77: 173-212
doi: 10.1007/BF01456901
|
| [2] |
Bingham N H, Goldie C M, Teugels J L. Regular Variation, Encyclopedia Math Appl. Cambridge: Cambridge University Press, 1987
|
| [3] |
Caffarelli L. Interior     estimates for solutions of the Monge-Ampère equation. Ann Math, 1990, 131: 135-150 estimates for solutions of the Monge-Ampère equation. Ann Math, 1990, 131: 135-150
doi: 10.2307/1971510
|
| [4] |
Caffarelli L, Nirenberg L, Spruck J. The Dirichlet problem for nonlinear second-order elliptic equations I. Monge-Ampère equations. Comm Pure Appl Math, 1984, 37: 369-402
doi: 10.1002/cpa.3160370306
|
| [5] |
Cheng S Y, Yau S T. On the regularity of the Monge-Ampère equation   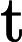                      . Comm Pure Appl Math, 1997, 30: 41-68 . Comm Pure Appl Math, 1997, 30: 41-68
doi: 10.1002/cpa.3160300104
|
| [6] |
Cheng S Y, Yau S T. On the existence of a complete Kähler metric on noncompact complex manifolds and the regularity of Fefferman's equation. Comm Pure Appl Math, 1980, 33: 507-544
doi: 10.1002/cpa.3160330404
|
| [7] |
Cheng S Y, Yau S T. The real Monge-Ampère equation and affine flat structures//Chern S S, Wu W. Proceedings of 1980 Beijing Symposium on Differential Geometry and Differential Equations, Vol 1. Beijing: Science Press, 1982: 339-370
|
| [8] |
Chuaqui M, Cortázar C, Elgueta M, Flores C, García-Melián J, Letelier R. On an elliptic problem with boundary blow-up and a singular weight: the radial case. Proc Roy Soc Edinburgh, 2003, 133: 1283-1297
doi: 10.1017/S0308210500002936
|
| [9] |
C  rstea F C, Trombetti C. On the Monge-Ampère equation with boundary blow-up: existence, uniqueness and asymptotics. Calc Var Partial Differential Equations, 2008, 31: 167-186 rstea F C, Trombetti C. On the Monge-Ampère equation with boundary blow-up: existence, uniqueness and asymptotics. Calc Var Partial Differential Equations, 2008, 31: 167-186
doi: 10.1007/s00526-007-0108-7
|
| [10] |
Du Y. Order Structure and Topological Methods in Nonlinear Partial Differential Equations. Singapore: World Scientific, 2006
|
| [11] |
García-Melián J. Boundary behavior for large solutions to elliptic equations with singular weights. Nonlinear Anal, 2007, 67: 818-826
doi: 10.1016/j.na.2006.06.041
|
| [12] |
Gladiali F, Porru G. Estimates for explosive solutions to  -Laplace equations, Progress in Partial Differential Equations (Pont-á-Mousson 1997), Vol 1. Pitman Res Notes Math Series, Longman, 1998, 383: 117-127 -Laplace equations, Progress in Partial Differential Equations (Pont-á-Mousson 1997), Vol 1. Pitman Res Notes Math Series, Longman, 1998, 383: 117-127
|
| [13] |
Guan B, Jian H. The Monge-Ampère equation with infinite boundary value. Pacific J Math, 2004, 216: 77-94
doi: 10.2140/pjm.2004.216.77
|
| [14] |
Jian H, Wang X, Zhao Y. Global smoothness for a singular Monge-Ampère equation. J Differential Equations, 2017, 263: 7250-7262
doi: 10.1016/j.jde.2017.08.004
|
| [15] |
Karamata J. Sur un mode de croissance régulière. Théorèmes fondamentaux. Bull Soc Math France, 1993, 61: 55-62
|
| [16] |
Keller J B. On solutions of        . Comm Pure Appl Math, 1957, 10: 503-510 . Comm Pure Appl Math, 1957, 10: 503-510
doi: 10.1002/cpa.3160100402
|
| [17] |
Lazer A C, McKenna P J. On singular boundary value problems for the Monge-Ampère operator. J Math Anal Appl, 1996, 197: 341-362
doi: 10.1006/jmaa.1996.0024
|
| [18] |
Matero J. The Bieberbach-Rademacher problem for the Monge-Ampère operator. Manuscripta Math, 1996, 91: 379-391
doi: 10.1007/BF02567962
|
| [19] |
Mohammed A. On the existence of solutions to the Monge-Ampère equation with infinite boundary values. Proc Amer Math Soc, 2007, 135: 141-149
doi: 10.1090/S0002-9939-06-08623-0
|
| [20] |
Mohammed A. Existence and estimates of solutions to a singular Dirichlet problem for the Monge-Ampère equation. J Math Anal Appl, 2008, 340: 1226-1234
doi: 10.1016/j.jmaa.2007.09.014
|
| [21] |
Olofsson A. Apriori estimates of Osserman-Keller type. Differ Integral Equ, 2003, 16: 737-756
|
| [22] |
Osserman R. On the inequality       . Pacific J Math, 1957, 7: 1641-1647 . Pacific J Math, 1957, 7: 1641-1647
doi: 10.2140/pjm.1957.7.1641
|
| [23] |
Pogorelov A V. The Multidimensional Minkowski Problem. New York: Wiley, 1978.
|
| [24] |
Rademacher H. Einige Besondere Probleme Partieller Differentialgleichungen, in: Die Differential- und Integralgleichungen, der Mechanik und Physikl. New York: Rosenberg, 1943
|
| [25] |
Savin O. Pointwise     estimates at the boundary for the Monge-Ampère equation. J Amer Math Soc, 2013, 26: 63-99 estimates at the boundary for the Monge-Ampère equation. J Amer Math Soc, 2013, 26: 63-99
doi: 10.1090/S0894-0347-2012-00747-4
|
| [26] |
Seneta E. Regular Varying Functions, Lecture Notes in Math. Heidelberg: Springer-Verlag, 1976
|
| [27] |
Trudinger N, Wang X. Boundary regularity for the Monge-Ampère and affine maximal surface equations. Ann Math, 2008, 167: 993-1028
doi: 10.4007/annals.2008.167.993
|
| [28] |
Tso K. On a real Monge-Ampère functional. Invent Math, 1990, 101: 425-448
doi: 10.1007/BF01231510
|
| [29] |
Wan H, Shi Y, Liu W. Refined second boundary behavior of the unique strictly convex solution to a singular Monge-Ampère equation. Adv Nonlinear Anal, 2022, 11: 321-356
|
| [30] |
Yang H, Chang Y. On the blow-up boundary solutions of the Monge-Ampère equation with singular weights. Commun Pure Appl Anal, 2012, 11: 697-708
|
| [31] |
Zhang X, Du Y. Sharp conditions for the existence of boundary blow-up solutions to the Monge-Ampère equation. Calc Var Partial Differential Equations, 2018, 57: 30
doi: 10.1007/s00526-018-1312-3
|
| [32] |
Zhang X, Feng M. Boundary blow-up solutions to the Monge-Ampère equation: Sharp conditions and asymptotic behavior. Adv Nonlinear Anal, 2020, 9: 729-744
|
| [33] |
Zhang X, Feng M. The existence and asymptotic behavior of boundary blow-up solutions to the  -Hessian equation. J Differential Equations, 2019, 267: 4626-4672 -Hessian equation. J Differential Equations, 2019, 267: 4626-4672
doi: 10.1016/j.jde.2019.05.004
|
| [34] |
Zhang Z. Optimal global and boundary behavior of large solutions to the Monge-Ampère equation. J Funct Anal, 2020, 278: 108512
doi: 10.1016/j.jfa.2020.108512
|
| [35] |
Zhang Z. Boundary behavior of large solutions to the Monge-Ampère equations with weights. J Differential Equations, 2015, 259: 2080-2100
doi: 10.1016/j.jde.2015.03.040
|
 ),Zhang Xuemei2(
),Zhang Xuemei2( )
)