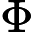| [1] |
Cianchi A, Maz'ya V. Global Lipschitz regularity for a class of quasilinear elliptic equations. Communications in Partial Differential Equations, 2011, 36(1): 100-133
doi: 10.1080/03605301003657843
|
| [2] |
Cianchi A, Maz'ya V. Global boundedness of the gradient for a class of nonlinear elliptic systems. Archive for Rational Mechanics and Analysis, 2014, 212(1): 129-177
doi: 10.1007/s00205-013-0705-x
|
| [3] |
Yao F P, Zhang C, Zhou S L. Global regularity estimates for a class of quasilinear elliptic equations in the whole space. Nonlinear Analysis, 2020, 194: 111307
doi: 10.1016/j.na.2018.07.004
|
| [4] |
Yao F P, Zhou S L. Calderón-Zygmund estimates for a class of quasilinear elliptic equations. Journal of Functional Analysis, 2017, 272(4): 1524-1552
doi: 10.1016/j.jfa.2016.11.008
|
| [5] |
Yao F P. Global Calderón-Zygmund estimates for a class of nonlinear elliptic equations with Neumann data. Journal of Mathematical Analysis and Applications, 2018, 457: 551-567
doi: 10.1016/j.jmaa.2017.08.030
|
| [6] |
DiBenedetto E, Manfredi J. On the higher integrability of the gradient of weak solutions of certain degenerate elliptic systems. American Journal of Mathematics, 1993, 115(5): 1107-1134
doi: 10.2307/2375066
|
| [7] |
Diening L, Kaplický P, Schwarzacher S. BMO estimates for the  -Laplacian. Nonlinear Analysis: Theory Methods and Applications, 2012, 75(2): 637-650 -Laplacian. Nonlinear Analysis: Theory Methods and Applications, 2012, 75(2): 637-650
|
| [8] |
Liang S, Zheng S Z. Gradient estimate in Orlicz spaces for elliptic obstacle problems with partially BMO nonlinearities. Electronic Journal of Differential Equations, 2018, 2018(58): 1-15
|
| [9] |
Acquistapace P. On BMO regularity for linear elliptic systems. Annali di Matematica Pura ed Applicata, 1992, 161: 231-269
doi: 10.1007/BF01759640
|
| [10] |
Danĕček J. The interior BMO-regularity for a weak solution of nonlinear second order elliptic systems. Nonlinear Differential Equations Applications, 2002, 9(4): 385-396
|
| [11] |
Yu H Y, Zheng S Z. BMO estimate to  -harmonic systems with discontinuous coefficients. Nonlinear Analysis: Real World Applications, 2015, 26: 64-74 -harmonic systems with discontinuous coefficients. Nonlinear Analysis: Real World Applications, 2015, 26: 64-74
doi: 10.1016/j.nonrwa.2015.05.003
|
| [12] |
张俊杰, 郑神州, 于海燕. 具有部分BMO系数的非散度型抛物方程的Lorentz估计. 数学物理学报, 2019, 39A(6): 1405-1420
|
|
Zhang J J, Zheng S Z, Yu H Y. Lorentz estimates for nondivergent parabolic equations with partial BMO coefficients. Acta Mathematica Scientia, 2019, 39A(6): 1405-1420
|
| [13] |
王支伟. 具有BMO系数的椭圆型方程在对数空间的正则性. 杭州: 浙江大学, 2012
|
|
Wang Z W. Regularity of Elliptic Equations with BMO Coefficients in Logarithmic Space. Hangzhou: Zhejiang University, 2012
|
| [14] |
佟玉霞, 王薪茹, 谷建涛. Orlicz空间中 -调和方程很弱解的 -调和方程很弱解的 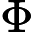 估计. 数学物理学报, 2020, 40A(6): 1461-1480 估计. 数学物理学报, 2020, 40A(6): 1461-1480
|
|
Tong Y X, Wang X R, Gu J T.  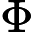 -type estimates for very weak solutions of -type estimates for very weak solutions of  -harmonic equation in Orlicz spaces. Acta Mathematica Scientia, 2020, 40A(6): 1461-1480 -harmonic equation in Orlicz spaces. Acta Mathematica Scientia, 2020, 40A(6): 1461-1480
|
| [15] |
张雅楠, 闫硕, 佟玉霞. 自然增长条件下的非齐次 -调和方程弱解的梯度估计. 数学物理学报, 2020, 40A(2): 379-394 -调和方程弱解的梯度估计. 数学物理学报, 2020, 40A(2): 379-394
|
|
Zhang Y N, Yan S, Tong Y X. Gradient estimates for weak solutions to non-homogeneous  -harmonic equations under natural growth. Acta Mathematica Scientia, 2020, 40A(2): 379-394 -harmonic equations under natural growth. Acta Mathematica Scientia, 2020, 40A(2): 379-394
|
| [16] |
Adams R A, Fournier J J F. Sobolev Spaces. New York: Academic Press, 2003
|
| [17] |
Diening L, Ettwein F. Fractional estimates for non-differentiable elliptic systems with general growth. Forum Mathematicum, 2008, 20(3): 523-556
|
| [18] |
Lieberman G M. The natural generalization of the natural conditions of Ladyzhenskaya and Ural'tseva for elliptic equations. Communications in Partial Differential Equations, 1991, 16(2): 311-361
doi: 10.1080/03605309108820761
|
 )
)