| 1 |
Šemrl P . Quadratic and Quasi-quadratic Functionals. Proc Amer Math Soc, 1993, 119 (4): 1105- 1113
doi: 10.1090/S0002-9939-1993-1158008-3
|
| 2 |
Huo D H , Zheng B D , Liu H Y . Nonlinear maps preserving Jordan triple  - - -products. J Math Anal Appl, 2015, 430 (2): 830- 844 -products. J Math Anal Appl, 2015, 430 (2): 830- 844
doi: 10.1016/j.jmaa.2015.05.021
|
| 3 |
Li C J , Zhao Y Y , Zhao F F . Nonlinear  -Jordan-type derivations on -Jordan-type derivations on  -algebras. Rochy MT J Math, 2021, 51 (2): 601- 612 -algebras. Rochy MT J Math, 2021, 51 (2): 601- 612
|
| 4 |
Taghavi A , Nouri M , Razeghi M , Darvish V . Non-linear  -Jordan triple -Jordan triple  -derivation on prime -derivation on prime  -algebras. Rochy MT J Math, 2018, 48 (8): 2705- 2716 -algebras. Rochy MT J Math, 2018, 48 (8): 2705- 2716
|
| 5 |
Li C J , Lu F Y , Fang X C . Non-linear  -Jordan -Jordan  -derivations on von Neumann algebras. Lin Multi Alg, 2014, 62 (4): 466- 473 -derivations on von Neumann algebras. Lin Multi Alg, 2014, 62 (4): 466- 473
doi: 10.1080/03081087.2013.780603
|
| 6 |
Zhang F J . Nonlinear skew Jordan derivable maps on factor von Neumann algebras. Lin Multi Alg, 2016, 64 (10): 2090- 2103
doi: 10.1080/03081087.2016.1139035
|
| 7 |
Zhao F F , Li C J . Nonlinear maps preserving the Jordan triple  -product between factors. Indagat Math, 2018, 29 (2): 619- 627 -product between factors. Indagat Math, 2018, 29 (2): 619- 627
doi: 10.1016/j.indag.2017.10.010
|
| 8 |
Li C J , Lu F Y . Nonlinear maps preserving the Jordan triple  - - -product on von Neumann algebras. Complex Anal Oper Th, 2017, 11 (1): 109- 117 -product on von Neumann algebras. Complex Anal Oper Th, 2017, 11 (1): 109- 117
doi: 10.1007/s11785-016-0575-y
|
| 9 |
Li C J , Chen Q Y , Wang T . Nonlinear maps preserving the Jordan triple  -product on factor von Neumann algebras. Chinese Ann Math B, 2018, 39 (4): 633- 642 -product on factor von Neumann algebras. Chinese Ann Math B, 2018, 39 (4): 633- 642
doi: 10.1007/s11401-018-0086-4
|
| 10 |
Li C J , Lu F Y , Wang T . Nonlinear maps preserving the Jordan triple  -product on von Neumann algebras. Ann Funct Anal, 2016, 7 (3): 496- 507 -product on von Neumann algebras. Ann Funct Anal, 2016, 7 (3): 496- 507
doi: 10.1215/20088752-3624940
|
| 11 |
张芳娟. 素 - 环上非线性保 - 环上非线性保       积. 数学学报, 2014, 57 (4): 775- 784 积. 数学学报, 2014, 57 (4): 775- 784
|
|
Zhang F J . Nonlinear preserving product        on prime on prime  -ring. Acta Math Sin, 2014, 57 (4): 775- 784 -ring. Acta Math Sin, 2014, 57 (4): 775- 784
|
| 12 |
张芳娟, 朱新宏. 因子von Neumann代数上的非线性 -Jordan -Jordan  - 三重可导映射. 数学物理学报, 2021, 41A (4): 978- 988 - 三重可导映射. 数学物理学报, 2021, 41A (4): 978- 988
doi: 10.3969/j.issn.1003-3998.2021.04.006
|
|
Zhang F J , Zhu X H . Nonlinear  -Jordan -Jordan  -triple derivable mappings on factor von Neumann algebras. Acta Math Sci, 2021, 41A (4): 978- 988 -triple derivable mappings on factor von Neumann algebras. Acta Math Sci, 2021, 41A (4): 978- 988
doi: 10.3969/j.issn.1003-3998.2021.04.006
|
| 13 |
Zhang F J , Qi X F , Zhang J H . Nonlinear  -Lie higher derivations on factor von Neumann algebras. B Iran Math Soc, 2016, 42 (3): 659- 678 -Lie higher derivations on factor von Neumann algebras. B Iran Math Soc, 2016, 42 (3): 659- 678
|
| 14 |
Huo D H , Zheng B D , Xu J L , Liu H Y . Nonlinear mappings preserving Jordan multiple  -product on factor von Neumann algebras. Lin Multi Alg, 2015, 63 (5): 1026- 1036 -product on factor von Neumann algebras. Lin Multi Alg, 2015, 63 (5): 1026- 1036
doi: 10.1080/03081087.2014.915321
|
| 15 |
霍东华, 刘红玉. 保持Jordan多重 - - - 积的非线性映射. 数学进展, 2021, 50 (2): 214- 230 - 积的非线性映射. 数学进展, 2021, 50 (2): 214- 230
|
|
Hou D H , Liu H Y . Nonlinear maps preserving Jordan multiple  - - -products. Advances in Mathematics, 2021, 50 (2): 214- 230 -products. Advances in Mathematics, 2021, 50 (2): 214- 230
|
| 16 |
杨丽春, 安润玲. von Neumann代数上的Lie可导映射. 数学物理学报, 2018, 38A (5): 864- 872
doi: 10.3969/j.issn.1003-3998.2018.05.004
|
|
Yang L C , An R L . Lie derivable maps on von Neumann algebras. Acta Math Sci, 2018, 38A (5): 864- 872
doi: 10.3969/j.issn.1003-3998.2018.05.004
|
| 17 |
齐霄霏. 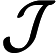 - 子空间格代数上中心化子和广义导子的刻画. 数学物理学报, 2014, 34A (2): 463- 472 - 子空间格代数上中心化子和广义导子的刻画. 数学物理学报, 2014, 34A (2): 463- 472
|
|
QI X F . Characterization of centralizers and generalized derivations on 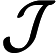 -subspace lattice algebras. Acta Math Sci, 2014, 34A (2): 463- 472 -subspace lattice algebras. Acta Math Sci, 2014, 34A (2): 463- 472
|
| 18 |
Zhang F J . Nonlinear  -Jordan triple -Jordan triple  -derivation on prime -derivation on prime  -algebras. Rochy MT J Math, 2022, 52 (1): 323- 333 -algebras. Rochy MT J Math, 2022, 52 (1): 323- 333
|
| 19 |
Zhang F J , Zhu X H . Nonlinear maps preserving the mixed triple products between factors. Journal of Mathematical Research with Applications, 2022, 42 (3): 297- 306
|
 ),Xinhong Zhu2
),Xinhong Zhu2