关于伪单调变分不等式与不动点问题的新投影算法

摘要/Abstract

摘要：

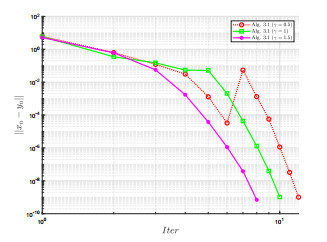
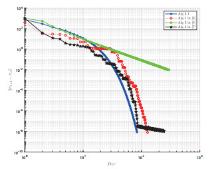
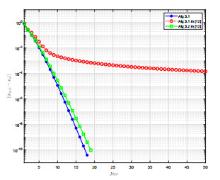
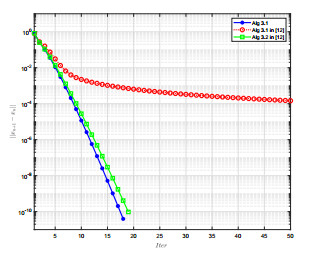
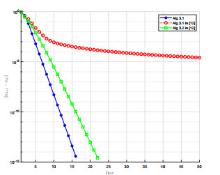
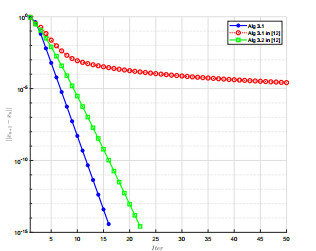
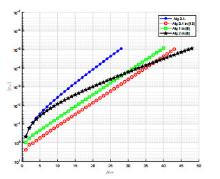
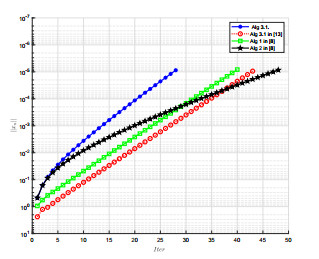
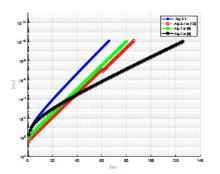
该文在Hilbert空间中给出了一个新投影算法，找到了伪单调变分不等式问题的解集与半压缩映射的不动点集的公共元.在映射是伪单调和一致连续的条件下，证明了强收敛定理.数值实验结果表明了新算法的有效性和优越性.

Abstract:

In this paper, we propose a new projection algorithm for finding a common element of psedomonotone variational inequality problems and fixed point set of demicontractive mappings in Hilbert spaces. We prove that this new algorithm converges strongly to the common element for a psedomonotone and uniformly continuous mapping. Finally, we provide some numerical experiments to illustrate the efficiency and advantages of the new projection algorithm.

Key words: Variational inequality, Fixed point, Projection algorithm, Uniformly continuous, Pseudomonotone

中图分类号:

O224

杨静,龙宪军. 关于伪单调变分不等式与不动点问题的新投影算法[J]. 数学物理学报, 2022, 42(3): 904-919.

Jing Yang,Xianjun Long. A New Projection Algorithm for Solving Pseudo-Monotone Variational Inequality and Fixed Point Problems[J]. Acta mathematica scientia,Series A, 2022, 42(3): 904-919.

图/表 12

图 1

图 2

表 1

图 3

图 4

表 2

图 5

图 6

表 3

图 7

图 8

表 4

参考文献 21

1	Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementarity Problems. New York: Springer, 2003
2	Kinderlehrer D, Stampacchia G. An Introduction to Variational Inequalities and Their Applications. New York: Academic Press, 1980
3	Goldstein A A . Convex programming in Hilbert space. Bull Amer Math Soc, 1964, 70, 709- 710 doi: 10.1090/S0002-9904-1964-11178-2
4	Tseng P . A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim, 2000, 38, 431- 446 doi: 10.1137/S0363012998338806
5	贺月红, 龙宪军. 求解伪单调变分不等式问题的惯性收缩投影算法. 数学物理学报, 2021, 41A(6): 1897-1911
	He Y H, Long X J. A inertial contraction and projection algorithm for pseudomonotone variational inequality problems. 2021, 41A(6): 1897-1911
6	万升联. 解变分不等式的一种二次投影算法. 数学物理学报, 2021, 41A(1): 237-244
	Wan S L. A double projection algorithm for solving variational inequalities. 2021, 41A(1): 237-244
7	Fan J J , Qin X L . Weak and strong convergence of inertial Tseng's extragradient algorithms for solving variational inequality problems. Optimization, 2021, 70, 1195- 1216 doi: 10.1080/02331934.2020.1789129
8	Thong D V , Voung P T . Modified Tseng's extragradient methods for solving pseudo-monotone variational inequalities. Optimization, 2019, 68, 2207- 2226 doi: 10.1080/02331934.2019.1616191
9	Yang J , Liu H W . Strong convergence result for solving monotone variational inequalities in Hilbert space. Numer Algor, 2019, 80, 741- 752 doi: 10.1007/s11075-018-0504-4
10	Lei M , He Y R . An extragradient method for solving variational inequalities without monotonocity. J Optim Theory Appl, 2021, 188, 432- 446 doi: 10.1007/s10957-020-01791-x
11	Thong D V , Hieu D V . Mann-type algorithms for variational inequality problems and fixed point problems. Optimization, 2020, 69, 2305- 2326 doi: 10.1080/02331934.2019.1692207
12	Thong D V , Hieu D V . Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems. Numer Algor, 2019, 82, 761- 789 doi: 10.1007/s11075-018-0626-8
13	郭丹妮, 蔡钢. 关于变分不等式和不动点问题的新迭代算法[OL]. 数学学报(中文版), [2021-01-15]. http://kns.cnki.net/kcms/detail/11.2038.O1.20210114.1040.010.html
	Guo D N, Cai G. A new iterative method for solving variational inequality and fixed point problems[OL]. Acta Mathematica Sinica(Chinese Series), [2021-01-15]. http://kns.cnki.net/kcms/detail/11.2038.O1.20210114.1040.010.html
14	Ceng L C , Shang M J . Hybrid inertial subgradient extragradient methods for variational inequalities and fixed point problems involving asymptotically nonexpansive mappings. Optimization, 2021, 70, 715- 740 doi: 10.1080/02331934.2019.1647203
15	Karamardian S . Complementarity problems over cones with monotone and pseudomonotone maps. J Optim Theory Appl, 1976, 18, 445- 454 doi: 10.1007/BF00932654
16	Chidume C E , Maruster S . Iterative methods for the computation of fixed points of demicontractive mappings. J Comput Appl Math, 2010, 234, 861- 882 doi: 10.1016/j.cam.2010.01.050
17	Goebel K, Reich S. Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. New York: Marcel Dekker, 1984
18	Denisov S V , Semenov V V , Chabak L M . Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators. Cybern Syst Anal, 2015, 51, 757- 765 doi: 10.1007/s10559-015-9768-z
19	Maingé P E . A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J Control Optim, 2008, 47, 1499- 1515 doi: 10.1137/060675319
20	Xu H K . Iterative algorithms for nonlinear operators. J Lond Math Soc, 2002, 66, 240- 256 doi: 10.1112/S0024610702003332
21	Cottle R W , Yao J C . Pseudo-monotone complementarity problems in Hilbert space. J Optim Theo Appl, 1992, 75, 281- 295 doi: 10.1007/BF00941468

$f(x)$	$m=30$		$m=60$		$m=90$
$f(x)$	Iter	CPU time	Iter	CPU time	Iter	GPU time
$\frac{x}{4}$	51	0.8511	52	0.7227	52	0.7869
$\frac{x}{2}$	53	0.7082	58	0.8453	62	0.9145
$\frac{\sin(x)}{2}$	55	0.7157	53	0.6831	57	0.9798
$\frac{\cos(x)}{2}$	236	5.7441	318	9.4689	427	19.516

$err=10^{-8}$	$m=50$		$m=60$		$m=70$
$err=10^{-8}$	Iter	CPU time	Iter	CPU time	Iter	CPU time
Alg 3.1	41	0.3043	42	0.3151	42	0.9606
Alg 1 in [8]	136	0.9405	145	0.9811	1902	38.337
Alg 2 in [8]	329	2.5770	490	3.7967	527	4.3241
Alg 4 in [7]	237	3.2041	533	9.0855	6513	106.62

$err$	Alg.3.1		Alg.3.2 in [12]		Alg.3.1 in [12]
$err$	Iter	CPU time	Iter	CPU time	Iter	GPU time
$10^{-10}$	12	0.0144	17	0.0239	24868	0.2387
$10^{-12}$	14	0.0154	19	0.0243	$\geq 10^{6}$	1.7069
$10^{-14}$	16	0.0165	22	0.0297	$\geq 10^{7}$	15.944

	$10^{-5}$		$10^{-10}$		$10^{-15}$
	Iter	CPU time	Iter	CPU time	Iter	GPU time
Alg 3.1	28	0.0138	66	0.0163	104	0.0529
Alg 1 in [8]	39	0.0238	80	0.0274	120	0.0635
Alg 2 in [8]	45	0.0257	126	0.0357	207	0.0933
Alg 3.1 in [13]	42	0.0142	86	0.0175	127	0.0548

[1]	杨蓝翔,陈艺,叶明露. 一类拟单调变分不等式的惯性投影算法[J]. 数学物理学报, 2023, 43(2): 593-603.
[2]	夏平静,蔡钢. Hilbert 空间中变分不等式问题的自适应粘性算法[J]. 数学物理学报, 2023, 43(2): 581-592.
[3]	徐家发, 杨志春. 高阶Riemann-Liouville型分数阶脉冲微分方程积分边值问题的正解[J]. 数学物理学报, 2023, 43(1): 53-68.
[4]	宋玉莹, 范虹霞. 一类中立型随机发展方程解的存在性与正则性[J]. 数学物理学报, 2023, 43(1): 238-248.
[5]	段洁, 夏福全. 求解变分不等式与不动点问题公共解的新Tseng型外梯度算法[J]. 数学物理学报, 2023, 43(1): 274-290.
[6]	施翠云,宾茂君. Banach空间中微分变分不等式系统的Bang-Bang准则[J]. 数学物理学报, 2022, 42(6): 1653-1670.
[7]	刘文杰,谢胜利. 脉冲无穷时滞中立型测度微分方程mild解的存在性[J]. 数学物理学报, 2022, 42(6): 1671-1681.
[8]	刘丽平,彭建文. 求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法[J]. 数学物理学报, 2022, 42(5): 1517-1536.
[9]	段磊,陈天兰. 带平均曲率算子的离散混合边值问题凸解的存在性[J]. 数学物理学报, 2022, 42(2): 379-386.
[10]	赵童,袁海龙,郭改慧. 一类具有修正的Leslie-Gower项的捕食-食饵模型的正解[J]. 数学物理学报, 2022, 42(1): 176-186.
[11]	韩晓玲,蔡蕙泽,杨虎军. 星图上非线性分数阶微分方程边值问题解的存在唯一性[J]. 数学物理学报, 2022, 42(1): 139-156.
[12]	贺月红,龙宪军. 求解伪单调变分不等式问题的惯性收缩投影算法[J]. 数学物理学报, 2021, 41(6): 1897-1911.
[13]	张纪凤,张伟,倪晋波,任丹丹. 带p(t)-Laplacian算子的分数阶Langevin方程反周期边值问题解的存在性[J]. 数学物理学报, 2021, 41(4): 1024-1032.
[14]	徐家发,罗洪林,刘立山. 一类具有p-Laplacian算子的分数阶差分方程边值问题的正解[J]. 数学物理学报, 2021, 41(2): 402-414.
[15]	梁载涛,单雪梦. $k $-Hessian方程径向解的存在性与多解性[J]. 数学物理学报, 2021, 41(1): 63-68.