非特征端点条件下PM函数的迭代根

数学物理学报 ›› 2022, Vol. 42 ›› Issue (2): 557-569.

非特征端点条件下PM函数的迭代根

唐肖¹,李林^2,*()

¹ 重庆师范大学数学科学学院重庆 401331
² 嘉兴学院数学系浙江嘉兴 314001

收稿日期:2021-02-01 出版日期:2022-04-26 发布日期:2022-04-18
通讯作者: 李林 E-mail:mathll@163.com
基金资助:
国家自然科学基金(12001537);国家自然科学基金(11671061);国家自然科学基金(12026207);浙江省自然科学基金(LY18A010017);重庆师范大学博士启动基金(20XLB033)

Characteristic Endpoints Question for Piecewise Monotone Functions

Xiao Tang¹,Lin Li^2,*()

¹ School of Mathematical Science, Chongqing Normal University, Chongqing 401331
² Faculty of Mathematics, Jiaxing University, Zhejiang Jiaxing 314001

Received:2021-02-01 Online:2022-04-26 Published:2022-04-18
Contact: Lin Li E-mail:mathll@163.com
Supported by:
the NSFC(12001537);the NSFC(11671061);the NSFC(12026207);the NSF of Zhejiang Province(LY18A010017);the PhD Start-up Fund of Chongqing Normal University(20XLB033)

摘要/Abstract

摘要：

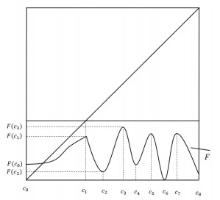
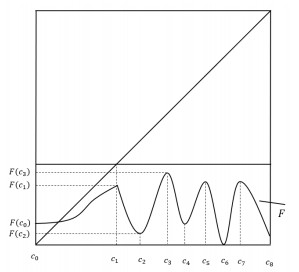
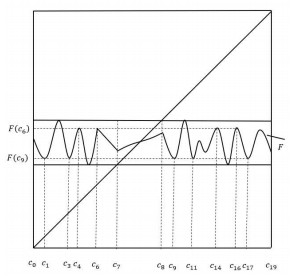
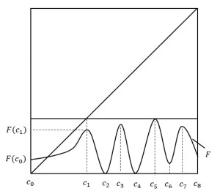
在特征端点条件下, 高度为1的PM函数的任意阶连续迭代根的存在性已经被证明.这就产生了一个在没有特征端点条件下的公开问题, 称为特征端点问题.当非单调点个数小于等于迭代根阶数时, 此问题在大部分情况下已解决.该文将研究非单调点个数大于迭代根阶数的情形, 给出高度为2且阶数也为2的连续迭代根存在的充分条件, 部分回答了特征端点问题.

关键词: 迭代根, 逐段单调函数, 特征区间, 特征端点条件

Abstract:

For PM functions of height 1, the existence of continuous iterative roots of any order was obtained under the characteristic endpoints condition. This raises an open problem about iterative roots without this condition, called characteristic endpoints problem. This problem is solved almost completely when the number of forts is equal to or less than the order. In this paper, we study the case that the number of forts is greater than the order and give a sufficient condition for existence of continuous iterative roots of order 2 with height 2, answering the characteristic endpoints problem partially.

Key words: Iterative root, Piecewise monotone function, Characteristic interval, Characteristic endpoints condition

中图分类号:

O175

唐肖,李林. 非特征端点条件下PM函数的迭代根[J]. 数学物理学报, 2022, 42(2): 557-569.

Xiao Tang,Lin Li. Characteristic Endpoints Question for Piecewise Monotone Functions[J]. Acta mathematica scientia,Series A, 2022, 42(2): 557-569.

图/表 4

表 1

图 1

图 2

图 3

参考文献 17

1	Babbage C . An Essay towards the calculus of functions. Philos Trans R Soc Lond, 1815, 105: 389- 423
2	Baron K , Jarczyk W . Recent results on functional equations in a single variable, perspectives and open problems. Aequationes Math, 2001, 61: 1- 48 doi: 10.1007/s000100050159
3	Fort M . The embedding of homeomorphisms in flows. Proc Amer Math Soc, 1955, 6: 960- 967 doi: 10.1090/S0002-9939-1955-0080911-2
4	Irwin M C . Smooth Dynamical Systems. New York: Academic Press, 1980
5	Kuczma M . On the functional equation $\varphi^n (x) = g(x)$. Ann Polon Math, 1961, 11: 161- 175 doi: 10.4064/ap-11-2-161-175
6	Kuczma M . Functional Equations in a Single Variable. Warszawa: Polish Scientific Publishers, 1968
7	Kuczma M , Choczewski B , Ger R . Iterative Functional Equations. Cambridge: Cambridge University Press, 1990
8	Li L , Chen J . Iterative roots of piecewise monotonic functions with finite nonmonotonicity height. J Math Anal Appl, 2014, 411: 395- 404 doi: 10.1016/j.jmaa.2013.09.051
9	Li L , Yang D L , Zhang W N . A note on iterative roots of PM functions. J Math Anal Appl, 2008, 341: 1482- 1486 doi: 10.1016/j.jmaa.2007.11.006
10	Li L , Zhang W N . The question on characteristic endpoints for iterative roots of PM functions. J Math Anal Appl, 2018, 458: 265- 280 doi: 10.1016/j.jmaa.2017.09.009
11	Liu L , Jarczyk W , Li L , Zhang W N . Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2. Nonlinear Anal, 2012, 75: 286- 303 doi: 10.1016/j.na.2011.08.033
12	Palis J , Melo W . Geometric Theory of Dynamical Systems: An Introduction. New York: Springer, 1982
13	Solarz P . General theorem for the existence of iterative roots of homeomorphisms with periodic points. J Math Anal Appl, 2012, 394: 391- 399 doi: 10.1016/j.jmaa.2012.03.048
14	Thompson J M T , Stewart H B . Nonlinear Dynamics and Chaos. Chichester: John Wiley & Sons, 1986
15	Zdun M , Solarz P . Recent results on iteration theory: iteration groups and semigroups in the real case. Aequationes Math, 2014, 87: 201- 245 doi: 10.1007/s00010-013-0186-x
16	张景中, 杨路. 论逐段单调连续函数的迭代根. 数学学报, 1983, 26 (4): 398- 412
17	Zhang W N . PM functions, their characteristic intervals and iterative roots. Ann Polon Math, 1997, 65: 119- 128 doi: 10.4064/ap-65-2-119-128

阶数	$ f $的性质	存在性或不存在性
$ n= 2 $	$ f $在$ [a', b'] $上$ \uparrow $, $ H(f)=1 $	不存在
	$ f $在$ [a', b'] $上$ \downarrow $, $ H(f)=1 $	存在
$ 2<n<N(F) $	$ f $在$ [a', b'] $上$ \uparrow $, $ H(f)<n $	不存在
	$ f $在$ [a', b'] $上$ \downarrow $, $ H(f)<n-1 $	不存在
$ n=N(F) $	$ f $在$ [a', b'] $上$ \uparrow $, $ H(f)\le n $	不存在
	$ f $在$ [a', b'] $上$ \downarrow $, $ H(f)<n-1 $	不存在
	$ f $在$ [a', b'] $上$ \downarrow $, $ H(f)=n $	存在
$ n=N(F)+1 $	$ f $在$ [a', b'] $上$ \uparrow $, $ H(f)\le n $	不存在
	$ f $在$ [a', b'] $上$ \downarrow $, $ H(f)<n-1 $	不存在

[1]	史诗洁,刘正荣,赵晖. 一类描述肿瘤入侵与具有信号依赖机制的趋化模型有界性与稳定性分析[J]. 数学物理学报, 2022, 42(2): 502-519.
[2]	程红梅,袁荣. 移动环境下带有非局部扩散项和时滞的反应扩散方程的强迫行波解[J]. 数学物理学报, 2022, 42(2): 491-501.
[3]	张伟强,赵培浩. 分数阶Choquard方程正解的存在性、多重性和集中现象[J]. 数学物理学报, 2022, 42(2): 470-490.
[4]	兰军. 一类二阶Duffing方程反周期解的存在性和多重性[J]. 数学物理学报, 2022, 42(2): 463-469.
[5]	姚绍文,李文洁,程志波. 三阶非线性微分方程周期解的非退化和存在唯一性[J]. 数学物理学报, 2022, 42(2): 454-462.
[6]	杜梦雪,李方卉,王征平. 含Hardy位势的非线性Schrödinger-Poisson方程正规化解的多重性[J]. 数学物理学报, 2022, 42(2): 442-453.
[7]	罗可欣,赖绍永. 一类高阶Camassa-Holm型方程整体弱解的存在性[J]. 数学物理学报, 2022, 42(2): 427-441.
[8]	胡蝶,高琦. 含有对数非线性项Kirchhoff方程多解的存在性[J]. 数学物理学报, 2022, 42(2): 401-417.
[9]	唐童,牛聪. 量子Navier-Stokes方程弱解的全局存在性[J]. 数学物理学报, 2022, 42(2): 387-400.
[10]	段磊,陈天兰. 带平均曲率算子的离散混合边值问题凸解的存在性[J]. 数学物理学报, 2022, 42(2): 379-386.
[11]	姜雪丽,邓璇,文邱浩,熊艳琴. 带两条平行切换直线多项式微分系统的极限环分支[J]. 数学物理学报, 2022, 42(2): 353-364.
[12]	张道祥, 李奔, 陈丹丹, 林雅婷, 王鑫梅. 带有经济效益的时滞分数阶微分-代数捕食-被捕食系统的Hopf分岔[J]. 数学物理学报, 2022, 42(2): 570-582.
[13]	王长有,李楠,蒋涛,杨强. 一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型[J]. 数学物理学报, 2022, 42(1): 245-268.
[14]	朱敏,刘梦丽. 一类具变系数交错扩散的登革热模型[J]. 数学物理学报, 2022, 42(1): 201-215.
[15]	赵童,袁海龙,郭改慧. 一类具有修正的Leslie-Gower项的捕食-食饵模型的正解[J]. 数学物理学报, 2022, 42(1): 176-186.