数学物理学报 ›› 2022, Vol. 42 ›› Issue (2): 570-582.
带有经济效益的时滞分数阶微分-代数捕食-被捕食系统的Hopf分岔
张道祥,李奔,陈丹丹,林雅婷,王鑫梅
- 安徽师范大学数学与统计学院 安徽芜湖 241002
-
收稿日期:2020-11-30出版日期:2022-04-26发布日期:2022-04-18 -
基金资助:国家自然科学基金(11671013);国家自然科学基金(11302002);安徽省自然科学基金(2008085MA13)
Hopf Bifurcation for a Fractional Differential-Algebraic Predator-Prey System with Time Delay and Economic Profit
Daoxiang Zhang,Ben Li,Dandan Chen,Yating Lin,Xinmei Wang
- School of Mathematics and Statistics, Anhui Normal University, Wuhu Anhui 241002
-
Received:2020-11-30Online:2022-04-26Published:2022-04-18 -
Supported by:the NSFC(11671013);the NSFC(11302002);the NSF of Anhui Province(2008085MA13)
摘要：
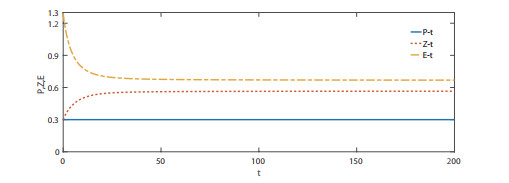
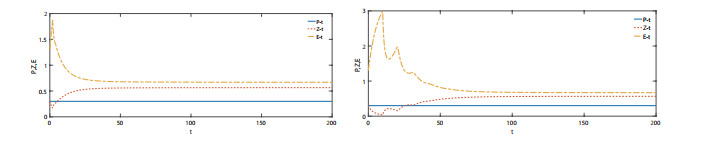
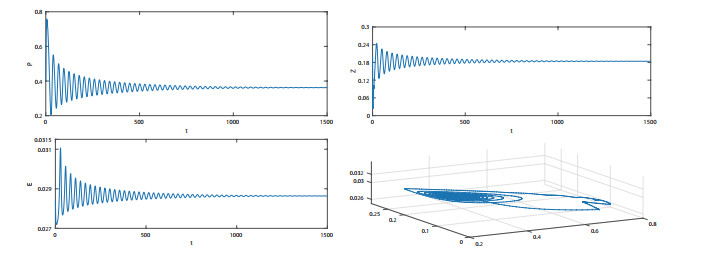
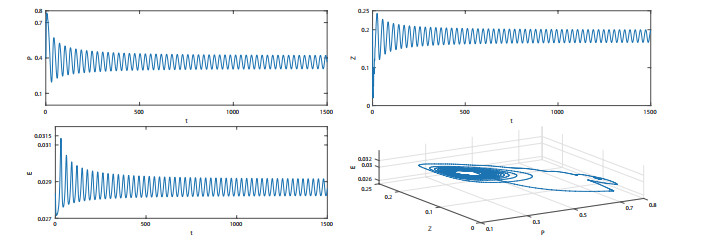
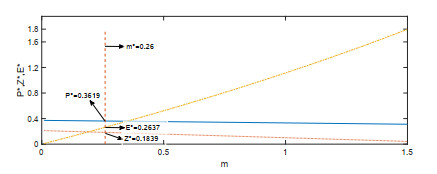
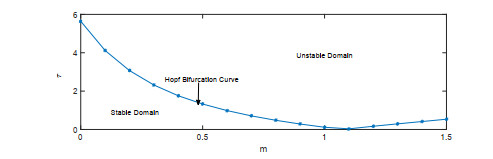
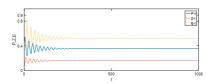
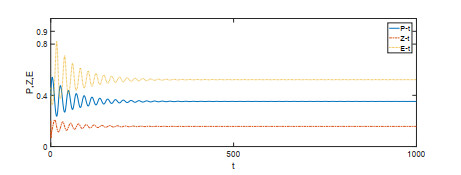
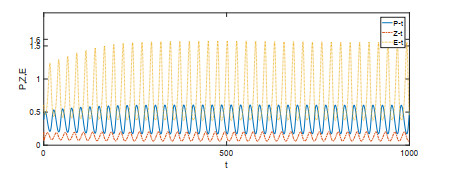
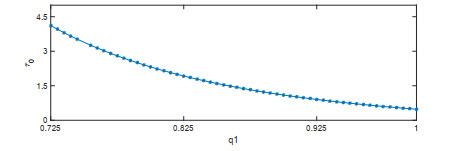
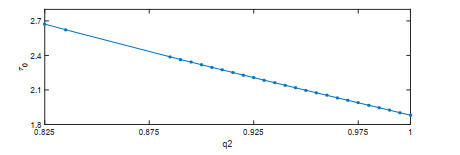
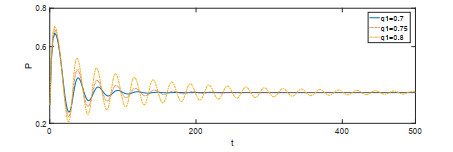
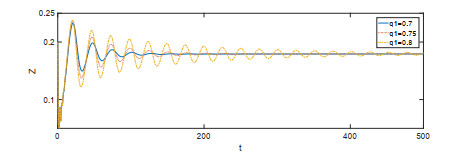
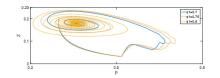
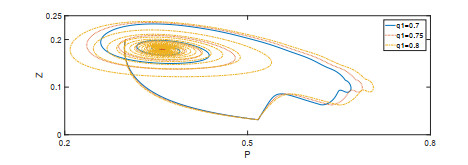
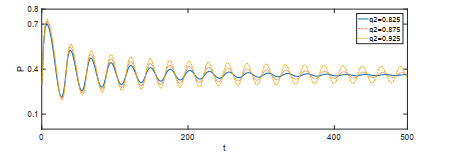
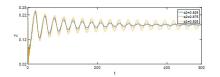
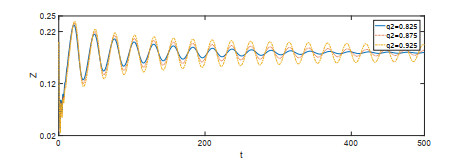
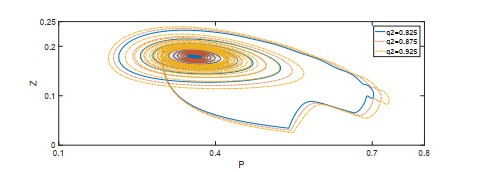
该文首先提出了一类带有经济效益的时滞分数阶微分-代数捕食-被捕食系统. 利用稳定性理论, 得到了在零经济收益条件下, 系统的正平衡点是局部渐近稳定的; 在正经济收益条件下, 时滞产生Hopf分岔的充分条件. 最后借助于数值模拟验证了理论的正确性, 并进一步讨论了分数阶阶数、经济收益和时滞对系统稳定性的影响.
中图分类号:
- O175.1
引用本文
张道祥,李奔,陈丹丹,林雅婷,王鑫梅. 带有经济效益的时滞分数阶微分-代数捕食-被捕食系统的Hopf分岔[J]. 数学物理学报, 2022, 42(2): 570-582.
Daoxiang Zhang,Ben Li,Dandan Chen,Yating Lin,Xinmei Wang. Hopf Bifurcation for a Fractional Differential-Algebraic Predator-Prey System with Time Delay and Economic Profit[J]. Acta mathematica scientia,Series A, 2022, 42(2): 570-582.
表 1
系统(1.1)相关变量和参数的意义"
| 变量(参数) | 意义 |
| 浮游植物的密度 | |
| 浮游动物的密度 | |
| 浮游植物种内干扰系数 | |
| 成熟捕食者的捕食率 | |
| 反应时间 | |
| 捕食者(浮游动物)之间的干扰程度 | |
| 喂食率 | |
| 转换效率 | |
| 浮游动物的死亡率 | |
| 时滞 | |
| Crowley-Martin[ |
表 1
图 1
$ \tau=0 $时系统(1.2)的积分曲线"
图 1
图 2
$ \tau = 2 $和$ \tau = 10 $时系统(1.2)的积分曲线"
图 2
图 3
系统(1.2)的积分曲线和相图. $ a = 1, b = 8, c = 3.9, d = 1.2, e = 0.0005, h = 1.1, $ $ g = 8, {p_1} = 10, {p_2} = 0.1, Q = 0.3, m = 0.26, q_1 = 0.8, q_2 = 0.9, \tau = 2.4 < {\tau _0} $"
图 3
图 4
系统(1.2)的积分曲线和相图. $ a = 1, b = 8, c = 3.9, d = 1.2, e = 0.0005, h = 1.1, $ $ g = 8, {p_1} = 10, {p_2} = 0.1, Q = 0.3, m = 0.26, q_1 = 0.8, q_2 = 0.9, \tau = 2.68 > {\tau _0} $"
图 4
图 5
$ m $与正平衡点$ {X^*} $的关系图"
图 5
图 6
稳定区域和不稳定区域随$ m $的增加而变化"
图 6
图 7
$ \tau=1, m = 0.5 $时, 系统(1.2)的积分曲线"
图 7
图 8
$ \tau=1, m = 0.65 $时, 系统(1.2)产生Hopf分岔"
图 8
图 9
$ q_1 $和$ {\tau _0} $的关系图"
图 9
图 10
$ q_2 $和$ {\tau _0} $的关系图"
图 10
图 11
$ {q_2} = 0.9, \tau = 2, q_1 = 0.7, 0.75, 0.8 $时系统(1.2)的积分曲线"
图 11
图 12
$ {q_2} = 0.9, \tau = 2, q_1 = 0.7, 0.75, 0.8 $时系统(1.2)的积分曲线"
图 12
图 13
$ {q_2} = 0.9, \tau = 2, q_1 = 0.7, 0.75, 0.8 $时系统(1.2)的相图"
图 13
图 14
$ {q_1} = 0.8, \tau = 2.2, q_2 = 0.825, 0.875, 0.925 $时系统(1.2)的积分曲线"
图 14
图 15
$ {q_1} = 0.8, \tau = 2.2, q_2 = 0.825, 0.875, 0.925 $时系统(1.2)的积分曲线"
图 15
图 16
$ {q_1} = 0.8, \tau = 2.2, q_2 = 0.825, 0.875, 0.925 $时系统(1.2)的相图"
图 16
| 1 |
Legendre L . The significance of microalgal blooms for fisheries and for the export of particulate organic carbon in oceans. Journal of Plankton Research, 1990, 12 (4): 681- 699
doi: 10.1093/plankt/12.4.681 |
| 2 | Liu X X , Huang Q D . The dynamics of a harvested predator-prey system with Holling type IV functional response. BioSystems, 2018, 169: 26- 39 |
| 3 |
Nosrati K , Shafiee M . Dynamic analysis of fractional-order singular Holling type-Ⅱ predator-prey system. Applied Mathematics and Computation, 2017, 313: 159- 179
doi: 10.1016/j.amc.2017.05.067 |
| 4 |
Scheffer M . Fish and nutrients interplay determines algal biomass: a minimal model. Oikos, 1991, 62: 271- 282
doi: 10.2307/3545491 |
| 5 |
Rihan F A , Anwar M N . Qualitative analysis of delayed SIR epidemic model with a saturated incidence rate. International Journal of Differential Equations, 2012,
doi: 10.1155/2012/408637 |
| 6 | Zhang D X , Sun G X , Zhao L X , Yan P . Pattern formation and selection in a diffusive predator-prey system with ratio-dependent functional response. Acta Ecologica Sinica, 2017, 38 (5): 290- 297 |
| 7 | Hillary R , Bees M . Plankton lattices and the role of chaos in plankton patchiness. Physical Review E, 2004, 69 (3): 1- 11 |
| 8 |
Han R J , Dai B X . Hopf bifurcation in a reaction-diffusive two-spcies model with nonlocal delay effect and general functional response. Chaos Solitons and Fractals, 2017, 96: 90- 109
doi: 10.1016/j.chaos.2016.12.022 |
| 9 | Rihan F A . Numerical modelling in biosciences using delay differential equations. Joural of Computational and Applied Mathematics, 2000, 125 (1/2): 183- 199 |
| 10 |
Zhang D X , Ding W W , Zhu M . Existence of positive periodic solutions of competitor-competitor-mutualist Lotka-Volterra systems with infinite delays. Journal of Systems Science and Complexity, 2015, 28 (2): 316- 326
doi: 10.1007/s11424-015-3128-y |
| 11 |
Rihan F A . Sensitivity analysis of dynamic systems with time lags. Joural of Computational and Applied Mathematics, 2003, 151 (2): 445- 462
doi: 10.1016/S0377-0427(02)00659-3 |
| 12 | Liao T C, Yu H G, Zhao M. Dynamics of delayed phytoplankton-zooplankton system with Crowley-Martin functional response. Advances in Difference Equations, 2017, 2017, Article number: 5 |
| 13 |
Crowley P H , Martin E K . Functional response and interference within and between year classes of a dragonfly population. Journal of the North American Benthological Society, 1989, 8 (3): 211- 221
doi: 10.2307/1467324 |
| 14 |
Zhao H Y , Zhang X B , Huang X X . Hopf bifurcation and spatial patterns of a delayed biological economic system with diffusion. Applied Mathematics and Computation, 2015, 266: 462- 480
doi: 10.1016/j.amc.2015.05.089 |
| 15 |
Battaglia J L , Cois O , Puigsegur L , Oustaloup A . Solving an inverse heat conduction problem using a non-integer identified model. International Journal of Heat and Mass Transf, 2001, 44 (14): 2671- 2680
doi: 10.1016/S0017-9310(00)00310-0 |
| 16 | Mainardi F. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics//Carpenteri A, Mainardi F. Fractals and Fractional Calculus in Continuum Mechanics. Wien: Springer, 1997: 291-348 |
| 17 | Hilfer R . Applications of Fractional Calculus in Physics. Singapore: World Scientific, 2000 |
| 18 |
Tlacuahuac A F , Biegler L T . Optimization of fractional order dynamic chemical processing systems. Industrial and Engineering Chemistry Research, 2014, 53 (13): 5110- 5127
doi: 10.1021/ie401317r |
| 19 |
Ahmed E , El-Sayed A M A , El-Saka H A . Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. Journal of Mathematical Analysis and Applications, 2007, 325 (1): 542- 553
doi: 10.1016/j.jmaa.2006.01.087 |
| 20 |
Huang C D , Li H , Cao J D . A novel strategy of bifurcation control for a delayed fractional predator-prey model. Applied Mathematics and Computation, 2019, 347: 808- 838
doi: 10.1016/j.amc.2018.11.031 |
| 21 | Abdelouahab M S , Hamri N E , Wang J . Hopf bifurcation and chaos in fractional-order modified hybrid optical system. Nonlinear Dynamics, 2011, 69 (1/2): 275- 284 |
| 22 |
Gutierrez-Vega J C . Fractionalization of optical beams: I. Planar analysis. Optics Letters, 2007, 32 (11): 1521- 1523
doi: 10.1364/OL.32.001521 |
| 23 |
Li H , Zhang L , Hu C . Dynamic analysis of a fractional-order single-species model with diffusion. Nonlinear Analysis: Modelling and Control, 2017, 22 (3): 303- 316
doi: 10.15388/NA.2017.3.2 |
| 24 |
Gordon H . The economic theory of a common property resource: The fishery. Journal of Political Economy, 1954, 62: 124- 142
doi: 10.1086/257497 |
| 25 |
Zhang X , Zhang Q , Zhang Y . Bifurcations of a class of singular biological economic models. Chaos Solitons and Fractals, 2009, 40 (3): 1309- 1318
doi: 10.1016/j.chaos.2007.09.010 |
| 26 |
Zhang X , Zhang Q Q . Bifurcation analysis and control of a differential-algebraic predator-prey model with Allee effect and time delay. Journal of Applied Mathematics, 2014,
doi: 10.1155/2014/107565 |
| 27 |
Zhang G , Zhu L , Chen B . Hopf bifurcation and stability for a differential-algebraic biological economic system. Applied Mathematics and Computation, 2010, 217 (1): 330- 338
doi: 10.1016/j.amc.2010.05.065 |
| 28 |
El-Saka H A A , Lee S , Jang B . Dynamic analysis of fractional-order predator-prey biological economic system with Holling type Ⅱ functional response. Nonlinear Dynamics, 2019, 96: 407- 416
doi: 10.1007/s11071-019-04796-y |
| 29 |
Nosrati K , Shafiee M . Dynamic analysis of fractional-order singular Holling type-Ⅱ predator-prey system. Applied Mathematics and Computation, 2017, 313: 159- 179
doi: 10.1016/j.amc.2017.05.067 |
| [1] | 程红梅,袁荣. 移动环境下带有非局部扩散项和时滞的反应扩散方程的强迫行波解[J]. 数学物理学报, 2022, 42(2): 491-501. |
| [2] | 朱凯旋,谢永钦,梅鑫钰,邓习军. 带有时滞项的超三次弱阻尼波方程一致吸引子的存在性[J]. 数学物理学报, 2022, 42(1): 86-102. |
| [3] | 王长有,李楠,蒋涛,杨强. 一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型[J]. 数学物理学报, 2022, 42(1): 245-268. |
| [4] | 孙悦,张道祥,周文. 恐惧效应对带时滞的反应扩散捕食系统的稳定区间的影响[J]. 数学物理学报, 2021, 41(6): 1980-1992. |
| [5] | 张再云,刘振海,邓又军. 具有时变时滞和速度相关材料密度的非线性粘弹性方程的整体存在性和一般衰减性[J]. 数学物理学报, 2021, 41(6): 1684-1704. |
| [6] | 仉志余,赵成,李宇宇. 时间尺度上带超线性中立项的二阶时滞动力方程的振动性[J]. 数学物理学报, 2021, 41(6): 1838-1852. |
| [7] | 覃桂茳,杨甲山. 具拟线性中立项的二阶变时滞动力方程的振动定理[J]. 数学物理学报, 2021, 41(5): 1492-1503. |
| [8] | 王晶囡,杨德中. 具时滞扩散效应的病原体-免疫模型的稳定性及分支[J]. 数学物理学报, 2021, 41(4): 1204-1217. |
| [9] | 仉志余. 具次线性中立项的二阶广义Emden-Fowler时滞微分方程的振动准则[J]. 数学物理学报, 2021, 41(3): 811-826. |
| [10] | 李喜玲,高飞,李文琴. 具有免疫时滞的分数阶HBV感染模型稳定性分析[J]. 数学物理学报, 2021, 41(2): 562-576. |
| [11] | 朱凯旋,谢永钦,周峰,邓习军. 带有时滞项的复Ginzburg-Landau方程的拉回吸引子[J]. 数学物理学报, 2020, 40(5): 1341-1353. |
| [12] | 刘健,张志信,蒋威. 分数阶非线性时滞脉冲微分系统的全局Mittag-Leffler稳定性[J]. 数学物理学报, 2020, 40(4): 1053-1060. |
| [13] | 黄星寿,罗日才,王五生. 基于Gronwall积分不等式的比例时滞神经网络稳定性分析[J]. 数学物理学报, 2020, 40(3): 824-832. |
| [14] | 阳超,李润洁. 一类具有不连续捕获的Lasota-Wazewska模型周期解存在性及稳定性分析[J]. 数学物理学报, 2019, 39(4): 785-796. |
| [15] | 周庆华,万立,刘杰. 具有变时滞的神经型Hopfield神经网络的全局吸引子研究[J]. 数学物理学报, 2019, 39(4): 823-831. |
|