一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型

数学物理学报 ›› 2022, Vol. 42 ›› Issue (1): 245-268.

一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型

王长有¹(),李楠^2,*(),蒋涛^3,^4,*(),杨强¹

¹ 成都信息工程大学应用数学学院成都 610225
² 西南财经大学应用数学学院成都 610074
³ 成都信息工程大学控制工程学院成都 610225
⁴ 中国科学院沈阳自动化研究所机器人国家重点实验室沈阳 110169

收稿日期:2020-09-26 出版日期:2022-02-26 发布日期:2022-02-23
通讯作者: 李楠,蒋涛 E-mail:wangchangyou417@163.com;2972028881@qq.com;jiangtop@126.com
作者简介:王长有, E-mail: wangchangyou417@163.com
基金资助:
机器人国家重点实验室研究基金(2019-O13);四川省科技厅科学研究项目(2021YFH0069);成都信息工程大学人才引进项目(KYTZ201820);四川省科技厅项目(21ZYZYTS0158)

On a Nonlinear Non-Autonomous Ratio-Dependent Food Chain Model with Delays and Feedback Controls

Changyou Wang¹(),Nan Li^2,*(),Tao Jiang^3,^4,*(),Qiang Yang¹

¹ College of Applied Mathematics, Chengdu University of Information Technology, Chengdu 610225
² Department of Applied Mathematics, Southwestern University of Finance and Economics, Chengdu 610074
³ Control Engineering College, Chengdu University of Information Technology, Chengdu 610225
⁴ State key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110169

Received:2020-09-26 Online:2022-02-26 Published:2022-02-23
Contact: Nan Li,Tao Jiang E-mail:wangchangyou417@163.com;2972028881@qq.com;jiangtop@126.com
Supported by:
the Robot Research Fund of State Key Laboratory(2019-O13);the Science Research Project of Sichuan Provincial Department(2021YFH0069);the Talent Introduction Project of Chengdu University of Information Engineering(KYTZ201820);the Sichuan Science and Technology Program(21ZYZYTS0158)

摘要/Abstract

摘要：

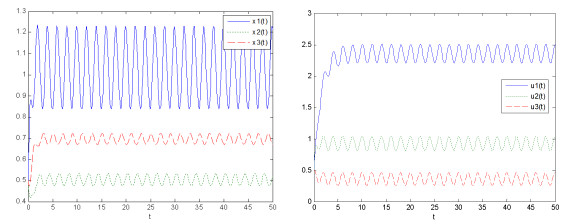
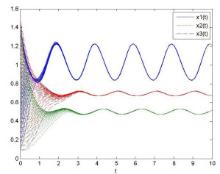
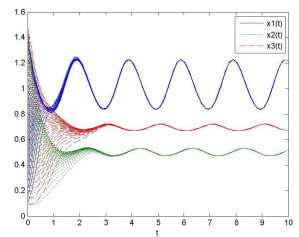
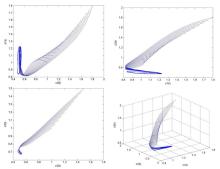
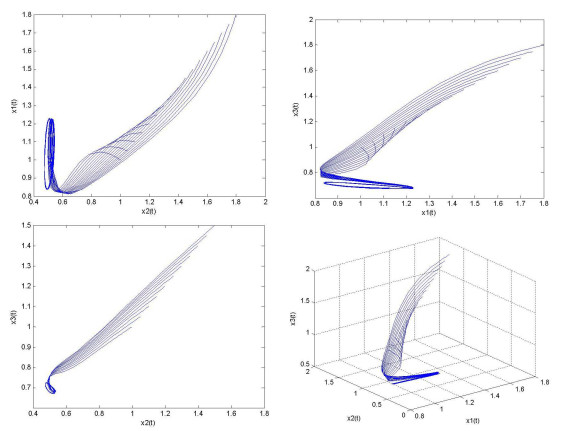
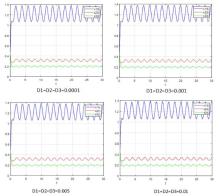
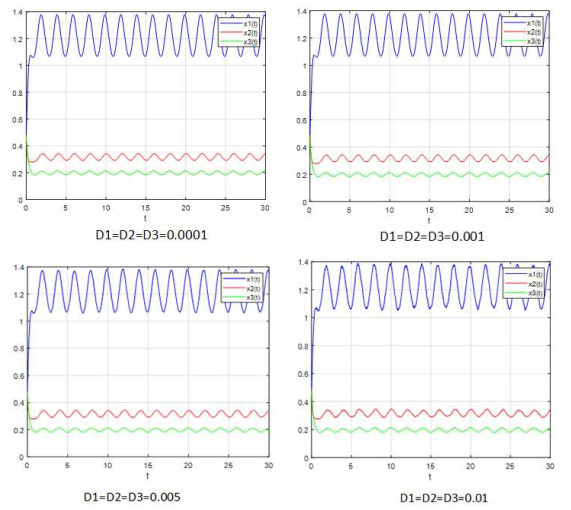
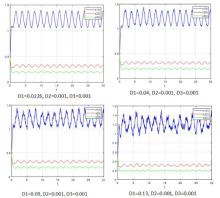
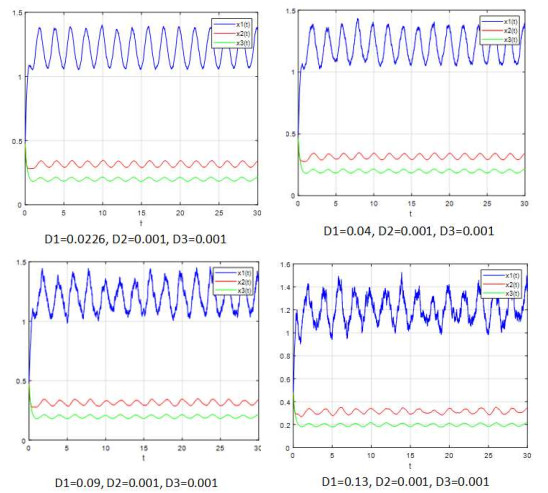
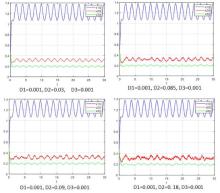
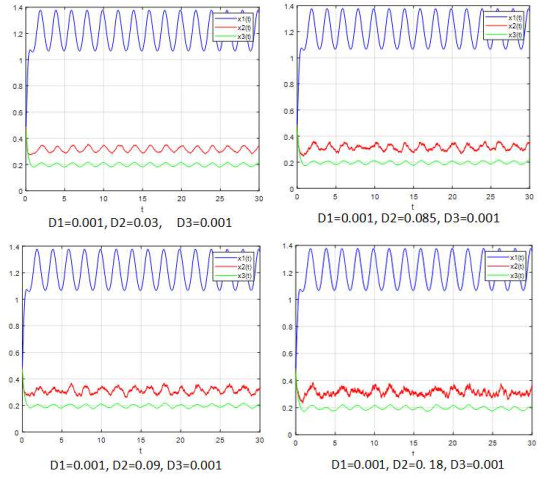
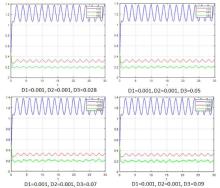
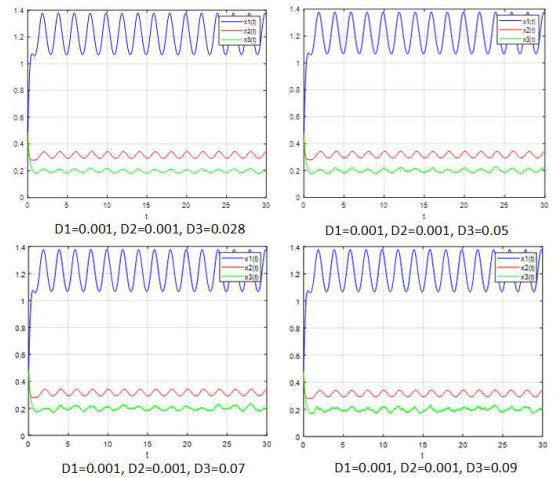
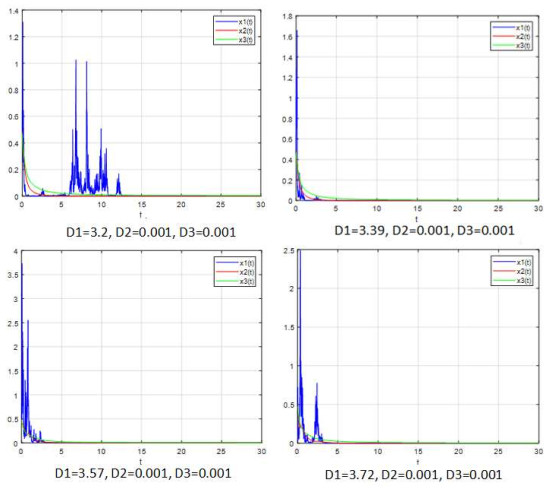
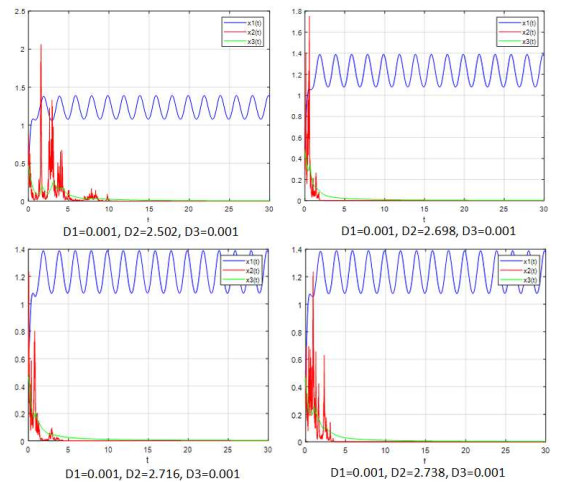
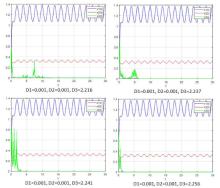
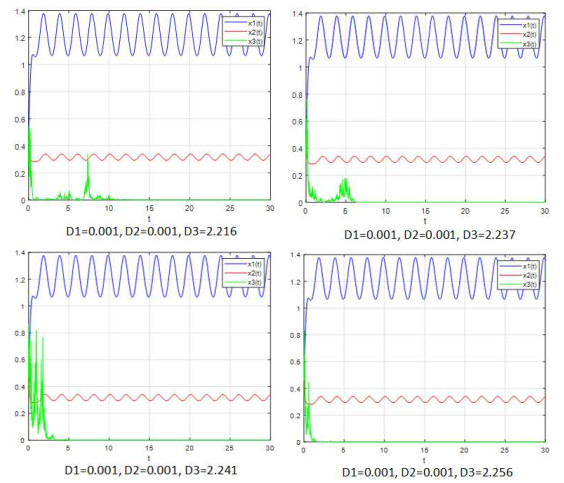
该文研究了一类具有时滞和反馈控制的三种群非线性非自治比率依赖的食物链模型.首先，基于时滞微分不等式理论，提出了一些新的分析方法，并构造了一个合适的李亚普诺夫函数.其次，得到了系统正解的持久性和全局吸引性的充分条件.第三，利用理论分析和不动点理论，讨论了相应的周期系统，建立了周期系统正周期解的存在性、唯一性和稳定性的充分条件.另外，给出了一些数值模拟，证明了我们的理论分析是正确的.最后，给出了相应的具有乘法噪声源的随机食物链模型的数值例子，并得到该模型一些新的有趣的解的变化过程.

关键词: 时滞, 比率依赖, 反馈控制, 持久性, 全局吸引性, 周期解

Abstract:

In this paper, we study a 3-species nonlinear non-autonomous ratio-dependent food chain system with delays and feedback controls. Firstly, based on the theory of delay differential inequality, some new analytical methods are developed and a suitable Lyapunov function is constructed. Secondly, sufficient conditions for the permanence and global attractivity of positive solutions for the system are obtained. Thirdly, by using the theoretical analysis and fixed point theory, the corresponding periodic systems are discussed, and the conditions for the existence, uniqueness and stability of positive periodic solutions of periodic systems are established. Moreover, we give some numerical simulations to prove that our theoretical analysis are correct. Finally, we still give an numerical example for the corresponding stochastic food chain model with multiplicative noise sources, and achieve new interesting change process of the solution for the model.

Key words: Delay, Ratio-Dependent, Feedback Control, Permanence, Global Attractive, Periodic solution

中图分类号:

O175.12

王长有,李楠,蒋涛,杨强. 一类具有时滞及反馈控制的非自治非线性比率依赖食物链模型[J]. 数学物理学报, 2022, 42(1): 245-268.

Changyou Wang,Nan Li,Tao Jiang,Qiang Yang. On a Nonlinear Non-Autonomous Ratio-Dependent Food Chain Model with Delays and Feedback Controls[J]. Acta mathematica scientia,Series A, 2022, 42(1): 245-268.

图/表 10

图 1

图 2

图 3

图 4

图 5

图 6

图 7

图 8

图 9

图 10

参考文献 38

1	Arditi R , Ginzburg L R . Coupling in predator-prey dynamics: Ratio-dependence. Journal of Theoretical Biology, 1989, 139 (3): 311- 326 doi: 10.1016/S0022-5193(89)80211-5
2	Basener W. Topology and Its Applications. Hoboken, NJ: John Wiley & Sons, 2006
3	Celik C . Stability and Hopf Bifurcation in a delayed ratio dependent Holling-Tanner type model. Applied Mathematics and Computation, 2015, 255: 228- 237 doi: 10.1016/j.amc.2014.11.086
4	Chen F . On a nonlinear nonautonomous predator-prey model with diffusion and distributed delay. Journal of Computational and Applied Mathematics, 2005, 180 (1): 33- 49 doi: 10.1016/j.cam.2004.10.001
5	Denaro G , Valenti D , La Cognata A , et al. Spatio-temporal behaviour of the deep chlorophyll maximum in Mediterranean Sea: Development of a stochastic model for picophytoplankton dynamics. Ecological Complexity, 2013, 13: 21- 34 doi: 10.1016/j.ecocom.2012.10.002
6	Ding W , Huang W Z . Global dynamics of a ratio-dependent holling-tanner predator-prey system. Journal of Mathematical Analysis and Applications, 2018, 460 (1): 458- 475 doi: 10.1016/j.jmaa.2017.11.057
7	Dubkov A A , Spagnolo B . Verhulst model with lévy white noise excitation. The European Physical Journal B, 2008, 65 (3): 361- 367 doi: 10.1140/epjb/e2008-00337-0
8	Falci G, La Cognata A, Berritta M, et al. Design of a lambda system for population transfer in superconducting nanocircuits. Physical Review B, 2013, 87, ID: 214515
9	Feistel R, Ebeling W. Evolution of Complex System. Dordrecht: Kluwer, 1989
10	Freeze M , Chang Y , Feng W . Analysis of dynamics in a complex food chain with ratio-dependent functional response. Journal of Applied Analysis & Computation, 2014, 4 (1): 69- 87
11	Garay J , Cressman R , Xu F , et al. Optimal forager against ideal free distributed prey. The American Naturalist, 2015, 186 (1): 111- 122 doi: 10.1086/681638
12	Giuffrida A , Valenti D , Ziino G , et al. A stochastic interspecific competition model to predict the behaviour of Listeria monocytogenes in the fermentation process of a traditional Sicilian salami. European Food Research and Technology, 2009, 228 (5): 767- 775 doi: 10.1007/s00217-008-0988-6
13	Gopalsamy K , Weng P . Global attractivity in a competition system with feedback controls. Computers and Mathematics with Applications, 2003, 45 (4/5): 665- 676
14	Haken H . Advanced Synergetics. Berlin: Springer, 1985
15	Horsthemke W , Lefever R . Noise-Induced Transitions. Theory and Applications in Physics. Chemistry, and Biology. Berlin: Springer, 1984
16	Khalil H K. Nonlinear Systems. Englewood Cliffs: Prentice-Hall, 2002
17	Liang Z Q , Pan H W . Qualitative analysis of a ratio-dependent holling-tanner model. Journal of Mathematical Analysis & Applications, 2007, 334 (2): 954- 964
18	Liang Z Q , Zeng X P , Pang G P , Liang Y H . Periodic solution of a leslie predator-prey system with ratio-dependent and state impulsive feedback control. Nonlinear Dynamics, 2017, 89 (4): 2941- 2955 doi: 10.1007/s11071-017-3637-4
19	Louartassi Y , Alla A , Hattaf K , Nabil A . Dynamics of a predator-prey model with harvesting and reserve area for prey in the presence of competition and toxicity. Journal of Applied Mathematics and Computing, 2019, 59 (1/2): 305- 321
20	Lu G , Lu Z , Lian X . Delay effect on the permanence for lotka-volterra cooperative systems. Nonlinear Analysis: Real World Applications, 2010, 11 (4): 2810- 2816 doi: 10.1016/j.nonrwa.2009.10.005
21	Mikhaylov A N , Gryaznov E G , Belov A L , et al. Field- and irradiation-induced phenomena in memristive nanomaterials. Physica Status Solidi (c), 2016, 13: 870- 881 doi: 10.1002/pssc.201600083
22	Muhammadhaji A , Teng Z , Rehim M . Dynamical behavior for a class of delayed competitive-mutualism systems. Differential Equations and Dynamical Systems, 2015, 23 (3): 281- 301 doi: 10.1007/s12591-014-0226-6
23	Nakata Y , Muroya Y . Permanence for nonautonomous Lotka-Volterra cooperative systems with delays. Nonlinear Analysis: Real World Applications, 2010, 11 (1): 528- 534 doi: 10.1016/j.nonrwa.2009.01.002
24	Nicolis G , Prigogine L . Self-Organization in Non-Equilibrium Systems. New Jersey: Wiley, 1977
25	Nie L , Teng Z , Hu L , Peng J G . Permanence and stability in non-autonomous predator-prey Lotka-Volterra systems with feedback controls. Computers & Mathematics with Applications, 2009, 58 (3): 436- 448
26	Shen C X , You M S . Permanence and extinction of a three-species ratio-dependent food chain model with delay and prey diffusion. Applied Mathematics and Computation, 2010, 217 (5): 1825- 1830 doi: 10.1016/j.amc.2010.02.037
27	Spagnolo B , La Barbera A . Role of the noise on the transient dynamics of an ecosystem of interacting species. Physica A: Statistical Mechanics and its Applications, 2002, 315 (1/2): 114- 124
28	Spagnolo B , Dubkov A A , Pankratov A L , et al. Lifetime of metastable states and suppression of noise in interdisciplinary physical models. Acta Physica Polonica B, 2007, 38 (5): 1925- 1950
29	Spagnolo B , Valenti D . Volatility effects on the escape time in financial market models. International Journal of Bifurcation and Chaos, 2008, 18 (9): 2775- 2786 doi: 10.1142/S0218127408022007
30	Valenti D , Schimansky-Geier L , Sailer X , Spagnolo B . Moment equations for a spatially extended system of two competing species. The European Physical Journal B, 2006, 50 (1/2): 199- 203
31	Wang C Y , Li N , Zhou Y , Pu X , Li R . On a multi-delay lotka-volterra predator-prey model with feedback controls and prey diffusion. Acta Mathematica Scientia, 2019, 39B (2): 429- 448
32	Wang C Y, Zhou Y Q, Li Y H, Li R. Well-posedness of a ratio-dependent lotka-volterra system with feedback control. Boundary Value Problems, 2018, 2018, ID: 117
33	Xu F , Cressman R , Křivan V . Evolution of mobility in predator-prey systems. Discrete and Continuous Dynamical Systems-Series B, 2014, 19 (10): 3397- 3432 doi: 10.3934/dcdsb.2014.19.3397
34	Xu J, Chen F. Permanence of a Lotka-Volterra cooperative system with time delays and feedback controls. Communications in Mathematical Biology & Neuroscience, 2015, 2015, ID: 18
35	Xu R , Chaplain M . Persistence and global stability in a delayed predator-prey system with michaelis-menten type functional response. Applied Mathematics and Computation, 2002, 130 (1): 441- 455
36	Xu R , Chen L S . Ersistence and global stability for a delayed nonautonomous predator-prey system without dominating instantaneous negative feedback. Journal of Mathematical Analysis and Applications, 2001, 262 (1): 50- 61 doi: 10.1006/jmaa.2001.7524
37	Zhou J , Mu C . Coexistence of a diffusive predator-prey model with holling type-Ⅱ functional response and density dependent mortality. Journal of Mathematical Analysis and Applications, 2012, 385 (2): 913- 927 doi: 10.1016/j.jmaa.2011.07.027
38	Zhang Q M, Zhang X J, Yang H F. Global dissipativity of stochastic Lotka-Volterra system with feedback controls. International Journal of Biomathematics, 2017, 10(2), ID: 1750022

[1]	朱凯旋, 谢永钦, 梅鑫钰, 邓习军. 带有时滞项的超三次弱阻尼波方程一致吸引子的存在性[J]. 数学物理学报, 2022, 42(1): 86-102.
[2]	杨瑜. 一类非局部时滞的SVIR反应扩散模型的全局吸引性[J]. 数学物理学报, 2021, 41(6): 1864-1870.
[3]	孙悦,张道祥,周文. 恐惧效应对带时滞的反应扩散捕食系统的稳定区间的影响[J]. 数学物理学报, 2021, 41(6): 1980-1992.
[4]	张再云,刘振海,邓又军. 具有时变时滞和速度相关材料密度的非线性粘弹性方程的整体存在性和一般衰减性[J]. 数学物理学报, 2021, 41(6): 1684-1704.
[5]	仉志余,赵成,李宇宇. 时间尺度上带超线性中立项的二阶时滞动力方程的振动性[J]. 数学物理学报, 2021, 41(6): 1838-1852.
[6]	覃桂茳,杨甲山. 具拟线性中立项的二阶变时滞动力方程的振动定理[J]. 数学物理学报, 2021, 41(5): 1492-1503.
[7]	杨静,柯昌成,魏周超. 一类连续和不连续分段线性系统的周期解研究[J]. 数学物理学报, 2021, 41(4): 1053-1065.
[8]	王晶囡,杨德中. 具时滞扩散效应的病原体-免疫模型的稳定性及分支[J]. 数学物理学报, 2021, 41(4): 1204-1217.
[9]	张清业,徐斌. 一类带局部非线性项的静态狄拉克方程的多重周期解[J]. 数学物理学报, 2021, 41(4): 1013-1023.
[10]	仉志余. 具次线性中立项的二阶广义Emden-Fowler时滞微分方程的振动准则[J]. 数学物理学报, 2021, 41(3): 811-826.
[11]	鲁世平,周诗乐,余星辰. 具有不确定奇性的Liénard方程周期正解的存在性[J]. 数学物理学报, 2021, 41(3): 686-701.
[12]	李喜玲,高飞,李文琴. 具有免疫时滞的分数阶HBV感染模型稳定性分析[J]. 数学物理学报, 2021, 41(2): 562-576.
[13]	蒋婷婷,杜增吉. 带有脉冲和Holling-IV型功能反应函数的中立型捕食-食饵模型的周期解[J]. 数学物理学报, 2021, 41(1): 178-193.
[14]	朱凯旋,谢永钦,周峰,邓习军. 带有时滞项的复Ginzburg-Landau方程的拉回吸引子[J]. 数学物理学报, 2020, 40(5): 1341-1353.
[15]	刘健,张志信,蒋威. 分数阶非线性时滞脉冲微分系统的全局Mittag-Leffler稳定性[J]. 数学物理学报, 2020, 40(4): 1053-1060.