具有年龄等级结构的种群竞争系统的最优收获控制

摘要/Abstract

摘要：

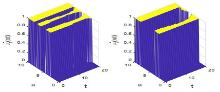
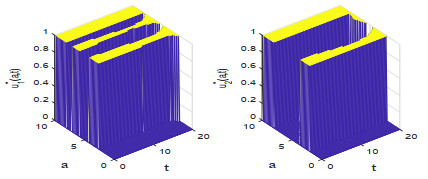
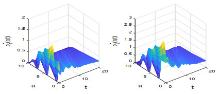
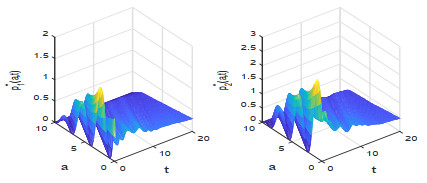
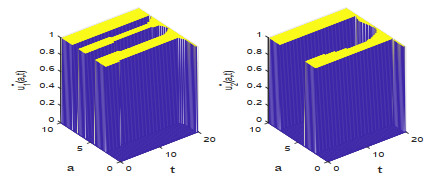
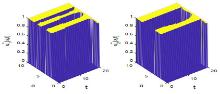
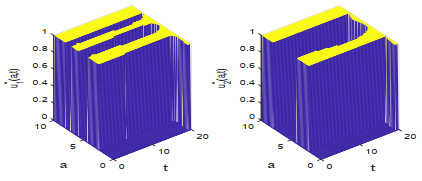
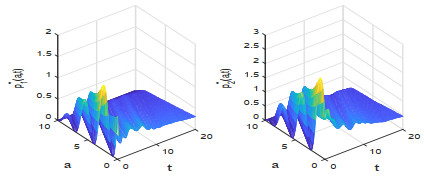
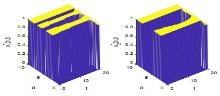
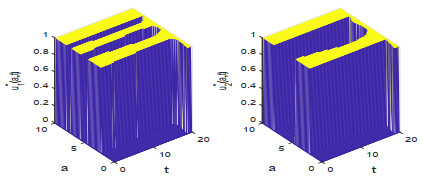
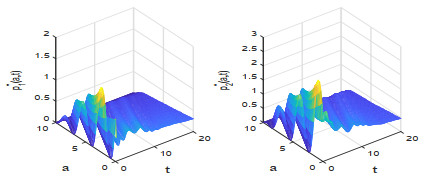
该文研究一类带有年龄等级结构的种群竞争模型的最优收获强度控制问题.证明了最优策略的存在性，关于含有分布式和边界控制函数的偏微分积分系统建立了一个新的连续性定理，据此并运用法锥和共轭系统技巧对最优策略进行了精确刻画.此外，也展示了一些数值实验结果，考察了价格函数对最优收益的影响.

关键词: 年龄等级, 竞争系统, 最优控制, 法锥, 预紧性

Abstract:

In this paper, we investigate an optimal control problem for a hierarchical system of age-dependent competing populations, with the removal intensity as the control variable. After the existence of optimal strategies has been established, we prove a new continuity result, by which the optimal policies are exactly characterized with a normal cone and an adjoint system. Furthermore, some numerical results are presented to show the effects of the price on optimal profits.

Key words: Hierarchy of age, Competing system, Optimal control, Normal cone, Pre-compactness

中图分类号:

O211.4

何泽荣,周楠. 具有年龄等级结构的种群竞争系统的最优收获控制[J]. 数学物理学报, 2022, 42(1): 228-244.

Zerong He,Nan Zhou. Optimal Harvesting in a Competing System of Hierarchical Age-Structured Populations[J]. Acta mathematica scientia,Series A, 2022, 42(1): 228-244.

图/表 9

图 1

最优控制 $u_1^{*}(a, t)$ 与 $u_2^{*}(a, t)$ ( $s=0)$ "

图 1

图 2

最优密度 $p_1^{*}(a, t)$ 与 $p_2^{*}(a, t)$ ( $s=0)$ "

图 2

图 3

最优控制 $u_1^{*}(a, t)$ 与 $u_2^{*}(a, t)$ ( $s=1)$ "

图 3

图 4

最优密度 $p_1^{*}(a, t)$ 与 $p_2^{*}(a, t)$ ( $s=1)$ "

图 4

图 5

最优控制 $u_1^{*}(a, t)$ 与 $u_2^{*}(a, t)$ ( $s=2)$ "

图 5

图 6

最优密度 $p_1^{*}(a, t)$ and $p_2^{*}(a, t)$ ( $s=2)$ "

图 6

图 7

最优控制 $u_1^{*}(a, t)$ 与 $u_2^{*}(a, t)$ ( $s=3)$ "

图 7

图 8

最优密度 $p_1^{*}(a, t)$ 与 $p_2^{*}(a, t)$ ( $s=3)$ "

图 8

表 1

参考文献 33

1	Getz W M , Haight R G . Population Harvesting: Demographic Models of Fish, Forest, and Animal Resources. Princeton: Princeton University Press, 1989
2	Aniţa S . Analysis and Control of Age-Dependent Population Dynamics. Dordrecht: Kluwer Academic Publishers, 2000
3	Lenhart S , Workman J T . Optimal Control Applied to Biological Models. New York: Taylor & Francis Group, 2007
4	Leung A W . Nonlinear System of Partial Differential Equations: Applications to Life and Physical Sciences. Beijing: World Scientific Publishing, 2009
5	Boucekkine R , Hritoenko N , Yatsenko Y . Optimal Control of Age-Structured Populations in Economy, Demography, and the Environment. New York: Routledge, 2011
6	Rorres C , Fair W . Optimal harvesting policy for an age-specific population. Mathematical Biosciences, 1975, 24: 31- 47 doi: 10.1016/0025-5564(75)90065-6
7	Brokate M . Pontryagin's principle for control problems in age-dependent population dynamics. J Math Biology, 1985, 23: 75- 101 doi: 10.1007/BF00276559
8	Medhin N G . Optimal harvesting in age-structured populations. J Optim Theor Appl, 1992, 74 (3): 413- 423 doi: 10.1007/BF00940318
9	Cañada A , Gámez J L , Montero J A . Study of an optimal control problem for diffusive nonlinear elliptic equations of Logistic type. SIAM J Control Optim, 1998, 36 (4): 1171- 1189 doi: 10.1137/S0363012995293323
10	Yamauchi A , Matsummiya Y , Iwasa Y . Optimal age-dependent sustainable harvesting of natural resouece populations: Sustainability value. Res Popul Ecol, 1997, 39 (2): 139- 148 doi: 10.1007/BF02765259
11	Gurtin M E , Murphy L F . On the optimal harvesting of persistent age-structured populations. J Math Biology, 1981, 13: 131- 148 doi: 10.1007/BF00275209
12	Murphy L F , Smith S J . Optimal harvesting of an age-structured population. J Math Biology, 1990, 29: 77- 90
13	Busoni G , Matucci S . A problem of optimal harvesting policy in two-stage age-dependent populations. Mathematical Biosciences, 1997, 43: 1- 33
14	Barbu V , Iannelli M . Optimal control of population dynamics. J Optim Theor Appl, 1999, 102: 1- 14 doi: 10.1023/A:1021865709529
15	Fister K R , Lenhart S . Optimal harvesting in an age-structured predator-prey model. Appl Math Optim, 2006, 54: 1- 15 doi: 10.1007/s00245-005-0847-9
16	Hritoenko N , Yatsenko Y . The structure of optimal time- and age-dependent harvesting in the Lotka-McKendrik population model. Mathematical Biosciences, 2007, 208: 48- 62 doi: 10.1016/j.mbs.2006.09.008
17	Zhao C , Zhao P , Wang M S . Optimal harvesting for nonlinear age-dependent population dynamics. Mathematical and Computer Modelling, 2006, 43: 310- 319 doi: 10.1016/j.mcm.2005.06.008
18	Luo Z . Optimal harvesting problem for an age-dependent n-dimensional food chain diffusion model. Applied Mathematics and Computation, 2007, 186: 1742- 1752 doi: 10.1016/j.amc.2006.08.168
19	Lu D , Gu J , Wang X . Optimal harvesting problems for an age-dependent n-dimensional food chain model with diffusion. Applied Mathematics and Computation, 2007, 184: 659- 668 doi: 10.1016/j.amc.2006.06.065
20	He Z R . Opitmal harvesting of two competing species with age dependence. Nonlinear Analysis: RWA, 2006, 7: 769- 788 doi: 10.1016/j.nonrwa.2005.04.005
21	Braverman E , Braverman L . Optimal harvesting of diffusive models in a nonhomogeneous environment. Nonlinear Analysis, 2009, 71: e2173- e2191 doi: 10.1016/j.na.2009.04.025
22	Dewsbury D A . Dominance rank, copulatory behavior, and differential reproduction. The Quarterly Review of Biology, 1982, 57 (2): 135- 159 doi: 10.1086/412672
23	Cushing J M , Li J . Oscillations caused by cannibalism in a size-structured population model. Canadian Applied Mathematics Quarterly, 1995, 3 (2): 155- 172
24	Cañada A , Saldana J . Asymptotic behaviour of a model of hierarchically structured population dynamics. Journal of Mathematical Biology, 1997, 35 (8): 967- 987 doi: 10.1007/s002850050085
25	Kraev E A . Existence and uniqueness for height structured hierarchical population models. Natural Resource Modeling, 2001, 14 (1): 45- 70 doi: 10.1111/j.1939-7445.2001.tb00050.x
26	Jang R J , Cushing J M . A discrete hierarchical model of intra-specific competition. Journal of Mathematical Analysis and Applications, 2003, 280 (1): 102- 122 doi: 10.1016/S0022-247X(03)00050-7
27	Ackleh A S , Deng K . Monotone approximation for a hierarchical age-structured population model. Dynamics of Continuous, Discrete and Impulsive Systems, 2005, 2 (2): 203- 214
28	Shen J , Shu C W , Zhang M . A high order WENO Scheme for a hierarchical size-structured population model. Journal of Scientific Computing, 2007, 33 (3): 279- 291 doi: 10.1007/s10915-007-9152-x
29	Liu Y , He Z . On the well-posedness of a nonlinear hierarchical size-structured population model. ANZIAM Journal, 2017, 58 (3/4): 482- 490
30	He Z R , Ni D , Wang S P . Optimal harvesting of a hierarchical age-structured population system. International Journal of Biomathematics, 2019, 12 (8): 1950091 doi: 10.1142/S1793524519500918
31	何泽荣, 周楠, 韩梦杰. 年龄等级结构两种群系统模型解的存在唯一性. 数学进展, 2020, 49 (6): 713- 722
	He Z R , Zhou N , Han M J . On the system model of two hierarchical age-structured populations. Advances in Mathematics, 2020, 49 (6): 713- 722
32	Yosida K . Functional Analysis. Beijing: Beijing World Publishing Corporation, 1999
33	Barbu V . Mathematical Methods in Optimization of Differential Systems. Dordrecht: Kluwer Academic Publishers, 1994

相关文章 15

[1]	何泽荣,韩梦杰. 带时滞的尺度等级结构种群系统的最优初始控制[J]. 数学物理学报, 2021, 41(4): 1181-1191.
[2]	刘琼琳,唐应辉. 在 $D$ -策略控制下服务员单重休假且休假不中断的 $M$ / $G$ /1排队系统分析[J]. 数学物理学报, 2021, 41(1): 269-288.
[3]	何泽荣,张智强,王阳. 一类非线性年龄等级结构种群模型的稳定性[J]. 数学物理学报, 2020, 40(6): 1712-1722.
[4]	何泽荣,张智强,裘哲勇. 一类非线性年龄等级结构种群模型的数值解法[J]. 数学物理学报, 2020, 40(2): 515-526.
[5]	罗乐,唐应辉. 具有p-进入规则和Min(N, D, V)-策略的M/G/1排队系统容量问题研究[J]. 数学物理学报, 2019, 39(5): 1228-1246.
[6]	唐矛宁,孟庆欣. 带跳跃平均场倒向随机微分方程的线性二次最优控制[J]. 数学物理学报, 2019, 39(3): 620-637.
[7]	李润鑫,黄辉,尚振宏,曹宇,王红斌,张晶. 多目标约束向量优化问题的类拉格朗日乘数法[J]. 数学物理学报, 2018, 38(6): 1076-1094.
[8]	潘取玉,唐应辉. 在延迟Min (N, D)-策略M/G/1可修排队系统及最优控制策略[J]. 数学物理学报, 2018, 38(5): 1014-1031.
[9]	章春国, 刘宇标, 刘维维. Timoshenko梁的边界最优控制[J]. 数学物理学报, 2018, 38(3): 454-466.
[10]	李周红, 张丰硕, 曹进德, Alsaedi Ahmed, Alsaadi Fuad E. 时标上带有反馈控制的非自治两种群竞争系统的概周期解[J]. 数学物理学报, 2017, 37(4): 730-750.
[11]	高丽君, 唐应辉. 具有Min(N,D)-策略控制的M/G/1可修排队系统及最优控制策略[J]. 数学物理学报, 2017, 37(2): 352-365.
[12]	何泽荣, 杨立志. 具有尺度结构和双加权的种群模型:稳定性与最优收获[J]. 数学物理学报, 2016, 36(3): 584-600.
[13]	何泽荣, 刘荣, 刘丽丽. 模拟周期环境和尺度结构的种群系统的最优收获率[J]. 数学物理学报, 2014, 34(3): 684-690.
[14]	武利猛, 倪明康, 陆海波. 奇摄动最优控制问题中的内部转移层解[J]. 数学物理学报, 2013, 33(2): 206-215.
[15]	刘炎, 何泽荣. 具有Size结构的捕食种群系统的最优收获策略[J]. 数学物理学报, 2012, 32(1): 90-102.

Metrics

Viewed

Full text

126

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	10	0	0	116

	From	local

	Times	126
	Rate	100%

Abstract

140

Just accepted	Online first	Issue

0	0	140

From	Others	local

Times	136	4
Rate	97%	3%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

s	0	1	2	3
J(u^*)	21.0642	24.4689	27.8961	32.1155