数学物理学报 ›› 2021, Vol. 41 ›› Issue (6): 1871-1879.
一个改进的WYL型三项共轭梯度法
- 桂林电子科技大学数学与计算科学学院 & 广西高校数据分析与计算重点实验室 广西桂林 541004
-
收稿日期:2020-11-06出版日期:2021-12-26发布日期:2021-12-02 -
通讯作者:耿远航 E-mail:zhuzb@guet.edu.cn;18434164700@163.com -
作者简介:朱志斌, E-mail:zhuzb@guet.edu.cn -
基金资助:国家自然科学基金(61967004);国家自然科学基金(11901137);广西自动检测技术与仪器重点实验室项目(YQ20113);广西自动检测技术与仪器重点实验室项目(YQ20114);广西密码学与信息安全重点实验室研究课题(GCIS201927);广西密码学与信息安全重点实验室研究课题(GCIS201621);桂林电子科技大学研究生教育创新计划资助项目(2021YCXS118)
A Modified Three-Term WYL Conjugate Gradient Method
- School of Mathematics and Computing Science, Guilin University of Electronic Technology&Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guangxi Guilin 541004
-
Received:2020-11-06Online:2021-12-26Published:2021-12-02 -
Contact:Yuanhang Geng E-mail:zhuzb@guet.edu.cn;18434164700@163.com -
Supported by:the NSFC(61967004);the NSFC(11901137);the Guangxi Key Laboratory of Automatic Detecting Technology and Instruments(YQ20113);the Guangxi Key Laboratory of Automatic Detecting Technology and Instruments(YQ20114);the Guangxi Key Laboratory of Cryptography and Information Security(GCIS201927);the Guangxi Key Laboratory of Cryptography and Information Security(GCIS201621);the Innovation Project of GUET Graduate Education(2021YCXS118)
摘要:
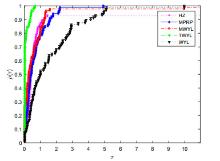
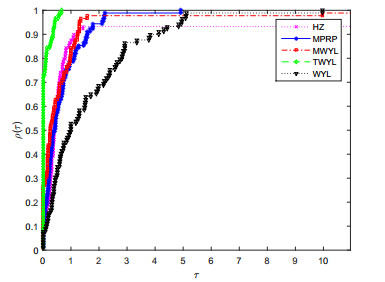
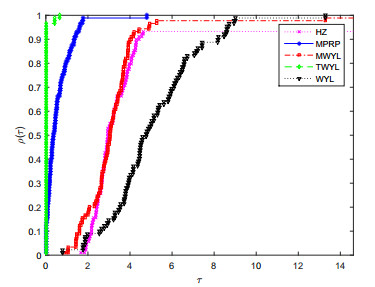
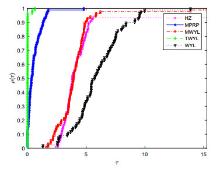
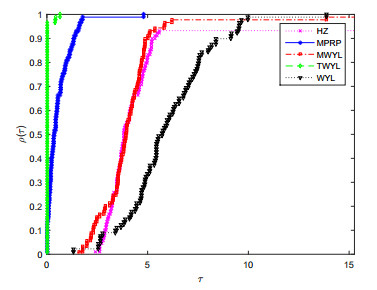
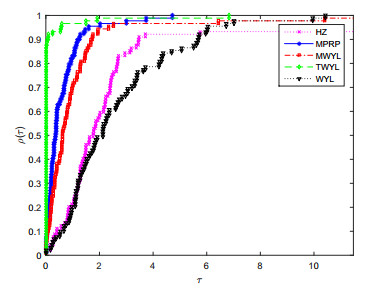
共轭梯度法是求解一类大规模优化问题的重要算法,有计算简单收敛速度快等优点.该文提出了一个修正的WYL型三项共轭梯度法.该方法满足充分下降条件不依赖于任何线搜索方式,并且在修改的Armijo线搜索下具有全局收敛性质.实验数值结果表明新方法是有效的.
中图分类号:
- O221.2
引用本文
朱志斌,耿远航. 一个改进的WYL型三项共轭梯度法[J]. 数学物理学报, 2021, 41(6): 1871-1879.
Zhibin Zhu,Yuanhang Geng. A Modified Three-Term WYL Conjugate Gradient Method[J]. Acta mathematica scientia,Series A, 2021, 41(6): 1871-1879.
使用本文
表 1
测试函数编号及名称"
| Number | Function Name | Number | Function Name | Number | Function Name |
| 1 | Extended Quadratic Penaltyb QP1 | 2 | Extended Penaltyb | 3 | Extended Wood |
| 4 | Diagonal 1 | 5 | Perturbed Quadratic | 6 | Diagonal 3 |
| 7 | Generalized Tridiagonal 1 | 8 | Diagonal 4 | 9 | Diagonal 5 |
| 10 | Extended Himmelblau | 11 | Extended PSC1 | 12 | Extended BD1 (Block Diagonal) |
| 13 | Quadratic QF1 | 14 | Quadratic QF2 | 15 | Extended quadratic exponential EP1 |
| 16 | Extended Tridiagonal 2 | 17 | QUARTC (CUTE) | 18 | Partial Perturbed Quadratic |
| 19 | Almost Perturbed Quadratic | 20 | Staircase 1 | 21 | Diagonal 7 |
| 22 | Diagonal 8 | 23 | Diagonal 9 | 24 | Generalized Quartic |
| 25 | Full Hessian FH3 | 26 | SINCOS | 27 | COSINE (CUTE) |
| 28 | Raydan 1 | 29 | Hager |
表 1
表 2
数值结果"
| N | D | MPRP | WYL | MWYL | HZ | TWYL |
| 1 | 10 | 23/24/24/0.0040 | 99/1059/3218/0.0191 | 13/106/198/0.0053 | 20/110/197/0.0099 | 16/17/17/0.0019 |
| 600 | 21/22/22/0.0120 | 73/1151/2228/0.0342 | 18/100/181/0.0073 | 15/98/178/0.0172 | 11/12/12/0.0071 | |
| 1000 | 15/16/16/0.0047 | 61/933/1804/0.0348 | 18/100/181/0.0049 | 13/86/156/0.0154 | 12/13/13/0.0042 | |
| 2 | 5 | 28/29/29/0.0016 | 29/267/504/0.0029 | 34/140/245/0.0018 | 25/129/230/0.0092 | 19/20/20/0.0012 |
| 20 | 30/31/31/0.0024 | 91/1606/3120/0.0158 | 24/185/345/0.0023 | 24/149/271/0.0102 | 20/21/21/0.0016 | |
| 100 | 46/47/47/0.0061 | 26/254/481/0.0059 | 25/210/394/0.0052 | 21/166/308/0.0095 | 21/22/22/0.0037 | |
| 3 | 100 | 264/265/265/0.0051 | 5768/83377/16098/0.1955 | 270/2520/4769/0.0075 | 322/3115/5905/0.0416 | 169/170/170/0.0040 |
| 500 | 220/221/221/0.0140 | 2154/28471/54787/0.2580 | 426/3895/7363/0.0377 | 525/5062/9596/0.0865 | 213/214/214/0.0141 | |
| 1000 | 264/265/265/0.0298 | 7223/96621/186018/1.5034 | 381/3500/6618/0.0566 | 440/4268/8093/0.0871 | 251/252/252/0.0288 | |
| 4 | 10 | 30/31/31/8.4960e-4 | 37/320/602/0.0013 | 26/144/261/8.5290e-4 | 32/145/255/0.0074 | 22/23/23/6.8260e-4 |
| 100 | 47/48/48/0.0033 | 210/2749/5287/0.0257 | 46/342/637/0.0045 | 50/341/629/0.0145 | 40/41/41/0.0031 | |
| 1000 | 65/66/66/0.0505 | 84/968/1851/0.0765 | 70/601/1251/0.0521 | 93/898/1700/0.0721 | 64/65/65/0.0412 | |
| 5 | 10 | 39/40/40/0.0012 | 87/1845/3602/0.0035 | 37/174/310/7.8290e-4 | 44/233/419/0.0093 | 31/32/32/7.1240e-4 |
| 100 | 128/129/129/0.0026 | 134/1393/2651/0.0046 | 115/851/1586/0.0031 | 131/999/1864/0.0224 | 102/103/103/0.0020 | |
| 1000 | 368/369/369/0.0483 | 480/7022/13563/0.1182 | 402/4059/7715/0.0697 | 545/5637/10726/0.1131 | 337/338/338/0.0465 | |
| 6 | 10 | 33/34/34/0.0014 | 28/205/381/0.0017 | 39/159/278/0.0016 | 28/130/229/0.0063 | 20/21/21/0.0012 |
| 100 | 65/66/66/0.0058 | 69/603/1136/0.0095 | 41/272/502/0.0051 | 68/470/869/0.0206 | 45/46/46/0.0044 | |
| 1000 | 80/81/81/0.0667 | 86/1026/1965/0.1169 | 66/615/1136/0.0704 | 78/756/1431/0.0744 | 71/72/72/0.0616 | |
| 7 | 10 | 53/54/54/0.0032 | 32/303/573/0.0039 | 34/195/355/0.0033 | 31/190/346/0.0073 | 30/31/31/0.0020 |
| 100 | 40/41/41/0.0062 | 400/7132/13863/0.4381 | 31/184/336/0.0069 | 27/164/298/0.0078 | 23/24/24/0.0034 | |
| 1000 | 27/28/28/0.0104 | 30/329/627/0.0292 | 42/241/439/0.0250 | 23/140/254/0.0188 | 19/20/20/0.0078 | |
| 10000 | 23/24/24/0.0718 | 275/5356/10436/4.7556 | 26/150/273/0.1357 | 18/111/201/0.0889 | 14/15/15/0.0452 | |
| 20000 | 23/24/24/0.1684 | 28/310/591/0.5345 | 26/148/269/0.2359 | 16/97/175/0.1371 | 12/13/13/0.0840 | |
| 8 | 10 | 38/39/39/8.1400e-4 | 1171/15199/29226/0.0249 | 74/470/865/0.0013 | 50/359/665/0.0082 | 51/52/52/7.4680e-4 |
| 500 | 42/43/43/0.0021 | 1315/16667/32018/0.0818 | 63/398/732/0.0024 | 54/389/721/0.0062 | 57/58/58/0.0018 | |
| 1000 | 39/40/40/0.0033 | 1341/16869/32396/0.2188 | 70/442/813/0.0064 | 82/584/1083/0.0117 | 62/63/63/0.0048 | |
| 9 | 10 | 3/4/4/0.0011 | 3/7/10/0.0011 | 5/11/16/9.2270e-4 | 7/22/34/0.0016 | 3/4/4/8.9320e-4 |
| 100 | 3/4/4/0.0013 | 3/7/10/0.0010 | 5/11/16/0.0013 | 6/19/29/0.0021 | 3/4/4/0.0010 | |
| 10 | 10 | 48/49/49/0.0017 | 42/665/1287/0.0029 | 54/363/671/0.0020 | 22/165/305/0.0077 | 23/24/24/0.0012 |
| 100 | 52/53/53/0.0020 | 46/728/1409/0.0037 | 57/383/708/0.0026 | 31/230/426/0.0045 | 23/24/24/0.0013 | |
| 1000 | 56/57/57/0.0054 | 48/758/1467/0.0134 | 58/390/721/0.0074 | 27/199/368/0.0054 | 25/26/26/0.0030 | |
| 10000 | 56/57/57/0.0579 | 52/815/1577/0.1831 | 58/390/721/0.1078 | 31/232/430/0.0928 | 29/30/30/0.0517 | |
| 11 | 10 | 16/17/17/0.0014 | 15/58/100/0.0013 | 30/139/247/0.0018 | 18/79/137/0.0034 | 16/17/17/0.0011 |
| 100 | 15/16/16/0.0016 | 15/58/100/0.0014 | 29/134/238/0.0022 | 16/72/125/0.0039 | 15/16/16/0.0014 | |
| 1000 | 15/16/16/0.0039 | 13/51/88/0.0041 | 28/130/231/0.0085 | 16/72/125/0.0052 | 14/15/15/0.0035 | |
| 12 | 10 | 37/38/38/9.3410e-4 | 61/1124/2186/0.0035 | 27/119/210/0.0018 | 28/145/259/0.0046 | 27/28/28/8.0080e-4 |
| 100 | 39/40/40/0.0013 | 65/1175/2284/0.0051 | 27/119/210/0.0012 | 30/156/279/0.0052 | 28/29/29/9.8960e-4 | |
| 1000 | 39/40/40/0.0038 | 69/1223/2376/0.0261 | 28/124/219/0.0034 | 32/166/297/0.0093 | 30/31/31/0.0033 | |
| 13 | 1000 | 376/377/377/0.0308 | 468/5435/10401/0.0547 | 454/4196/7937/0.0429 | 462/4369/8273/0.1338 | 307/308/308/0.0249 |
| 10000 | 1316/1317/1317/3.1568 | 1620/24780/47939/5.6254 | 2791/33598/64404/8.2298 | 1663/20450/39234/7.6030 | 1135/1136/1136/1.6381 | |
| 20000 | 2089/2090/2090/5.7360 | 3224/56220/109215/16.2122 | 4791/61853/118914/18.7639 | 2321/30644/58964/22.2503 | 1613/1614/1614/4.8625 | |
| 14 | 10 | 54/55/55/0.0011 | 121/1623/3124/0.0038 | 38/219/399/0.0013 | 42/257/469/0.0075 | 32/33/33/8.5090e-4 |
| 600 | 321/322/322/0.0206 | 5682/137079/268475/1.1904 | 327/3383/6438/0.0317 | 392/4137/7879/0.0521 | 265/266/266/0.0185 | |
| 1000 | 396/397/397/0.0399 | 501/7736/14970/0.0992 | 469/5196/9922/0.0701 | 518/5796/11071/0.0852 | 348/349/349/0.0378 | |
| 15 | 10 | 60/61/61/0.0019 | 81/1739/3396/0.0056 | 13/115/216/9.7820e-4 | 23/231/436/0.0053 | 17/18/18/8.4180e-4 |
| 100 | 55/56/56/0.0030 | 73/1587/3100/0.0104 | 12/106/199/0.0019 | 21/211/398/0.0052 | 16/17/17/0.0017 | |
| 1000 | 49/50/50/0.0122 | 65/1426/2786/0.0520 | 11/97/182/0.0040 | 17/171/322/0.0070 | 16/17/17/0.0043 | |
| 16 | 1000 | 42/43/43/0.0042 | 33/167/300/0.0062 | 26/86/145/0.0037 | 36/142/245/0.0076 | 26/27/27/0.0034 |
| 10000 | 36/37/37/0.0337 | 15/127/238/0.0404 | 12/43/73/0.0176 | 14/61/105/0.0233 | 15/16/16/0.0210 | |
| 20000 | 32/33/33/0.0580 | 12/76/139/0.0512 | 11/40/68/0.0270 | 10/47/81/0.0316 | 10/11/11/0.0240 | |
| 100000 | 24/25/25/0.1614 | 9/58/106/0.1309 | 9/33/56/0.0811 | 7/36/62/0.0756 | 9/10/10/0.0670 | |
| 17 | 1000 | 1/2/2/0.0149 | 1000/20044/30088/9.3673 | 1000/20001/30002/9.2210 | -/-/-/- | 1/2/2/0.0068 |
| 18 | 10 | 35/36/36/0.0033 | 93/2021/3948/0.0291 | 27/136/244/0.0029 | 26/139/249/0.0066 | 24/25/25/0.0027 |
| 100 | 75/76/76/0.0359 | 80/802/1523/0.0908 | 72/540/1007/0.0594 | 86/673/1257/0.1408 | 72/73/73/0.0319 | |
| 1000 | 334/335/335/51.9645 | 348/5448/10547/98.1685 | 389/4631/8872/78.6427 | 491/5943/11392/90.9052 | 305/306/306/32.5759 | |
| 19 | 10 | 36/37/37/8.8550e-4 | 89/1945/3800/0.0081 | 33/157/280/9.2980e-4 | 43/226/406/0.0050 | 31/32/32/7.7060e-4 |
| 100 | 118/119/119/0.0059 | 142/1620/3097/0.0110 | 116/855/1593/0.0068 | 128/965/1799/0.0209 | 104/105/105/0.0051 | |
| 1000 | 365/366/366/0.0464 | 512/7484/14455/0.1206 | 400/4038/7675/0.0666 | 469/4841/9210/0.0901 | 325/326/326/0.0434 | |
| 10000 | 1140/1141/1141/2.2828 | 2024/36184/70343/7.2277 | 2630/33971/65311/6.6585 | 1606/21180/40751/7.7436 | 1115/1116/1116/2.3376 | |
| 20 | 10 | 111/112/112/0.0038 | 645/6679/12712/0.0377 | 88/550/1011/0.0041 | 120/795/1467/0.0197 | 104/105/105/0.0036 |
| 50 | 581/582/582/0.0448 | 7249/75221/143192/0.8142 | 720/7177/13633/0.0812 | 649/6657/12662/0.1175 | 526/527/527/0.0433 | |
| 100 | 1389/1390/1390/1.1858 | 1461/23309/45156/1.9609 | 1580/18355/35129/1.7259 | 1436/17161/32883/0.4488 | 1096/1097/1097/0.6747 | |
| 21 | 1000 | 23/24/24/0.0713 | 26/317/607/0.0249 | 8/24/39/0.0027 | 10/41/69/0.0167 | 12/13/13/0.0040 |
| 10000 | 30/31/31/0.0016 | 20/227/433/1.5810 | 7/21/34/0.1396 | 9/37/62/0.0854 | 9/10/10/0.1825 | |
| 20000 | 24/25/25/0.5173 | 20/226/431/3.2724 | 7/21/34/0.2893 | 9/37/62/0.1277 | 9/10/10/0.3605 | |
| 22 | 100 | 30/31/31/0.0016 | 18/183/347/0.0025 | 11/32/54/0.0011 | 12/49/83/0.0042 | 11/12/12/0.0011 |
| 10000 | 24/25/25/0.0418 | 12/106/199/0.0825 | 9/27/44/0.0197 | 10/41/69/0.0476 | 8/9/9/0.0189 | |
| 20000 | 23/24/24/0.0713 | 10/83/155/0.1243 | 9/27/44/0.0377 | 10/41/69/0.0590 | 8/9/9/0.0342 | |
| 23 | 10000 | 103/104/104/0.8917 | 101/1647/3192/1.1939 | 92/1200/2307/0.9328 | 94/1242/2387/0.8362 | 91/92/92/0.7481 |
| 20000 | 59/60/60/0.8852 | 73/1302/2530/1.8032 | 68/895/1721/1.2813 | -/-/-/- | 58/59/59/0.8296 | |
| 100000 | 64/65/65/5.0643 | 108/2333/4557/15.1715 | 71/1174/2276/7.5531 | -/-/-/- | 54/55/55/4.3003 | |
| 24 | 10000 | 20/21/21/0.0138 | 137/3270/6402/0.5786 | 20/63/105/0.0138 | 30/122/211/0.0609 | 18/19/19/0.0110 |
| 15000 | 23/24/24/0.0203 | 137/3261/6384/1.0262 | 19/60/100/0.0261 | 31/124/214/0.0910 | 21/22/22/0.0210 | |
| 20000 | 22/23/23/0.0324 | 137/3253/6368/1.2361 | 19/58/96/0.0228 | 31/124/214/0.1063 | 18/19/19/0.0199 | |
| 25 | 50 | 36/37/37/0.0019 | 243/5487/10730/0.0282 | 17/113/208/0.0081 | 46/370/691/0.0127 | 18/19/19/0.0014 |
| 100 | 37/38/38/0.0200 | 103/2346/4588/0.0313 | 23/176/328/0.0025 | 30/270/507/0.0125 | 25/26/26/0.0095 | |
| 1000 | 449/450/450/0.2043 | 72/1683/3293/0.0947 | -/-/-/- | 29/345/658/0.0351 | 15/16/16/0.0153 | |
| 26 | 10000 | 14/15/15/0.0301 | 12/47/81/0.0342 | 28/130/231/0.1007 | 15/67/116/0.0788 | 12/13/13/0.0321 |
| 20000 | 14/15/15/0.0546 | 12/47/81/0.0696 | 28/129/229/0.1529 | 15/67/116/0.1037 | 11/12/12/0.0477 | |
| 100000 | 13/14/14/0.2266 | 11/44/76/0.2716 | 27/126/224/0.6975 | 11/50/86/0.2511 | 11/12/12/0.2078 | |
| 27 | 100 | 46/47/47/0.0035 | 55/656/1256/0.0103 | 25/253/480/0.0049 | -/-/-/- | 19/20/20/0.0020 |
| 1000 | 23/24/24/0.0197 | 73/1332/2590/0.1416 | 16/162/307/0.0195 | -/-/-/- | 14/15/15/0.0071 | |
| 10000 | 16/17/17/0.0686 | 106/1118/2129/1.2885 | 15/114/212/0.1380 | -/-/-/- | 15/16/16/0.0618 | |
| 28 | 10000 | 64/65/65/0.2786 | 73/808/1542/0.4350 | 48/452/855/0.2320 | 73/712/1348/0.4219 | 58/59/59/0.2042 |
| 50000 | 55/56/56/1.1709 | 159/2313/4466/4.1139 | 46/527/1007/1.3277 | 86/1025/1961/3.5063 | 40/41/41/0.8828 | |
| 100000 | 45/46/46/2.0890 | 45/735/1460/3.7004 | 49/605/1160/2.8631 | 39/488/934/3.8924 | 33/34/34/1.6141 | |
| 29 | 1000 | 30/31/31/0.0209 | 25/175/324/0.0167 | 28/147/265/0.0141 | 26/142/255/0.0237 | 22/23/23/0.0099 |
| 10000 | 21/22/22/0.1070 | 52/774/1495/0.7530 | 22/152/281/0.1586 | 21/150/276/0.1327 | 21/22/22/0.1054 | |
| 20000 | 20/21/21/0.2274 | 22/308/593/0.5727 | 19/182/344/0.3380 | 21/153/282/0.2527 | 19/20/20/0.2101 |
表 2
| 1 |
Hestenes M R , Stiefel E . Methods of conjugate gradients for solving linear systems. J Res Natl Bur Stand, 1952, 49 (6): 409- 436
doi: 10.6028/jres.049.044 |
| 2 |
Fletcher R , Reeves C M . Function minimization by conjugate gradients. Comput J, 1964, 7 (2): 149- 154
doi: 10.1093/comjnl/7.2.149 |
| 3 | Polak E , Ribiere G . Note sur la convergence de méthodes de directions conjuguées. ESAIM-Math Model Num, 1969, 16 (3): 35- 43 |
| 4 |
Polyak B T . The conjugate gradient method in extremal problems. USSR Comput Math Math Phys, 1969, 9 (4): 94- 112
doi: 10.1016/0041-5553(69)90035-4 |
| 5 |
Dai Y H , Yuan Y . A nonlinear conjugate gradient method with a strong global convergence property. SIAM J Optimiz, 1999, 10 (1): 177- 182
doi: 10.1137/S1052623497318992 |
| 6 |
Powell M J D . Convergence properties of algorithms for nonlinear optimization. SIAM Rev, 1986, 28 (4): 487- 500
doi: 10.1137/1028154 |
| 7 |
Glibert J C , Nocedal J . Global convergence properties of conjugate gradient method for optimization. SIAM J Optimiz, 1992, 2 (1): 21- 42
doi: 10.1137/0802003 |
| 8 | Wei Z X , Yao S W , Liu L Y . The convergence properties of some new conjugate gradient methods. Appl Math Comput, 2006, 183 (2): 1341- 1350 |
| 9 | Huang H , Wei Z X , Yao S W . The proof of the sufficient descent condition of the Wei-Yao-Liu conjugate gradient method under the strong Wolfe-Powell line search. Appl Math Comput, 2007, 189 (2): 1241- 1245 |
| 10 | Jiang X Z , Jian J B . Two modified nonlinear conjugate gradient methods with disturbance factors for unconstrained optimization. Nonlinear Dyn, 2014, 77 (1/2): 387- 397 |
| 11 | Zhang L , Jian S Y . Further studies on the Wei-Yao-Liu nonlinear conjugate gradient method. Appl Math Comput, 2013, 219 (14): 7616- 7621 |
| 12 | Lu S , Wei Z X , Mo L L . Some global convergence properties of the Wei-Yao-Liu conjugate gradient method with inexact line search. Appl Math Comput, 2011, 217 (17): 7132- 7137 |
| 13 | Yao S W , Wei Z X , Huang H . A note about WYLs conjugate gradient method and its application. Appl Math Comput, 2007, 191 (2): 381- 388 |
| 14 | Zhang P , Du X W . A hybrid PRP-WYL conjugate gradient method with the strong wolfe line search. Journal of Chongqing Normal University, 2020, 37 (1): 41- 51 |
| 15 |
Zhang L , Zhou W J , Li D H . A descent modified Polak-Ribiére-Polyak conjugate gradient method and its global convergence. IMA J Numer Anal, 2006, 26 (4): 629- 640
doi: 10.1093/imanum/drl016 |
| 16 | 李向荣. 一个三项LS共轭梯度方法. 广西科学, 2013, 20 (4): 348- 351 |
| Li X R . A three-term LS conjugate gradient method. Guangxi Sciences, 2013, 20 (4): 348- 351 | |
| 17 |
Liu J K , Zhao Y X , Wu X L . Some three-term conjugate gradient methods with the new direction structure. Appl Numer Math, 2020, 150, 433- 443
doi: 10.1016/j.apnum.2019.10.011 |
| 18 |
Amini K , Faramarzi P , Pirfalah N . A modified Hestenes-Stiefel conjugate gradient method with an optimal property. Optim Method Softw, 2019, 34 (4): 770- 782
doi: 10.1080/10556788.2018.1457150 |
| 19 |
Wu Y L . A modified three-term PRP conjugate gradient algorithm for optimization models. J Inequal Appl, 2017, 2017 (1): 1- 14
doi: 10.1186/s13660-016-1272-0 |
| 20 |
Babaie-Kafaki S , Ghanbari R . Two modified three-term conjugate gradient methods with sufficient descent property. Optim Lett, 2014, 8 (8): 2285- 2297
doi: 10.1007/s11590-014-0736-8 |
| 21 | 董晓亮, 李卫军. 一类新的WYL型共轭梯度法及其全局收敛性. 河南师范大学学报(自然科学版), 2018, 46 (4): 107- 112 |
| Dong X L , Li W J . Global convergence of a new Wei-Yao-Liu type conjugate gradient method. Journal of Henan Normal University(Natural Science Edition), 2018, 46 (4): 107- 112 | |
| 22 | Neculai A . An unconstrained optimization test functions collection. Adv Model Optim, 2008, 10 (1): 147- 161 |
| 23 |
Hager W W , Zhang H C . A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J Optimiz, 2005, 16 (1): 170- 192
doi: 10.1137/030601880 |
| 24 | Dlan E D , Moré J J . Benchmarking optimization software with performance profiles. Math Program, 2001, 91 (2): 201- 213 |
| [1] | 马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847. |
| [2] | 迟晓妮,曾荣,刘三阳,朱志斌. 对称锥权互补问题的正则化非单调非精确光滑牛顿法[J]. 数学物理学报, 2021, 41(2): 507-522. |
| [3] | 马国栋. 一般约束极大极小优化问题一个强收敛的广义梯度投影算法[J]. 数学物理学报, 2020, 40(3): 641-649. |
| [4] | 李向利,师娟娟,董晓亮. 一类修正的非单调谱共轭梯度法及其在非负矩阵分解中的应用[J]. 数学物理学报, 2018, 38(5): 954-962. |
| [5] | 胡朝明, 万中, 王旭. 一种新的非单调谱共轭梯度算法[J]. 数学物理学报, 2013, 33(1): 78-88. |
| [6] | 汤京永, 贺国平. 二阶锥规划的一步光滑牛顿法[J]. 数学物理学报, 2012, 32(4): 768-778. |
| [7] | 房亮, 贺国平, 王永丽. 带有P0函数的非线性互补问题的一个新的非内点连续算法[J]. 数学物理学报, 2011, 31(1): 229-238. |
| [8] | 张丽; 周伟军. Armijo线性搜索下Hager-Zhang共轭梯度法的全局收敛性[J]. 数学物理学报, 2008, 28(5): 840-845. |
| [9] | 童小娇;何伟. 解非线性约束方程的拉格朗日全局投影方法[J]. 数学物理学报, 2008, 28(1): 96-108. |
| [10] | 周长银; 贺国平; 王永丽. 基于有效约束识别技术的一个SSLE算法及其收敛性分析[J]. 数学物理学报, 2007, 27(3): 535-540. |
| [11] | 时贞军. 精确搜索下的非线性共轭梯度法[J]. 数学物理学报, 2004, 4(6): 675-682. |
| [12] | 高自友, 任华玲, 贺国平. 无严格互补松驰条件的序列线性方程组新算法[J]. 数学物理学报, 2004, 24(3): 275-284. |
| [13] | 施保昌, 陈珽, 祝世京. 多目标决策的中心方法之统一探讨[J]. 数学物理学报, 1997, 17(S1): 15-22. |
|
||