| 1 |
Coifman R R , Weiss G . Analyse Harmonique Non-commutative sur Certain Espaces Homogènes. Berlin: Springer-Verlag, 1971
|
| 2 |
Coifman R R , Weiss G . Extensions of Hardy spaces and their use in analysis. Bull Amer Math Soc, 1977, 83 (4): 569- 645
|
| 3 |
Hu G , Lin H , Yang D . Marcinkiewicz integrals with non-doubling measures. Integral Equations Operator Theory, 2007, 58 (2): 205- 238
|
| 4 |
陈冬香, 吴丽丽. 具有非倍测度的Marcinkiewicz积分交换子在Morrey空间的有界性. 数学物理学报, 2011, 31A (4): 1105- 1114
|
|
Chen D X , Wu L L . The boundedness of the commutators for Marcinkiewicz integral with nondoubling measures on Morrey spaces. Acta Math Sci, 2011, 31A (4): 1105- 1114
|
| 5 |
Wang S , Jiang Y , Li B . Weighted estimates for Marcinkiewicz integrals with non-doubling measures. J Math Res Appl, 2012, 32 (2): 223- 234
|
| 6 |
Zhang J , Jiang Y . The boundeness of Marcinkiewicz integral commutators with non-doubling measures in Herz spaces. J Math, 2010, 30 (6): 966- 972
|
| 7 |
Tolsa X .    , ,   and Calderón-Zygmund operators for non-doubling measures. Math Ann, 2001, 319 (1): 89- 149 and Calderón-Zygmund operators for non-doubling measures. Math Ann, 2001, 319 (1): 89- 149
|
| 8 |
Tolsa X . Littlewood-Paley theory and the     theorem with non-doubling measures. Adv Math, 2001, 164 (1): 57- 116 theorem with non-doubling measures. Adv Math, 2001, 164 (1): 57- 116
|
| 9 |
Hytönen T . A framework for non-homogeneous analysis on metric spaces, and the RBMO space of Tolsa. Publ Mat, 2010, 54 (2): 485- 504
|
| 10 |
Lin H , Yang D . Equivalent boundedness of Marcinkiewicz integrals on non-homogeneous metric measure spaces. Sci China Math, 2014, 57 (1): 123- 144
|
| 11 |
Li H , Lin H . Boundedness of Marcinkiewicz integrals on Hardy spaces   over non-homogeneous metric measure spaces. J Math Inequal, 2018, 12 (2): 347- 364 over non-homogeneous metric measure spaces. J Math Inequal, 2018, 12 (2): 347- 364
|
| 12 |
Fu X , Yang Da , Yang Do . The molecular characterization of the Hardy space   on nonhomogeneous metric measure spaces and its application. J Math Anal Appl, 2014, 410 (2): 1028- 1042 on nonhomogeneous metric measure spaces and its application. J Math Anal Appl, 2014, 410 (2): 1028- 1042
|
| 13 |
Lu G , Tao S . Generalized Morrey spaces over non-homogeneous metric measure spaces. J Aust Math Soc, 2017, 103 (2): 268- 278
|
| 14 |
韩瑶瑶, 赵凯. 非齐度量测度空间上的Herz型Hardy空间. 中国科学:数学, 2018, 48 (10): 1315- 1338
|
|
Han Y Y , Zhao K . Herz type Hardy spaces on non-homogeneous metric measure space. Sci Sin Math, 2018, 48 (10): 1315- 1338
|
| 15 |
Lu G , Tao S . Fractional type Marcinkiewicz commutators over non-homogeneous metric measure spaces. Anal Math, 2019, 45 (1): 87- 110
|
| 16 |
陶双平, 逯光辉. Morrey空间上Marcinkiewicz积分与    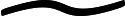    交换子. 数学学报(中文版), 2019, 62 (2): 269- 278 交换子. 数学学报(中文版), 2019, 62 (2): 269- 278
|
|
Tao S P , Lu G H . Commutators of Marcinkiewicz integrals with     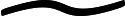    on Morrey space. Acta Math Sin (Chinese Ser), 2019, 62 (2): 269- 278 on Morrey space. Acta Math Sin (Chinese Ser), 2019, 62 (2): 269- 278
|
| 17 |
Htyönen T , Yang Da , Yang Do . The Hardy space   on non-homogeneous metric measure spaces. Math Proc Camb Philos Soc, 2012, 153 (1): 9- 31 on non-homogeneous metric measure spaces. Math Proc Camb Philos Soc, 2012, 153 (1): 9- 31
|
| 18 |
Ri C , Zhang Z . Boundedness of  -type Calderón-Zygmund operaors on non-homoge-neous metric measure spaces. Front Math in China, 2016, 11 (1): 141- 153 -type Calderón-Zygmund operaors on non-homoge-neous metric measure spaces. Front Math in China, 2016, 11 (1): 141- 153
|
| 19 |
Fu X , Yang Da , Yuan W . Generalized fractional integral and their commutators over non-homogeneous metric measure spaces. Taiwanese J Math, 2014, 18 (2): 509- 557
|
| 20 |
Fu X , Lin H , Yang Da , Yang Do . Hardy space   over non-homogeneous metric measure spaces and their applications. Sci China Math, 2015, 58 (2): 309- 388 over non-homogeneous metric measure spaces and their applications. Sci China Math, 2015, 58 (2): 309- 388
|
| 21 |
Lin H , Wu S , Yang D . Boundedness of certain commutators over non-homogeneous metric measure spaces. Anal Math Phys, 2017, 7 (2): 187- 218
|
| 22 |
Cao Y, Zhou J. The boundedness of Marcinkiewicz integrals commutators on non-homogeneous metric measure spaces. J Inequal Appl, 2015, Article number: 259
|
| 23 |
Bui T , Duong X . Hardy spaces, regularized BMO and the boundedness of Calderón-Zymgund operators on homogeneous spaces. J Geom Anal, 2013, 23 (2): 895- 932
|