在过去的几十年里, 分数阶导数和积分为描述非局部性和记忆特征的现象提供一个很好的工具, 如模拟真实材料的力学和电学性能、聚合物和岩石的流变特性等^[1,2]. 分数阶导数和分数阶微分方程在生物学、物理学、化学等众多科学领域中也得到非常广泛的应用, 如: 异常扩散现象、分数布朗运动等^[3⇓-5]. 时间分数阶扩散方程的分数阶 $0<\alpha<1$ 时, 表示亚扩散现象, $1<\alpha<2$ 时, 表示超扩散现象. 时间分数阶扩散方程可以用于描述复杂粘弹性材料中的松弛现象^[6]、连续时间随机游动^[7]、非均匀多孔介质的异常运输^[8], 集成 Kalman 滤波器^[9]等.

时间分数阶扩散方程的正问题得到广泛的研究^[10⇓-12]. 对于时空分数阶扩散方程反问题也有一定的研究成果, 文献[13]提出一种迭代方法去确定非线性时空分数阶扩散方程的系数参数, 并给出该迭代算法的数值仿真实例. 文献[14]采用拟边界正则化方法求解非齐次时空分数阶扩散方程的反初值问题, 给出误差估计, 通过一维和二维情况下的数值结果表明该正则化方法是有效且稳定的. 文献[15]提出一种基于极小化问题、最速下降法和最小二乘法的离散数值方法, 用该方法求解时空分数阶扩散方程的未知源项反问题. 文献[16]应用傅里叶截断正则化方法识别时空分数阶扩散方程中的未知源项, 并给出先验和后验误差估计. 文献[17] 通过 Bayesian 方法确定时空分数阶扩散方程的源函数及时间和空间分数阶导数的阶数, 并采用迭代集成 Kalman 法对一维情况进行数值实现. 其他相关文献见^{[18⇓⇓⇓-22]}.

关于时间分数阶扩散波动方程反问题的研究很有限, 对于时间分数阶 (不含空间分数阶导数) 扩散波动方程反问题的研究有很多. 文献[23]对多维分数阶扩散波动方程的逆源问题进行研究, 利用共轭梯度法结合 Morozov 不一致原理对其变分问题进行求解. 文献[24]使用非平稳迭代 Tikhonov 正则化方法结合有限维逼近得到多维时间分数阶扩散波动方程的一个稳定的源项, 再通过数值算例证明该方法的有效性. 文献[25]通过变分正则化方法识别时间分数阶扩散波动方程的未知源项, 再通过数值实验验证该方法的有效性和鲁棒性. 文献[26]利用非平稳迭代 Tikhonov 正则化方法的数值算法同时恢复时间分数阶扩散波动方程中随时间变化的势系数和源项, 给出数值例子说明该数值算法的有效性和鲁棒性. 还有一些有关时间分数阶扩散波动方程识别初值的研究, 文献[27]应用 Tikhonov 正则化方法求解时间分数阶扩散波动方程的初值识别问题. 在文献[28]中, 采用三种 Landweber 迭代正则化方法求解球对称区域上时间分数扩散波动方程识别初值的反问题, 并分别给出精确解与这几种正则解的先验和后验误差估计式, 最后通过数值算例说明三种正则化方法的有效性. 文献[29]研究有界域内时间分数阶扩散波动方程的后向问题, 讨论解的存在性、唯一性和稳定性, 给出精确解与 Tikhonov 正则化解之间的先验和后验误差估计, 并通过数值结果表明 Tikhonov 正则化方法是有效的. 文献[30]采用 Fourier 截断正则化方法恢复特殊有界域上时间分数阶非齐次扩散波动方程初值的稳定性, 并给出先验和后验误差估计式及数值例子说明 Fourier 截断正则化方法是有效的.

对同时具有时间和空间分数阶导数的扩散波动方程反问题的研究很少. 文献[31]利用分数阶 Landweber 迭代正则化方法求解时空分数阶扩散波动方程的未知源项识别问题, 给出该反问题的条件稳定性和收敛速度, 再通过一维和二维数值实验证明该正则化方法的有效性. 文献[32]采用 Landweber 迭代正则化方法求解时空分数阶扩散波动方程的初值识别问题, 给出先验和后验误差估计, 通过一维和二维数值结果验证该方法的有效性和稳定性.

本文考虑以下时空分数阶扩散波动方程, 设 $\Omega\in {R}^{d}~(d \geq 1)$ 是具有光滑边界 $\partial\Omega$ 的有界域. $T>0$ 是固定时间, 有

其中 $v>0$ 和 $0<\gamma<\beta\leq 1$ 是常数, $\varphi(x)$ 和 $\psi(x)$ 是定义在 $L^2(\Omega)$ 上的初始数据, 算子 $\partial_{t}^{\alpha}u(x,t)$ 为 $\alpha~(1<\alpha<2)$ 阶的 Caputo 分数阶导数, 定义如下

其中 $\Gamma(\cdot)$ 表示 Gamma 函数. 算子$(-\Delta)^s$ 是分数阶 Laplace 算子, 定义如下^[33]

其中$C_{d,s}=\frac{4^s\Gamma(d/2+s)}{\pi^{d/2}|\Gamma(-s)|}$.

在问题(1.1)中, 如果初值 $\varphi(x)$ 和 $\psi(x)$ 已知, 那么该问题是一个正问题. 如果初值 $\varphi(x)$ 和 $\psi(x)$ 未知, 利用终值数据 $u(x,T)=g(x)$ 识别未知初值 $\varphi(x)$ 和 $\psi(x)$, 这是反问题. 在实际问题中, 终值数据是通过测量得到, 会带有误差, 假设精确数据 $g(x)$ 与测量数据 $g^{\delta}(x)$ 满足

其中 $\|\cdot\|$ 表示 $L^{2}(\Omega)$ 范数, $\delta>0$ 是测量误差.

本文中, 将上述反问题分为以下两个反问题进行求解

(BP1) 假设 $\psi(x)$ 是已知的, 用测量数据 $g^{\delta}(x)$ 反演初值 $\varphi(x)$.

(BP2) 假设 $\varphi(x)$ 是已知的, 用测量数据 $g^{\delta}(x)$ 反演初值 $\psi(x)$.

本文的结构如下. 第二部分为辅助性结论. 第三部分给出问题 (1.1) 的解, 分析解的不适定性, 并给出稳定性结果. 第四部分, 利用 Tikhonov 正则化方法恢复解的稳定性, 分别给出初值 $\varphi(x)$ 和 $\psi(x)$ 在先验和后验正则化参数选取规则下的误差估计. 第五部分, 利用数值算例说明 Tikhonov 正则化方法的有效性. 第六部分为主要结论.

定义2.1 在区域 $\Omega$ 上, 设 $\{\lambda_{j}\}_{j=1}^{\infty}$ 和 $\{e_{j}\}_{j=1}^{\infty}$ 分别为算子 $(-\Delta)^s$ 的特征值和特征函数, 且满足

其中 $0< \lambda_{1}\leq\lambda_{2}\leq \cdots\leq \lambda_{j}\leq \cdots$, $\lim\limits_{j\rightarrow\infty}\lambda_{j}=+\infty$ 和 $e_{j}(x)\in H^{2}(\Omega)\cap H_{0}^{1}(\Omega)$, $\{e_{j}\}_{j=1}^{\infty}$ 为空间 $L^{2}(\Omega)$ 中的一组标准正交基.

定义2.2 对于任意的 $p>0$, 定义范数

其中 $(\cdot,\cdot)$ 表示空间 $L^{2}(\Omega)$ 上的内积, $D((-\Delta)^s)$ 是 Hilbert空间, 定义如下

定义2.3^[1,34] Mittag-leffler 函数定义如下

其中 $\alpha>0$ 和 $\beta\in R$ 是任意常数.

引理2.1^[34] 设 $a>0$, Mittag-leffler 函数的 Laplace 变换公式为

其中 $E_{{\alpha,{\beta}}}^{(m)}(y):=\frac{d^m}{dy^m}E_{{\alpha},{\beta}}(y)$.

引理2.2^[1] 如果 $0<\alpha<2$ 和 $\beta\in R$ 是任意常数. 假设 $\mu$ 满足 $\frac{\mu\alpha}{2}<\mu<\min\{\pi, \pi\alpha\}$, 那么存在常数 $C=C(\alpha,\beta,\mu)$ 使得

引理2.3^[1] 对任意的 $1<\alpha<2$, $\beta\in R$ 和 $\eta>0$, 有以下式子成立

引理2.4 对任意的 $T>0$和 $1<\alpha<2$, 存在一个有限集 $I_1=\{j_1,j_2,\cdots,j_J\}$ 使得对任意的 $j\in I_1$ 有 $E_{{\alpha},{1}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})=0$, 对 $j\not\in I_1$ 时有 $E_{{\alpha},{1}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})\neq0$. 而且, 存在有限集 $I_2=\{n_1,n_2,\cdots,n_N\}$ 使得对任意的 $j\in I_2$ 有$E_{{\alpha},{2}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})=0$, 对 $j\not\in I_2$ 时有 $E_{{\alpha},{2}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})\neq0$.

证 从引理 2.3 知, 存在 $L_0>0$ 使得

当 $1<\alpha<2$ 时, 当且仅当 $\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha}\leq L_0$ 时有 $E_{{\alpha},{1}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})=0$. 由于 $\lim\limits_{j\rightarrow\infty}\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}=+\infty$, 所以使$\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha}\leq L_0$ 成立的 $j$ 是有限的. $E_{{\alpha},{2}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})$ 的证明同理, 故省略.证毕.

引理2.5 设$\lambda_j$ 满足 $0<\lambda_1\leq\lambda_j$, 存在依赖于 $\alpha$, $T$, $v$ 及 $\lambda_1$ 的正常数 $C_1$ 和 $C_2$ 使得

其中 $C_1:=\min\{C_3,C_4\}$, $C_2:=\frac{(m+v)C}{T^\alpha}$, $m=\left\{ \begin{array}{ll} 1, & \lambda_1\geq 1, \\ \frac{1}{\lambda_1},\: & \lambda_1<1. \end{array} \right.$

证 令$m=\left\{ \begin{array}{ll} 1, & \lambda_1\geq 1, \\ \frac{1}{\lambda_1},\: & \lambda_1<1, \end{array} \right.$故有 $1+v\lambda_{j}^{\gamma}\leq(m+v)\lambda_{j}^{\gamma}$. 利用引理 2.2 可得

从引理 2.3 知, 存在 $L_0>0$ 使得

又因为$\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha}<\frac{T^\alpha}{v}\lambda_{j}^{\beta-\gamma}$, 所以 $\frac{T^\alpha}{v}\lambda_{j}^{\beta-\gamma}>L_0$, 那么存在 $C_3>0$ 使得

因为 $\lim\limits_{j\rightarrow\infty}\lambda_j=+\infty$, 故只有有限个 $\lambda_{j}$ 满足 $\lambda_{j}^{\beta-\gamma}\leq\frac{L_0v}{T^\alpha}$, 令 $\lambda_j$ 为 $\lambda_{1},\lambda_{2},\cdots,\lambda_{J}$. 那么 $I_1\subset\{1,2,\cdots,J\}$. 对 $j\not\in I_1$, $E_{{\alpha},{1}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})\neq0$, 那么存在一个只依赖于 $\lambda_{1},\lambda_{2},\cdots,\lambda_{J},\:T,\:\alpha,\:v$ 的正常数 $C_4$ 使得

令 $C_1=\min\{C_3,C_4\}$, 那么

$E_{{\alpha},{2}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})$的证明同理, 故省略.证毕.

引理2.6 对任意的 $p > 0$, $0<\mu <1 $, $T > 0$, $0<\lambda_{1}\leq s$ 和正常数 $a$, 有以下不等式成立

其中 $C_{11}:=(4-p)^{\frac{4-p}{4}}p^{\frac{p}{4}}a^{-\frac{p}{4}}$, $C_{12}:=\frac{1}{a}\lambda_{1}^{2-\frac{p}{2}}$.

证 当 $0< p <4$ 时,有

令 $G^{'}(s_1)=0$, 那么

故有

当 $p \geq4$ 时,有

结合(2.11)和(2.12)式, 有(2.10)式成立. 证毕.

引理2.7 对任意的 $p > 0$, $0<\mu <1 $, $T > 0$, $0<\lambda_{1}\leq s$ 和正常数 $b$, 有以下不等式成立

其中 $C_{21}:=(2-p)^{\frac{2-p}{4}}(2+p)^{\frac{2+p}{4}}b^{-\frac{2+p}{4}}$, $C_{22}:=\frac{1}{b}\lambda_{1}^{1-\frac{p}{2}}$.

证 该证明与引理 2.6 的证明同理, 故省略.

通过分离变量法和 Laplace 变换得到问题 (1.1) 的解为

其中 $\varphi_{j}=(\varphi(x),e_{j}(x))$ 和$\psi_{j}=(\psi(x),e_{j}(x))$ 是 Fourier 系数.

由 $u(x,T)=g(x)$ 得

定义

那么

定义算子 $K_1:\varphi(\cdot)\longrightarrow g_1(\cdot)$ 和 $K_2:\psi(\cdot)\longrightarrow g_2(\cdot)$, 问题(1.1)可转换为以下算子方程

将算子 $K_1$ 和算子 $K_2$ 的核函数分别表示为

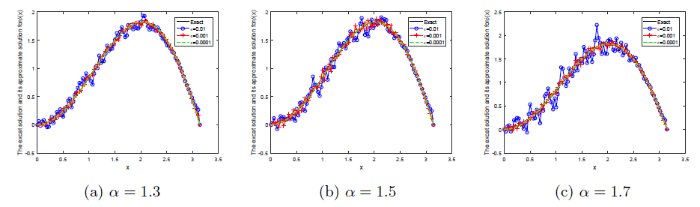
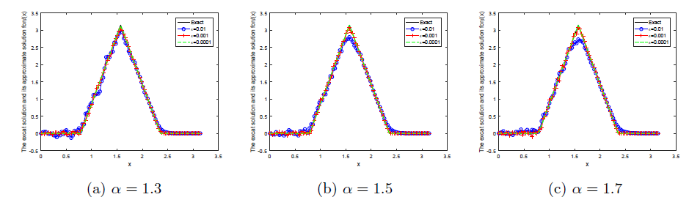
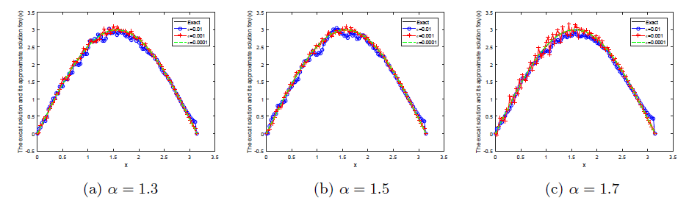
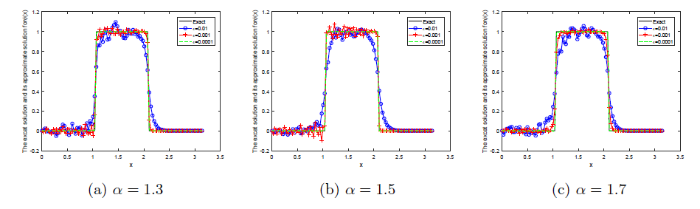
由于 $\kappa_1(x,\xi)=\kappa_1(\xi,x)$ 且 $\kappa_2(x,\xi)=\kappa_2(\xi,x)$,那么算子 $K_1$ 和 $K_2$ 是自共轭算子.根据文献[29]可知 $K_1$ 和 $K_2$ 都是紧算子,因此问题(BP1)和(BP2)是不适定问题.

$K_{1}^{*}$ 是 $K_1$ 的自伴算子, 又 $\{e_j\}_{j=1}^{\infty}$ 是 $L^2(\Omega)$ 内的一组标准正交基, 那么

所以, $K_1$ 的奇异核为 $\sigma_{j}^{(1)}=\Big|E_{{\alpha},{1}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})\Big|$. 定义

由 (3.12) 式可知, $\{Y_{j}^{(1)}\}_{j=1}^{\infty}$ 在 $L^2(\Omega)$ 内是正交的, 故有

所以, $K_1$ 的奇异系统为 $(\sigma_{j}^{(1)}, e_j, Y_{j}^{(1)})$.

同理可得, $K_2$ 的奇异系统为 $(\sigma_{j}^{(2)},e_j,Y_{j}^{(2)})$, 其中 $\sigma_{j}^{(2)}=\Big|TE_{{\alpha},{2}}(-\frac{\lambda_{j}^{\beta}}{1+v\lambda_{j}^{\gamma}}T^{\alpha})\Big|$ 且

注3.1 本文将 $\kappa_1=\emptyset$ 且 $\kappa_2=\emptyset$时, 算子 $K_1$ 和 $K_2$ 的核函数分别为 (3.9) 和 (3.10)式的情况作为特殊情况.

下面, 讨论 $\kappa_1\neq\emptyset$ 和 $\kappa_2\neq\emptyset$ 的一般情况. 此时, 算子 $K_1$ 和 $K_2$ 的核函数分别为

算子 $K_1$ 和 $K_2$ 的核空间表示为

且算子 $K_1$ 和 $K_2$ 的范围为

定理3.1 如果 $\kappa_1=\emptyset$, 那么对任意的 $g_1\in R(K_1)$, 问题 (BP1) 的精确解为

如果 $\kappa_1\neq\emptyset$, 那么对任意的 $g_1\in R(K_1)$, 积分方程 (3.7) 存在无穷多个解, 但是在 $L^2(\Omega)$ 空间内只有一个最佳近似解

证 由积分方程 (3.7) 易得.

定理3.2 如果 $\kappa_2=\emptyset$, 对任意的$g_2\in R(K_1)$, 问题 (BP2) 的精确解为

如果 $\kappa_2\neq\emptyset$, 那么对任意的 $g_2\in R(K_2)$, 积分方程 (3.8) 存在无穷多个解, 但在 $L^2(\Omega)$ 空间内只有一个最佳近似解

证 由积分方程(3.8)易得.

下一步, 给出初值 $\varphi(x)$ 和 $\psi(x)$ 的条件稳定性结果. 初值 $\varphi(x)$ 和 $\psi(x)$ 的先验界条件分别为

其中 $E_1$, $E_2$ 和 $ p $ 均是正常数.

定理3.3 如果 $\varphi(x)$ 满足先验界 $\|\varphi(\cdot)\|_{D(((-\Delta)^{\beta-\gamma})^{\frac{p}{2}})} \leq E_1$, 那么

其中 $C_{5}=(C_1)^{-\frac{p}{p+2}}$.

由 Hölder 不等式可得

根据引理 2.5 和先验界 (3.21) 时可得

结合(3.24)和(3.25)式有(3.23)式. 证毕.

定理3.4 如果 $\psi(x)$ 满足先验界 $\|\psi(\cdot)\|_{D(((-\Delta)^{\beta-\gamma})^{\frac{p}{2}})} \leq E_2$, 那么

其中 $C_{6}=(C_1T)^{-\frac{p}{p+2}}$.

本节中, 将使用 Tikhonov 正则化方法来解决不适定问题 (BP1) 和 (BP2), 并分别给出它们的精确解与正则解在先验正则化参数选取规则和后验正则化参数选取规则下的收敛误差估计.

对于不适定问题 (BP1) 和 (BP2), 它们的极小化 Tikhonov 泛函分别为

其中 $\mu_1>0$ 和 $\mu_2>0$ 为正则化参数. 根据文献[35] 的定理5.1可知, 在 $L^2(\Omega)$ 上存在唯一的极小元 $\varphi_{\mu_1}$ 和 $\psi_{\mu_2}$ 分别满足

带入算子 $K_1$ 和 $K_2$ 的奇异值, 不带误差的正则解为

带误差的正则解为

其中

定理4.1 如果先验界(3.21)式和误差假设(1.2)成立, 那么

(1) 当 $0<p< 4$ 时, 取正则化参数 $\mu_1=(\frac{\delta}{E_1})^{\frac{4}{p+2}}$, 误差估计为

(2) 当 $p \geq 4$ 时, 取正则化参数 $\mu_1=(\frac{\delta}{E_1})^{\frac{2}{3}}$, 误差估计为

其中$C_{11}:=(4-p)^{\frac{4-p}{4}}p^{\frac{p}{4}}C_1^{-\frac{p}{2}}$, $C_{12}:=\frac{1}{C_{1}^{2}\lambda_{1}^{\frac{p}{2}-2}}$.

证 利用三角不等式

首先, 对(4.11)式右端的第一项进行估计. 通过(4.5),(4.7)和(1.2)式可得

即

下面, 对(4.11)式右端的第二项进行估计. 由(3.18),(3.21),(4.5)式和引理 2.5 可得

其中 $A_1(j)=\frac{\mu_1\lambda_{j}^{(2-\frac{p}{2})(\beta-\gamma)}}{(C_1)^2+\mu_1\lambda_{j}^{2(\beta-\gamma)}}$.

令 $s=\lambda_{j}^{\beta-\gamma}$. 利用引理 2.6 可得

其中$C_{11}:=(4-p)^{\frac{4-p}{4}}p^{\frac{p}{4}}C_1^{-\frac{p}{2}}$, $C_{12}:=\frac{1}{C_{1}^{2}\lambda_{1}^{\frac{p}{2}-2}}$.

故有

结合(4.12)和(4.14)式有

选取正则化参数为 $\mu_1 = (\frac{\delta}{E_1})^{\frac{4}{p+2}}(0 < p <4)$ 和 $\mu_1 = (\frac{\delta}{E_1})^{\frac{2}{3}}(p \geq4)$, 则

证毕.

本节中, 将通过 Morozov 不一致原理选出正则化参数, 从而给出 $\|\varphi_{\mu_1}^{\delta}(\cdot)-\varphi(\cdot)\|$ 的后验误差估计. Morozov 不一致原理如下

其中 $\tau_1>1$ 是常数, 且 $\|g_{1}^{\delta}\| > \tau_1\delta$.

引理4.1 设 $\rho({\mu_1}):=\|K_1\varphi_{\mu_1}^{\delta}(x)-g_{1}^{\delta}\|$, 有以下结论

(a) $\rho(\mu_1)$ 是连续函数;

(b) $\lim\limits_{\mu_1\rightarrow0}\rho(\mu_1)=0;$

(c) $\lim\limits_{\mu_1\rightarrow+\infty}\rho(\mu_1)=\|g_{1}^{\delta}(\cdot)\|;$

(d) $\rho(\mu_1)$ 在 $\mu_1\in(0,+\infty)$ 上是严格单调递增的.

证 以上性质可由 $\rho(\mu_1)$ 的表达式直接推导得出

证毕.

定理4.2 如果先验界条件 $(3.21)$ 和误差假设 $(1.2)$ 成立. $\tau_1>1$, 正则化参数 $\mu_1$ 由 $(4.17)$ 式选出, 则

(1) 当 $0 < p < 2$ 时, 误差估计为

(2) 当 $p \geq2$ 时, 误差估计为

其中 $C_{21}:=(2-p)^{\frac{2-p}{4}}(2+p)^{\frac{2+p}{4}}C_{1}^{-\frac{2+p}{2}}$, $C_{22}:=C_{1}^{-2}\lambda_{1}^{1-\frac{p}{2}} $.

证 由三角不等式得

首先, 对(4.20)式右端的第一项进行估计. 由(4.12)式可知

通过(4.17)和(1.2)式得

其中 $A_2(j)=\frac{\mu_1C_2\lambda_{j}^{(1-\frac{p}{2})(\beta-\gamma)}}{C_{1}^{2}+\mu_1\lambda_{j}^{2(\beta-\gamma)}}$.

令 $s=\lambda_{j}^{\beta-\gamma}$, 使用引理 2.7 可得

故有

因此

将(4.24)式代入(4.21)式可得

下一步, 对(4.20)式右端的第二项进行估计. 由(4.17)式和 $\varphi(x)$ 的先验界条件可得

利用条件稳定性可得

即

结合(4.20),(4.25)和(4.26)式

证毕.

定理4.3 如果先验界 $(3.22)$ 式和误差假设 $(1.2)$ 成立, 那么

(1) 当 $0<p< 4$ 时, 取正则化参数 $\mu_2=(\frac{\delta}{E_2})^{\frac{4}{p+2}}$, 误差估计为

(2) 当 $p \geq 4$ 时, 取正则化参数 $\mu_2=(\frac{\delta}{E_2})^{\frac{2}{3}}$, 误差估计为

其中$C_{11}:=(4-p)^{\frac{4-p}{4}}p^{\frac{p}{4}}(C_1T)^{-\frac{p}{2}}$, $C_{12}:=\frac{1}{(TC_{1})^{2}\lambda_{1}^{\frac{p}{2}-2}}$.

证 该证明与定理 4.1 同理, 故省略.

下面给出将通过以下 Morozov 不一致原理选取正则化参数 $\mu_2$,

其中 $\tau_2>1$ 是常数, $\|g_{2}^{\delta}\| > \tau_2\delta$.

引理4.2 令 $\rho({\mu_2}):=\|K_2\psi_{\mu_2}^{\delta}(x)-g_{2}^{\delta}\|$, 有以下性质

a) $\rho(\mu_2)$ 是连续函数;

b) $\lim\limits_{\mu_2\rightarrow0}\rho(\mu_2)=0;$

c) $\lim\limits_{\mu_2\rightarrow+\infty}\rho(\mu_2)=\|g_{2}^{\delta}(\cdot)\|;$

d) $\rho(\mu_2)$ 在 $\mu_2\in(0,+\infty)$ 上是严格单调递增函数.

证 该证明与引理 4.1 同理, 故省略.

定理4.4 如果先验界(3.22)式和误差假设(1.2)成立, $\tau_2>1$, 正则化参数 $\mu_2$ 由(4.30)式选出, 那么

(1) 当 $0 < p < 2$ 时, 误差估计为

(2) 当 $p \geq2$ 时, 误差估计为

其中 $C_{21}:=(2-p)^{\frac{2-p}{4}}(2+p)^{\frac{2+p}{4}}(TC_{1})^{-\frac{2+p}{2}}$, $C_{22}:=\frac{1}{(TC_{1})^{2}\lambda_{1}^{\frac{p}{2}-1}}$.

证 该证明与定理 4.2 同理, 故省略.

本节主要是通过给定数值算例来说明 Tikhonov 正则化方法的有效性和稳定性. 以下数值模拟包含两部分, 第一部分: 给定初值 $\varphi(x)$ 和 $\psi(x)$, 求一个正问题, 从而得到终值数据 $g(x)$. 第二部分: 通过对终值数据 $g(x)$ 增加扰动来得到测量数据 $g^{\delta}(x)$, 再利用测量数据 $g^{\delta}(x)$ 来反演初值 $\varphi(x)$ 和 $\psi(x)$.

令 $\gamma=0.5$, $\beta=1$, $v=1$, $\Omega=(0,\pi)$, $T=1$. 考虑以下一维正问题

通过有限差分方法对上述方程进行离散. 将时间 $[01]$ 作 $N$ 等分, 空间 $[\pi]$ 作 $M$ 等分, 时间和空间步长分别为 $\Delta t=\frac{T}{N}$ 和 $\Delta x=\frac{\pi}{M}$, $t_{n}=n\Delta t$$(n = 0,1,\cdots, N)$, $x_{i}=i \Delta x$$(i = 0,1, \cdots, M)$. $u_{i}^{n}=u(x_i,t_n)$$(n = 0,1,\cdots, N;i = 0,1, \cdots, M)$ 是网格点上的值.

Caputo 分数阶导数的离散差分格式如下^[36]

其中 $i=1,\cdots,M-1$; $n=1,\cdots,N$, $b_{j}=(j+1)^{2-\alpha}-j^{2-\alpha}$. 分数阶 Laplace 算子为$(-\Delta)^s=-\frac{\partial^{2s}}{\partial x^{2s}}$.

设

有以下迭代格式

其中 $A$ 是三对角矩阵,

其中

通过 MATLAB 软件编程对上述差分格式进行求解, 可得到终值数据 $g(x)$ 的值. 下一步, 将对该问题的反问题进行求解.

由于实践中, 先验界很难得到, 而先验正则化参数的选取又基于先验界条件, 所以在该数值模拟中, 只给出在后验正则化参数选取规则下的数值结果. 下面通过对精确数据 $g(x)$ 添加一个随机干扰产生噪声数据 $g^{\delta}(x)$

其中函数 randn($\cdot$) 产生一个均值为0, 方差为1的随机数列.

$\varphi(x)$ 和 $\psi(x)$ 的相对误差 $\varepsilon_1$ 和 $\varepsilon_2$ 分别由下式给出

误差水平 $\delta$ 由下式给出

取 $M=100$, $N=100$, 令 (4.17) 式中的 $\tau_{1}=1.1$ 和 (4.30) 式中的 $\tau_{2}=1.1$. 当反演初值 $\varphi(x)$ 时, 令 $\psi(x)=\sin(4\pi x)$. 当反演初值 $\psi(x)$ 时, 令 $\varphi(x)=x\sin(x)$. 下面给出六个数值算例.

例 1 考虑光滑函数

例 2 考虑分段光滑函数

例 3 考虑分段光滑函数

例 4 考虑光滑函数

例 5 考虑分段函数

例 6 考虑分段函数

图 1 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 光滑函数例 1 的精确解 $\varphi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\varphi_{\mu_1}^{\delta}(x)$ 之间的比较. 图 2 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 分段光滑函数例 2 的精确解 $\varphi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\varphi_{\mu_1}^{\delta}(x)$ 之间的比较. 图 3 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 分段光滑函数例 3 的精确解 $\varphi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\varphi_{\mu_1}^{\delta}(x)$ 之间的比较.

图 4 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 光滑函数例 4 的精确解 $\psi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\psi_{\mu_2}^{\delta}(x)$ 之间的比较. 图 5 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 分段函数例 5 的精确解 $\psi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\psi_{\mu_2}^{\delta}(x)$ 之间的比较. 图 6 为 $\alpha$ 分别取 $1.3$, $1.5$, $1.7$ 时, 分段函数例 6 的精确解 $\psi(x)$ 与 $\varepsilon $ 分别取 $0.01$, $0.001$, $0.0001$ 时的 Tikhonov 正则解 $\psi_{\mu_2}^{\delta}(x)$ 之间的比较. 表 1比较了例 1-6 在不同 $\alpha$ 和 $\varepsilon$ 取值情况下精确解与 Tikhonov 正则解之间的相对误差.

从 图 1-6 可以看出 Tikhonov 正则化方法可以恢复解的稳定性. 结合 图 1-6 和 表 1 可以看出当 $\alpha$ 越小, $\varepsilon$ 越小时, 精确解与 Tikhonov 正则解之间的相对误差越小, 数值图像效果越好, 且光滑函数比非光滑函数的数值反演效果更好.

本文研究时空分数阶扩散波动方程的初值识别问题, 该问题是不适定的. 采用 Tikhonov 正则化方法对两个初值 $\varphi(x)$ 和 $\psi(x)$ 分别进行正则化, 并分别给出初值 $\varphi(x)$ 和 $\psi(x)$ 在先验和后验正则化参数选取规则下的收敛误差估计. 由先验和后验误差估计式可知 Tikhonov 正则化方法具有饱和效应. 最后, 从数值结果可以看出随着 $\alpha$ 和 $\varepsilon$ 越小, 数值结果越好, 所以 Tikhonov 正则化方法是有效的.