数学物理学报 ›› 2023, Vol. 43 ›› Issue (2): 377-398.
时空分数阶扩散波动方程的初值识别问题
- 兰州理工大学理学院 兰州 730050
-
收稿日期:2022-02-18修回日期:2022-10-17出版日期:2023-04-26发布日期:2023-04-17 -
通讯作者:杨帆,E-mail:yfggd114@163.com -
基金资助:国家自然科学基金(11961044);兰州理工大学博士基金和甘肃省自然科学基金(21JR7RA214)
Identification of Initial Values of Space-Time Fractional Diffusion-Wave Equation
Yang Fan*( ),Cao Ying,Li Xiaoxiao
),Cao Ying,Li Xiaoxiao
- School of Science, Lanzhou University of Technology, Lanzhou 730050
-
Received:2022-02-18Revised:2022-10-17Online:2023-04-26Published:2023-04-17 -
Supported by:NSFC(11961044);Doctor Fund of Lanzhou University of Techonology and the NSF of Gausu Province(21JR7RA214)
摘要:
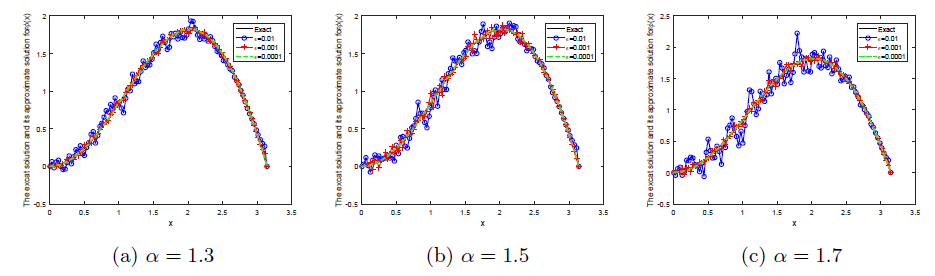
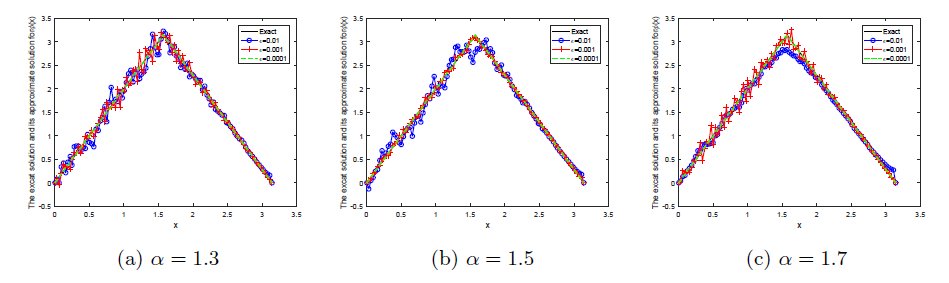
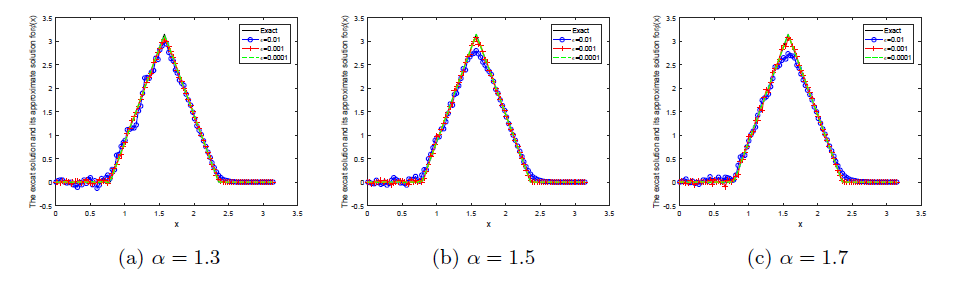
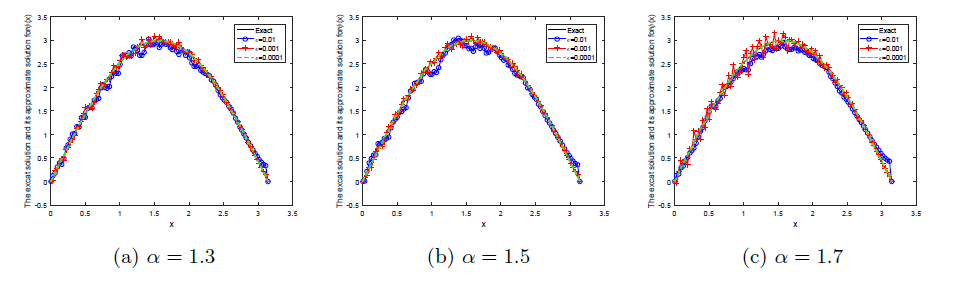
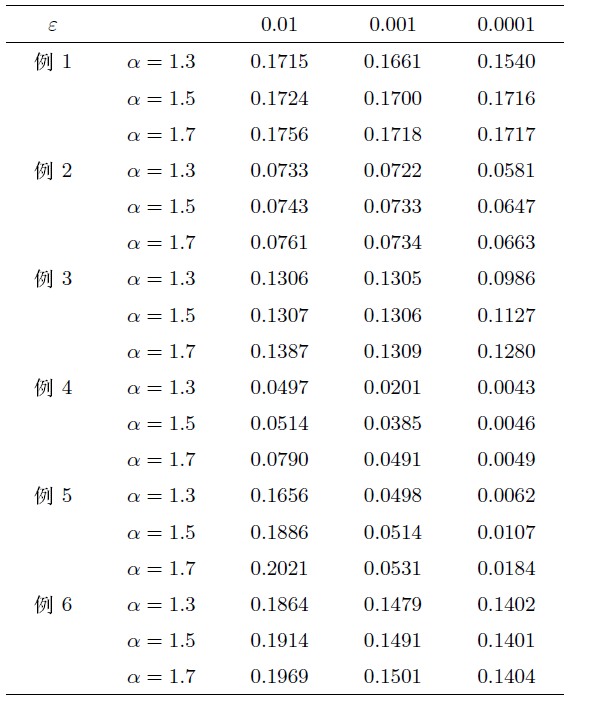
研究具有时空分数阶导数的扩散波动方程的初值识别反问题. 分析该反问题的不适定性, 给出条件稳定性结果. 利用 Tikhonov 正则化方法恢复解的稳定性, 并分别给出在先验和后验正则化参数选取规则下, 正则解和精确解之间的误差估计. 通过数值算例说明 Tikhonov 正则化方法求解此类反问题非常有效.
中图分类号:
- O175
引用本文
杨帆, 曹英, 李晓晓. 时空分数阶扩散波动方程的初值识别问题[J]. 数学物理学报, 2023, 43(2): 377-398.
Yang Fan, Cao Ying, Li Xiaoxiao. Identification of Initial Values of Space-Time Fractional Diffusion-Wave Equation[J]. Acta mathematica scientia,Series A, 2023, 43(2): 377-398.
使用本文
| [1] | Podlubny I. Fractional Differential Equations. New York: Academic Press, 1999 |
| [2] | Samko S G, Kilbas A A, Marichev O I. Fractional Integrals and Derivatives: Theory and Applications. Switzerland: Gordon and Breach, 1993 |
| [3] | Odzijewicz T, Malinowska A B, Torres D F M. Fractional calculus of variations in terms of a generalized fractional integral with applications to physics. Abstr Appl Anal, 2012, 2012(2): 919-929 |
| [4] |
Herrmann R. Common aspects of q-deformed Lie algebras and fractional calculus. Physica A, 2010, 389(21): 4613-4622
doi: 10.1016/j.physa.2010.07.004 |
| [5] | Millerand K, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: Wiley, 1993 |
| [6] |
Giona M, Cerbelli S, Roman H E. Fractional diffusion matrix and relaxation in complex viscoelastic materials. Physica A, 1992, 191(1-4): 449-453
doi: 10.1016/0378-4371(92)90566-9 |
| [7] |
Roman H E, Alemany P A. Continuous-time random walks and the fractional diffusion matrix. J Phys A-Math Gen, 1994, 27( 10): 3407
doi: 10.1088/0305-4470/27/10/017 |
| [8] |
Berkowitz B, Scher H, Silliman S E. Anomalous transport in laboratory-scale, heterogeneous porous media. Water Resour Res, 2000, 36(1): 149-158
doi: 10.1029/1999WR900295 |
| [9] | Ba Y, Jiang L, Ou N. A two-stage ensemble Kalman filter based on multiscale model reduction for inverse problems in time fractional diffusion-wave matrixs. J Comput Phys, 2018, 374: 300-330 |
| [10] |
Agrawal O P. Solution for a fractional diffusion-wave matrix defined in a bounded domain. Nonlinear Dynam, 2002, 29(1): 145-155
doi: 10.1023/A:1016539022492 |
| [11] |
Chen A, Li C. Numerical solution of fractional diffusion-wave matrix. Numer Funct Anal Optim, 2016, 37(1): 19-39
doi: 10.1080/01630563.2015.1078815 |
| [12] | Jiang H, Liu F, Turner I, et al. Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion matrixs in a finite domain. Comput Math Appl, 2012, 64(10): 3377-3388 |
| [13] | Lopushansky A, Lopushansky O, Sharyn S. Nonlinear inverse problem of control diffusivity parameter determination for a space-time fractional diffusion matrix. Appl Math Comput, 2021, 390: 125589 |
| [14] | Yang F, Zhang Y, Liu X, et al. The quasi-boundary value method for identifying the initial value of the space-time fractional diffusion matrix. Acta Math Sci, 2020, 40B(3): 641-658 |
| [15] | Tatar S, Tinaztepe R, Ulusoy S. Determination of an unknown source term in a space-time fractional diffusion matrix. J Fract Calc Appl, 2015, 6(1): 83-90 |
| [16] | Tuan N H, Long L D. Fourier truncation method for an inverse source problem for space-time fractional diffusion matrix. Electron J Differ Eq, 2017, 122: 1-16 |
| [17] | Zhang Y X, Jia J, Yan L. Bayesian approach to a nonlinear inverse problem for a time-space fractional diffusion matrix. Inverse Probl, 2018, 34( 12): 125002 |
| [18] | Tatar S, Ulusoy S. A uniqueness result for an inverse problem in a space-time fractional diffusion matrix. Electron. J Differ Equ, 2013, 257: 1-9 |
| [19] |
Tatar S İ, Tınaztepe R, Ulusoy S. Simultaneous inversion for the exponents of the fractional time and space derivatives in the space-time fractional diffusion matrix. Appl Anal, 2016, 95(1): 1-23
doi: 10.1080/00036811.2014.984291 |
| [20] |
Tatar S, Ulusoy S. An inverse source problem for a one-dimensional space-time fractional diffusion matrix. Appl Anal, 2015, 94(11): 2233-2244
doi: 10.1080/00036811.2014.979808 |
| [21] | Jin B, Rundell W. A tutorial on inverse problems for anomalous diffusion processes. Inverse probl, 2015, 31( 3): 035003 |
| [22] | Tuan N A, O'Regan D, Baleanu D, et al. On time fractional pseudo-parabolic matrixs with nonlocal integral conditions. Evol Equ Control The, 2022, 11(1): 225-238 |
| [23] |
Liao K F, Li Y S, Wei T. The identification of the time-dependent source term in time-fractional diffusion-wave matrixs. East Asian J Appl Math, 2019, 9(2): 330-354
doi: 10.4208/eajam |
| [24] |
Yan X B, Wei T. Determine a space-dependent source term in a time fractional diffusion-wave matrix. Acta Appl Math, 2020, 165(1): 163-181
doi: 10.1007/s10440-019-00248-2 |
| [25] | Wei T, Yan X. Recovering a space-dependent source term in a time-fractional diffusion wave matrix. J Appl Anal Comput, 2019, 9(5): 1801-1821 |
| [26] | Yan X, Zhang Z, Wei T. Simultaneous inversion of a time-dependent potential coefficient and a time source term in a time fractional diffusion-wave matrix. Chaos Soliton Fract, 2022, 157: 111901 |
| [27] | Xian J, Wei T. Determination of the initial data in a time-fractional diffusion-wave problem by a final time data. Comput Math Appl, 2019, 78(8): 2525-2540 |
| [28] | Yang F, Sun Q X, Li X X. Three Landweber iterative methods for solving the initial value problem of time-fractional diffusion-wave matrix on spherically symmetric domain. Inverse Probl Sci En, 2021, 29(12): 2306-2356 |
| [29] | Wei T, Zhang Y. The backward problem for a time-fractional diffusion-wave matrix in a bounded domain. Comput Math Appl, 2018, 75(10): 3632-3648 |
| [30] |
Yang F, Pu Q, Li X X, et al. The truncation regularization method for identifying the initial value on non-homogeneous time-fractional diffusion-wave matrixs. Mathematics, 2019, 7( 11): 1007
doi: 10.3390/math7111007 |
| [31] | Jiang S Z, Wu Y J. Recovering space-dependent source for a time-space fractional diffusion wave matrix by fractional Landweber method. Inverse Probl Sci En, 2021, 29(7): 990-1011 |
| [32] |
Yang F, Zhang Y, Li X X. Landweber iterative method for identifying the initial value problem of the time-space fractional diffusion-wave matrix. Numer Algorithms, 2020, 83(4): 1509-1530
doi: 10.1007/s11075-019-00734-6 |
| [33] |
Chen W, Li C. Maximum principles for the fractional p-Laplacian and symmetry of solutions. Adv Math, 2018, 335: 735-758
doi: 10.1016/j.aim.2018.07.016 |
| [34] | Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier, 2006 |
| [35] | Engl H W, Hanke M, Neubauer A. Regularization of Inverse Problem. Dordrecht: Kluwer Academic Publishers, 1996 |
| [36] | Sun Z. The Method of Order Reduction and Its Application to the Numerical Solutions of Partial Differential Equations. Beijing: Science Press, 2009 |
| [1] | 王克彦,王奇生. 一类非线性双曲型方程扩展混合有限元方法的误差估计[J]. 数学物理学报, 2021, 41(2): 468-478. |
| [2] | 赵振宇,林日光,李志,梅端. 确定热方程未知源问题的超阶正则化方法[J]. 数学物理学报, 2020, 40(3): 717-724. |
| [3] | 杨朝强. 一类特殊混合跳扩散Black-Scholes模型的欧式回望期权定价[J]. 数学物理学报, 2019, 39(6): 1514-1531. |
| [4] | 葛志昊, 曹济伟. 反应扩散问题的新的绝对稳定hp间断Galerkin方法[J]. 数学物理学报, 2018, 38(2): 385-394. |
| [5] | 方志朝, 李宏, 罗振东, 刘洋. Sine-Gordon方程的混合有限体积元方法及数值模拟[J]. 数学物理学报, 2018, 38(2): 395-416. |
| [6] | 陈传军, 张晓艳, 赵鑫. 一维非线性抛物问题两层网格有限体积元逼近[J]. 数学物理学报, 2017, 37(5): 962-975. |
| [7] | 谢瓯, 孟泽红, 赵振宇, 由雷. 求解拉普拉斯方程柯西问题的截断赫尔米特展开方法[J]. 数学物理学报, 2017, 37(3): 457-468. |
| [8] | 杨帆, 傅初黎, 李晓晓, 任玉鹏. 一类非线性反向热传导问题的Fourier正则化方法[J]. 数学物理学报, 2017, 37(1): 62-71. |
| [9] | 陈传军, 赵鑫. 一类非线性对流扩散方程两重网格特征有限元方法及误差估计[J]. 数学物理学报, 2014, 34(3): 643-654. |
| [10] | 赵振宇, 由雷. 求解热源识别问题的修正吉洪诺夫正则化方法[J]. 数学物理学报, 2014, 34(1): 186-192. |
| [11] | 石东洋, 于志云. 带有阻尼项的定常Stokes方程的低阶非协调混合有限元方法的超逼近和超收敛分析[J]. 数学物理学报, 2013, 33(4): 735-745. |
| [12] | 方志朝, 李宏, 罗振东. 伪双曲型方程的混合控制体积方法[J]. 数学物理学报, 2013, 33(3): 535-550. |
| [13] | 李磊, 孙萍, 罗振东. 抛物方程一种新混合有限元格式及误差分析[J]. 数学物理学报, 2012, 32(6): 1158-1165. |
| [14] | 何斯日古楞, 李宏. 弹性动力学问题的混合间断时空有限元法[J]. 数学物理学报, 2012, 32(6): 1179-1190. |
| [15] | 石东洋, 裴丽芳, 许超. 双负介质中电磁波传播的各向异性非协调有限元分析[J]. 数学物理学报, 2012, 32(5): 982-995. |
|