1 引言
令 \Omega \Bbb R^N (N\geq 2)
\begin{equation} \label{MA} M[u]=K(x)f(u),\ x\in \Omega,\; u= +\infty\ \mbox{在 $\partial \Omega$上 }, \end{equation}
(1.1)
其中 M[u]=\det\, (u_{x_{i}x_{j}}) \partial\Omega u=+\infty {\rm dist}(x,\partial\Omega)\to 0
\mbox{ $u(x)\to+\infty$}.
(K) K\in C^\infty(\Omega) \Omega K(x)>0
(f) 存在 \eta\in \Bbb R^1\cup\{-\infty\},
(i) f\in C^{\infty}(\eta,\infty) (\eta,\infty)
(ii) 如果 \eta\in\Bbb R^1 f(\eta):=\lim\limits_{s\rightarrow \eta}f(s)=0 .
我们不仅讨论对 K(x) f(u)
据我们所知, 边界爆破解是由 Bieberbach[1 ] 率先进行了研究. 确切地说, Bieberbach[1 ] 研究了如下N=2
\begin{equation} \label{Lp} \left\{\begin{array}{ll} \Delta u=K(x)f(u), \ &x\in \Omega,\;\\ u= +\infty, \ &x\in \partial \Omega, \end{array}\right. \end{equation}
(1.2)
其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] .
特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
\begin{equation} \label{suf} \Psi(s)=\int_{s}^\infty [(N+1)F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty,\forall s>\eta, \end{equation}
(1.3)
\begin{equation} \label{nec} \int_{1}^\infty f(s)^{-1/N}{\rm d}s=\infty, \end{equation}
(1.4)
\mbox{当}\ \eta\in\Bbb R^1 \ \mbox{时},\ F(s)=\int_\eta^sf(t){\rm d}t; \ \mbox{当 }\ \eta=-\infty \ \mbox{时},\ F(s)=\int_0^s f(t){\rm d}t.
众所周知, 当 K\in C^\infty(\overline \Omega)>0 f(u)=u^p f(u)={\rm e}^u [31 ] 证明了: 如果 \eta>-\infty f(u)=u^p f(u)={\rm e}^u
\begin{equation} \label{extra} \int_{\eta^+}[(N+1)F(s)]^{-1/(N+1)}{\rm d}s=\infty. \end{equation}
(1.5)
这里 \int_{\eta^+}\Phi(s){\rm d}s=\infty \epsilon
\int_\eta^{\eta+\epsilon}\Phi(s){\rm d}s=\infty.
显然,(1.5)式等价于 \lim\limits_{s\to \eta^+}\Psi(s)=\infty. [31 ] , 或者 p - Laplacian 方程[21 ] (在这种情况下(1.5)式变为 \int_{\eta^+}[F(s)]^{-1/p}{\rm d}s=\infty ).
同时, 在文献[31 ,定理 1.1]中, Zhang 和 Du[31 ] 还证明了, 如果 K\in C^\infty(\overline \Omega)>0 f
当 K\in C^\infty(\overline \Omega)>0 \eta\in\Bbb R^1 33 ] 中, Zhang 和 Feng 研究了 k - Hessian 方程 (当 k=N I(s)
I(s)=\frac{\Psi''(s)\Psi(s)}{(\Psi'(s))^2},
其中, 当 k=N \Psi
I_{\eta}=\lim\limits_{s\to \eta^{+}}I(s)\neq\infty\ (\eta\in\Bbb R^1),
那么问题(1.1)存在一个严格解 u 0<c_{2}<c_{1} u
\begin{equation}\label{1.11}\psi(c_{1}d(x))\leq u(x)\leq \psi(c_{2}d(x)), x\in \Omega,\end{equation}
(1.6)
其中 \psi \Psi [17 ] 和 Matero[18 ] 还得到了全局估计(1.6)式. 由下面的定理 3.2 知 I_\eta\neq \infty
对于一般形式的 K(x) [19 ] 指出如果 K(x)
\begin{equation} \label{K} M[u]=K(x),\ x\in \Omega,\; u=0,\ x\in \partial \Omega \end{equation}
(1.7)
有一个严格凸解, 那么问题(1.1)有一个严格凸解的条件是 f \eta\in\Bbb R^1 32 ] 中, Zhang 和 Feng 证明了(1.3)式 (如果 \eta\in\Bbb R^1
由文献[4 ,定理1.1]知, 如果 K\in C^\infty(\overline \Omega) K(x) \partial\Omega
令 d(x):={\rm dist} (x,\partial\Omega) . 在文献[5 ]中, 对于某些 \delta>0 C>0 0<K(x)<Cd(x)^{\delta-N-1}\ (x\in\Omega)
在文献[20 ] 中, 对于某些 C>0 K(x)\geq Cd(x)^{-N-1}\ (x\in\Omega) [30 ] 推广了这些结果. 当 K(x)
(i) 对于某些 C>0 \partial\Omega K(x)\geq Cd(x)^{-N-1}(-\ln d(x))^{-N}
(ii) 对于某些 q>N C>0 \partial\Omega K(x)\leq Cd(x)^{-N-1}(-\ln d(x))^{-q}
下面, 我们介绍 Zhang 和 Du[31 ] 得到的一个结果. 在这个结果中, 他们对于 K(x) [30 ] 提出的条件更具有一般性.
令 p(t)\in C^1(0,\infty)
p'(t)<0,\ \lim_{t\to 0^+}p(t)=+\infty.
为了区分其在t=0 P(\tau)=\int_{\tau}^{1}p(t){\rm d}t . 如果
\begin{equation} \label{P_inftyp} \int_{0^+}[P(\tau)]^{\frac{1}{N}}{\rm d}\tau<\infty, \end{equation}
(1.8)
那么我们称 p(t) {\cal P}_{finite}
\int_{0^+}[P(\tau)]^{\frac{1}{N}}{\rm d}\tau=\infty,
那么我们称 p(t) {\cal P}_\infty
定理 1.1 (Zhang 和 Du[31 ,定理 1.5] ) 令 K
(i) 如果存在一个 {\cal P}_\infty p(t) \partial \Omega K(x)\geq p(d(x))
(ii) 如果存在一个 {\cal P}_{finite} p(t) \partial \Omega K(x)\leq p(d(x))
\begin{equation} \label{omega} \omega_0(t):=\int_{0}^{t}(NP(\tau))^{\frac{1}{N}}{\rm d}\tau,\ \ \forall t\in (0,b), \end{equation}
(1.9)
那么问题(1.7)有一个严格凸解 u\in C^{\infty}(\Omega)\cap C(\overline\Omega)
\begin{equation} \label{u_0} -l_{0}\,\omega_0(d(x))\leq u(x)<0,\ \ \forall x\in \Omega, \end{equation}
(1.10)
注 1.1 Zhang 和 Du[31 ] 中对函数 p(t) p(t)
\begin{equation} \label{P_infty1} \int_{0^+}[p(\tau)]^{\frac{1}{N+1}}{\rm d}\tau<\infty. \end{equation}
(1.11)
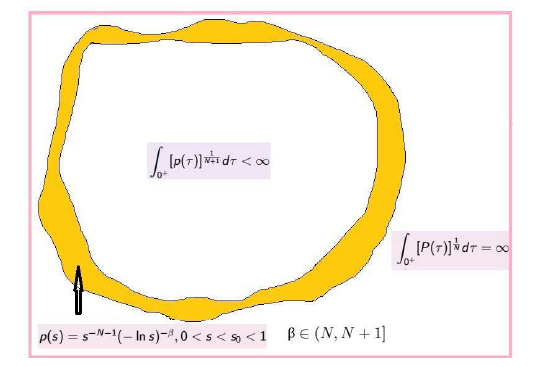
p(t)=t^{-N-1}(-\ln t)^{-\beta}, 0<t<t_{0}<1,\ \beta\in (N,N+1],
\int_{0^+}[P(\tau)]^{\frac{1}{N}}{\rm d}\tau<\infty,\ i.e. \ p\in P_{finite},
\int_{0^+}[p(\tau)]^{\frac{1}{N+1}}{\rm d}\tau=\infty.
这表明条件(1.11)比条件(1.8)强. 条件(1.8)和条件(1.11)之间的关系由下图1 给出.
图1
对充分大的 t p(t) c_0 t t\geq M_0 ) , 令 p(t)=c_0{\rm e}^{-t} . 对这样的 p(t)
\tilde P(\tau)=\int_\tau^\infty p(t){\rm d}t,
\begin{equation} \label{P_infty} \int_{0^+}[\tilde P(\tau)]^{\frac1N}{\rm d}\tau<\infty. \end{equation}
(1.12)
\begin{equation} \label{P/p} \tilde P(t)=c_0{\rm e}^{-t},\; \tilde P(t)/p(t)=1,\ \ \forall t\geq M_0,\ \mbox{且当}\ t\to 0 \ \mbox{时},\ \tilde P(t)/p(t)\to 0. \end{equation}
(1.13)
\begin{equation} \label{omega-1} \omega(t):=\int_{0}^{t}(N\tilde P(\tau))^{\frac{1}{N}}{\rm d}\tau,\ \ \forall\ t>0. \end{equation}
(1.14)
\begin{equation} \label{1.13}J(s)=-\frac{\omega(s)\omega''(s)}{(\omega'(s))^2}.\end{equation}
(1.15)
假设 \lim\limits_{s\rightarrow 0^{+}}J(s) J_{0}
如果假设 f K {\cal P}_{finite} p(t) K(x)\sim p(d(x)) J_{0}\neq 0 33 ,定理 1.5] (当 k=N 0<c_{2}<c_{1} u
\begin{equation} \label{1-14}\psi(c_{1}[\omega(d(x))]^{\frac{N}{N+1}})\leq u(x)\leq \psi(c_{2}[\omega(d(x))]^{\frac{N}{N+1}}), x\in \Omega.\end{equation}
(1.16)
p(t)=t^{\sigma}(\sigma>-1-N),\ \ \ p(t)=t^{-N-1}(-\ln t)^{-q}(q>N)
最近, Zhang[34 ] 得到了严格凸解的最优的全局估计和边界渐近行为. 作者对 f
\begin{equation} \label{onf} \Gamma(s)=\int_{s}^\infty [Nf(\tau)]^{-1/N}{\rm d}\tau<\infty,\forall s>\eta. \end{equation}
(1.17)
\begin{equation}\label{1-16}I_1(s)=\frac{\Gamma''(s)\Gamma(s)}{(\Gamma'(s))^2}.\end{equation}
(1.18)
关于 f K [34 ] 获得的主要结果是: 证明了问题(1.1)存在严格凸解, 并且有下面的全局渐近性质
\begin{equation} \gamma(c_{1}[\omega(d(x))]^{\frac{N}{N+1}})\leq u(x)\leq \gamma(c_{2}[\omega(d(x))]^{\frac{N}{N+1}}), x\in \Omega,\end{equation}
(1.19)
其中, \gamma(s) \Gamma(s)
接下来有一个自然的问题:如果 K(x) f [31 ] 仅考虑了径向对称的情况, 在 f \Omega
由上面的文献可知, 如果 K\in C^\infty(\overline \Omega) \Psi,\ \Gamma,\ I_{\eta},\ I_{1\eta},
\int_{\eta^+}[F(s)]^{-1/(N+1)}{\rm d}s,\ \int_{\eta^{+}}[f(s)]^{-1/N}{\rm d}s
在研究严格凸解的存在性和渐近行为是起着重要作用. 事实上, 当 K \partial\Omega \omega J_{0}
由文献[31 ,定理 4.1]的证明可知: 如果 \eta=-\infty \eta\in \Bbb R f(t+\eta) f(t) u-\eta u \eta=0 . 因此, 在本文我们仅仅考虑 \eta=0
论文的其余部分做如下安排. 在第二部分, 我们将引入 Karamata 正规变化理论并且回顾一些下文证明中要用到的结论. 第三部分致力于对 \Psi,\ \Gamma,\ I_{\eta},\ I_{1\eta}
\int_{\eta^+}[F(s)]^{-1/(N+1)}{\rm d}s,\ \int_{\eta^{+}}[f(s)]^{-1/N}{\rm d}s
进行比较. 在第四部分, 我们将对上述文献的一些定理进行比较, 寻找条件和估计之间的关系. 在第五部分, 我们在 K(x)
2 Karamata 正规变化理论
在这一节, 我们将回顾和 Karamata 正规变化理论相关的概念和结论, 详细内容请见参考文献[2 ,15 ,26 ]. 另外, 我们还将研究 I_{0}, I_{\infty}, I_{10} I_{1\infty}
定义2.1 对于 A>0 f [A,\infty) \xi>0
\begin{equation} \lim_{s\to \infty} \frac{f(\xi s)}{f(s)}=\xi^\rho, \end{equation}
(2.1)
其中 \rho\in R f f \in RV_{\rho} .
一般地, 当 \rho=0 f f \in RV_\rho L(s)=\frac{f(s)}{s^\rho}
定义2.2 对于 A>0 f [A,\infty) \rho>1
\begin{equation} \lim_{s\to \infty}\frac{f(s)}{s^\rho}=\infty, \end{equation}
(2.2)
命题2.1 (一致收敛定理) 令 f \in RV_\rho \xi \in [c_1,c_2] 0<c_1<c_2 \rho < 0 (c_{1}, \infty) c_{1} > 0 \rho > 0 f (0, c_{2}] (0, c_{2}] c_{2} > 0 .
命题2.2 (表示定理) 假设 A_1\geq A L L
L(s)=\psi(s)\exp\left(\int_{A_1}^s\frac{y(\tau)}{\tau}{\rm d}\tau\right),\ s\geq A_1,
其中 \psi y s \to \infty y(s)\to 0,\ \psi (s) \to c_0 c_0>0 .
有人称 \hat{L}(s)=c_0\exp\left(\int_{A_1}^s\frac{y(\tau)}{\tau}{\rm d}\tau\right) f(s)=s^\rho\hat{L}(s),\ s\geq A_{1}, f\in NRV_\rho .
不难看出, 当 s\rightarrow \infty L(s)\sim \hat {L}(s) .
\lim_{s\to \infty} \frac{sf'(s)}{f(s)}=\rho,
一个函数 f\in RV_\rho NRV_\rho f\in C^1[A_1,\infty).
命题2.4 如果函数 f, g L
1) f^p (p \in R),\ c_1f+c_2g(c_1,c_2 \ge 0) f\circ g s \to 0^+ g(s)\to 0)
2) 对每一个 \rho>0 s\to \infty s^{-\rho} L(s)\to 0,\ s^{\rho}L(s)\to \infty.
3) 对任意 \rho \in R s\to \infty \frac{\ln(L(s))}{\ln s} \to 0,\ \mbox{且}\ \frac{\ln (s^\rho L(s))}{\ln s} \to \rho.
命题2.5 如果 f_1\in RV_{\rho_1},\ f_2\in RV_{\rho_2}, f_1f_2\in RV_{\rho_1+\rho_2}, \ f_1 \circ f_2 \in RV_{\rho_1 \rho_2}.
命题2.6 (渐近行为) 如果一个函数 L a\geq 0 s\to \infty
1)\int_a^{t}s^\rho L(s){\rm d}s \cong (1+\rho)^{-1}t^{1+\rho}L(t),\ \forall\ \rho>-1;
2)\int_t^{\infty} s^\rho L(s){\rm d}s \cong (-1-\rho)^{-1}t^{1+\rho}L(t),\ \forall\ \rho<-1.
注2.1 当 t\rightarrow \infty
\frac{\int_a^{t}s^{-1} L(s){\rm d}s}{L(t)}\rightarrow \infty,
那么命题 2.6 对于 \rho=-1
命题 2.6 理解为 L(s) L(t) L(t)
\int_a^{t}s^\rho L(s){\rm d}s\sim L(t) \int_a^{t}s^\rho {\rm d}s (t\rightarrow \infty).
当 \rho=-1 z(s)=s^{-1}L(s)
命题2.7 (渐近行为[2 ,定理 1.5.9b]) 如果一个函数 z\in RV_{-1} \int_{s}^{\infty}z(\tau){\rm d}\tau<\infty, s>0, \int_{s}^{\infty}z(\tau){\rm d}\tau
\lim\limits_{s\to\infty}\frac{sz(s)}{\int_{s}^{\infty}z(\tau){\rm d}\tau}=0.
类似于定义 2.1, 2.2, 对于 a_{1} > 0, s\to 0^{+} s\to \infty (0, a_{1}) f 0 f \rho 0 f \in RVZ_{\rho} . 它也具有命题2.1 -命题2.7 的性质. 为了应用方便, 我们给出如下结果.
命题2.8 对于 s>0 z\in RV_{-1} \int_{s}^{a_{1}}z(\tau){\rm d}\tau<\infty, \int_{s}^{a_{1}}z(\tau){\rm d}\tau
\lim\limits_{s\to 0^{+}}\frac{sz(s)}{\int_{s}^{a_{1}}z(\tau){\rm d}\tau}=0.
证 证明过程类似于文献[2 ,定理 1.5.9 b]中的证明, 我们在这里省略掉证明过程.
给出一些在 0
(1) [\ln(1+x)]^\beta 0 \beta
(2) \frac{1}{\ln\frac{1}{x}} 0
(3) {\rm e}^{-\frac{1}{x}} 0
下面, 利用正规变化的理论, 我们证明 I(s) I_{1}(s)
\Psi'(s)=-[(N+1)F(s)]^{-\frac{1}{N+1}},
\Psi''(s)=[(N+1)F(s)]^{-\frac{1}{N+1}-1}f(s).
-\frac{1}{\Psi'(s)}=[(N+1)F(s)]^{\frac{1}{N+1}}.
I(s)=\frac{f(s)\Psi(s)}{[(N+1)F(s)]^{\frac{N}{N+1}}}.
假设极限 \lim\limits_{s\rightarrow \infty}I(s), \lim\limits_{s\rightarrow 0}I(s) I_{\infty} I_{0}
引理2.1 令 f \lim\limits_{s\rightarrow \infty}I(s), \lim\limits_{s\rightarrow 0}I(s)
I_{\infty}\ge 1,\ \ I_{0}\geq 1.
证 对 I(s) a(a>0) v
\begin{eqnarray*} \int_{a}^{v}I(s){\rm d}s&=&\int_{a}^{v}\frac{\Psi''(s)\Psi(s)}{(\Psi'(s))^2}{\rm d}s\\ &=&\int_{a}^{v}\frac{\Psi(s)}{(\Psi'(s))^2}{\rm d}\Psi'(s)\\ &=&\frac{\Psi(s)}{\Psi'(s)}\Big|_{a}^{v}-\int_{a}^{v}\frac{(\Psi'(s))^3-2\Psi(s)\Psi'(s)\Psi''(s)}{(\Psi'(s))^3}{\rm d}s\\ & =&\frac{\Psi(v)}{\Psi'(v)}-\frac{\Psi(a)}{\Psi'(a)}-v+a+2\int_{a}^{v}I(s){\rm d}s. \end{eqnarray*}
0\ge \lim\limits_{v\to \infty}\frac{\Psi(v)}{v\Psi'(v)}=1-\lim\limits_{v\to \infty}\frac{\int_{a}^{v}I(s){\rm d}s}{v}=1-\lim\limits_{v\to \infty}I(v)=1-I_{\infty},
即 I_{\infty}\ge 1. I_{0}\ge 1.
引理2.2 令 f \lim\limits_{s\rightarrow \infty}I(s)
(1) I_{\infty}\in (1,\infty) F\in NRV_{q+1}\ (q>N) . 从这个意义上说, f\in RV_{q}
(2) 如果 I_{\infty}=1 F
(3) 如果 F\in NRV_{N+1} I_{\infty}=\infty .
\begin{matrix}\label{3.6I} \lim\limits_{s\to \infty}\frac{-\frac{1}{\Psi'(s)}}{s(-\frac{1}{\Psi'(s)})'} &=&-\lim\limits_{s\to \infty}\frac{\frac{1}{\Psi'(s)}\Psi(s)}{s\frac{\Psi''(s)}{(\Psi'(s))^2}\Psi(s)} \\ & =&-\frac{1}{I_{\infty}}\lim\limits_{s\to \infty}\frac{\frac{\Psi(s)}{\Psi'(s)}}{s} \\ & =&-\frac{1}{I_{\infty}}\lim\limits_{s\to \infty}\frac{(\Psi'(s))^2-\Psi(s)\Psi''(s)}{(\Psi'(s))^2} \\ & =&\frac{I_{\infty}-1}{I_{\infty}}. \end{matrix}
(2.3)
-\frac{1}{\Psi'(s)}\in NRV_{I_{\infty}/(I_{\infty}-1)}.
这表明 F\in NRV_{(N+1)I_{\infty}/(I_{\infty}-1)}. q+1 (N+1)I_{\infty}/(I_{\infty}-1) q+1>N+1 q>N .
充分性. 如果 F\in NRV_{q+1}\ (q>N)
-\frac{1}{\Psi'}\in NRV_{(q+1)/(N+1)},
\lim\limits_{s\to \infty}\frac{s(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}=\frac{q+1}{N+1},\ \ -\frac{1}{\Psi'(s)}=s^{\frac{q+1}{N+1}}\hat{L}(s), \ \ \forall s\ge S_{0},
其中 S_{0} \hat{L}(s)
\begin{eqnarray*} \lim\limits_{s\to \infty}(-\frac{1}{\Psi'(s)})'\Psi(s) &=&\lim\limits_{s\to \infty}\frac{s(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}\lim\limits_{s\to \infty}\frac{-\frac{1}{\Psi'(s)}}{s}\Psi(s)\\ &=&\frac{q+1}{N+1}\lim\limits_{s\to \infty}s^{\frac{q-N}{N+1}}\hat{L}(s)\int_{s}^{+\infty}\tau^{-\frac{q+1}{N+1}}\hat{L}^{-1}(\tau){\rm d}\tau\\ &=&\frac{q+1}{N+1}\lim\limits_{s\to \infty}s^{\frac{q-N}{N+1}}\hat{L}(s)(\frac{q+1}{N+1}-1)^{-1}s^{1-\frac{q+1}{N+1}}\hat{L}^{-1}(s). \end{eqnarray*}
从而 I_{\infty}=\frac{q+1}{q-N}>1 .
从这个意义上说, F(s)=s^{q+1}\hat{L}(s), \forall s\geq S_{0}.
f(s)=s^q[(q+1)+y(s)]\hat{L}(s)\in RV_{q}, \forall s\geq S_{0},
其中 \lim\limits_{s\to \infty}y(s)=0 .
(2) 若 I_{\infty}=1
\lim\limits_{s\to \infty}\frac{s(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}=\infty.
\frac{s(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}:=y(s),\forall s>0,
\begin{equation} \label{3.7I} \frac{(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}=\frac{y(s)}{s},\forall s>0. \end{equation}
(2.4)
-\frac{1}{\Psi'(s)}=c_{0}\mbox{exp}\ \bigg(\int_{S_{0}}^{s}\frac{y(\tau)}{\tau}{\rm d}\tau\bigg),\ s>S_{0},
其中 c_{0}=-\frac{1}{\Psi'(S_{0})}.
根据 \lim\limits_{s\to \infty}y(s)=\infty, \xi>1
\begin{equation} \label{3.8I} -\frac{1}{\Psi'(\xi s)}/-\frac{1}{\Psi'(s)}=\exp \bigg(\int_{s}^{\xi s}\frac{y(\tau)}{\tau}{\rm d}\tau\bigg) =\exp \bigg(\int_{1}^{\xi}\frac{y(sv)}{v}{\rm d}v\bigg)\rightarrow\infty \ \mbox{as}\ s\rightarrow\infty. \end{equation}
(2.5)
这表明 -\frac{1}{\Psi'(s)} F
(3) 如果 F\in NRV_{N+1}
-\frac{1}{\Psi'(s)}\in NRV_{1}, -\Psi'(s)\in NRV_{-1}.
\lim\limits_{s\to \infty}\frac{s(-\frac{1}{\Psi'(s)})'}{-\frac{1}{\Psi'(s)}}=1.
\lim\limits_{s\to \infty}\frac{s\Psi'(s)}{\int_{s}^{\infty}\Psi'(\tau){\rm d}\tau}=0.
I_{\infty}=\lim\limits_{s\to \infty}\frac{\Psi''(s)\Psi(s)}{(\Psi'(s))^2}=\lim\limits_{s\to \infty}\frac{s(\frac{1}{\Psi'(s)})'}{\frac{1}{\Psi'(s)}}\frac{\int_{s}^{\infty}(-\Psi'(\tau)){\rm d}\tau}{-s\Psi'(s)}=\infty.
引理2.3 如果 f \lim\limits_{s\rightarrow 0^+}I(s)
(1) I_{0}\in (1,\infty) F\in NRVZ_{q+1}\ (q>N) . 从这个意义上说, f\in RVZ_{q}
(2) 如果 I_{0}=1 F 0
(3) 如果 F\in NRVZ_{N+1} I_{0}=\infty .
引理2.4 对于 a_{1}>0 f (0,a_{1}) \lim\limits_{s\to 0^{+}}f(s)=0 . 那么下列结论成立
(1) 如果 f 0 f\in RVZ_{q}\ (q>N)
(2) 如果 f 0 f\in RVZ_{q}\ (q<N)
证 (1) 假设 f 0 \lim\limits_{s\rightarrow 0^+}\frac{f(s)}{s^N}=0. \delta>0 f(s)<s^N, \forall 0<s<\delta.
F(s)<\frac{1}{N+1}s^{N+1}, \forall 0<s<\delta.
\int_{0}^{\delta}F(s)^{-\frac{1}{N+1}}{\rm d}s=\infty.
另外, 如果 f\in RVZ_{q}\ (q>N) F\in RVZ_{q+1}\ (q+1>N+1) . 因此, F(s)=s^{N+1}L(s) L(s) 0
\begin{eqnarray*} \int_{t}^{\infty}[(N+1)F(s)]^{-\frac{1}{N+1}}{\rm d}s &=&\int_{t}^{\infty}(N+1)^{-\frac{1}{N+1}}s^{-\frac{q+1}{N+1}}(L(s))^{-\frac{1}{N+1}}{\rm d}s\\ &=&(\frac{q-N}{N+1})^{-1}t^{\frac{N-q}{N+1}}(L(t))^{-\frac{1}{N+1}}\rightarrow\infty \ \mbox{as}\ t\rightarrow 0. \end{eqnarray*}
注2.2 如果 f\in RVZ_{N}
F(s)=s^{N+1}(\ln\frac{1}{s})^\beta, 0<s<1,
则 F\in RVZ_{N+1},\ f\in RVZ_{N}\ \mbox{且}\ \lim\limits_{s\to 0^{+}}f(s)=0.
\begin{eqnarray*} \int_{t}^{a_{1}}[(N+1)F(s)]^{-\frac{1}{N+1}}{\rm d}s &=&\int_{t}^{a_{1}}(N+1)^{-\frac{1}{N+1}}s^{-1}(\ln\frac{1}{s})^{-\frac{\beta}{N+1}}{\rm d}s\\ &=& -(N+1)^{-\frac{1}{N+1}}\frac{N+1}{N+1-\beta}(\ln\frac{1}{s})^{\frac{N+1-\beta}{N+1}}\Big|_{t}^{a_{1}}\\ &\rightarrow& \left\{\begin{array}{ll} 0,\ &\beta>N+1,\\ \infty,\ &\beta\leq N+1, \end{array} \right. \mbox{as}\ \ t\rightarrow 0^{+}. \end{eqnarray*}
引理2.5 对于 A_{1}>0 f (A_{1},\infty) \lim\limits_{s\to \infty}f(s)=\infty . 那么下列结论成立
(1) 如果 f f\in RV_{q}\ (q>N)
(2) 如果 f f\in RV_{q}\ (q<N)
注2.3 令 f\in RV_{q}\ (q=N)
例如, 对充分大的 s F(s)=s^{N+1}(\ln s)^\beta, F\in RV_{N+1},\ f\in RV_{N}\ \mbox{且}\ \lim\limits_{s\to \infty}f(s)=\infty.
\begin{eqnarray*} \int_{a_{1}}^{t}[(N+1)F(s)]^{-\frac{1}{N+1}}{\rm d}s &=&\int_{a_{1}}^{t}(N+1)^{-\frac{1}{N+1}}s^{-1}(\ln s)^{-\frac{\beta}{N+1}}{\rm d}s\\ &= &(N+1)^{-\frac{1}{N+1}}\frac{N+1}{N+1-\beta}(\ln s)^{\frac{N+1-\beta}{N+1}}\Big|_{a_{1}}^{t}\\ &\rightarrow& \left\{\begin{array}{ll} 0,\ &\beta>N+1,\\ \infty,\ &\beta\leq N+1, \end{array} \right. \mbox{as}\ \ t\rightarrow \infty. \end{eqnarray*}
由(1.17)式得 \Gamma'(s)=-[Nf(s)]^{-\frac{1}{N}},\ \Gamma''(s)=[Nf(s)]^{-\frac{1}{N}-1}f'(s),
-\frac{1}{\Gamma'(s)}=[Nf(s)]^{\frac{1}{N}}.
I_{1}(s)=\frac{f'(s)\Gamma(s)}{[Nf(s)]^{\frac{N-1}{N}}}.
假设 \lim\limits_{s\rightarrow \infty}I_1(s), \lim\limits_{s\rightarrow 0}I_1(s) I_{1\infty} I_{10}
类似于引理 2.1 -引理2.3, 还可以得到如下结果.
引理2.6 如果 f \lim\limits_{s\rightarrow \infty}I_1(s), \lim\limits_{s\rightarrow 0}I_1(s) I_{1\infty}\ge 1,\ I_{10}\geq 1.
引理2.7 如果 f \lim\limits_{s\rightarrow \infty}I_1(s)
(1) I_{1\infty}\in (1,\infty) F\in NRV_{q+1}\ (q>N) . 从这个意义上说, f\in RV_{q}
(2) 如果 I_{1\infty}=1 F
(3) 如果 F\in NRV_{N+1} I_{1\infty}=\infty .
引理2.8 如果 f \lim\limits_{s\rightarrow 0^+}I_1(s)
(1) I_{10}\in (1,\infty) F\in NRVZ_{q+1}\ (q>N) . 从这个意义上说, f\in RVZ_{q}
(2) 如果 I_{10}=1 F 0
(3) 如果 F\in NRVZ_{N+1} I_{10}=\infty .
接下来我们考虑 J(s)
J(s)=\frac{p(s)\int_{0}^s[N\tilde P(\tau)]^\frac{1}{N}{\rm d}\tau}{[N\tilde P(s)]^\frac{N+1}{N}}.
引理2.9 设 p\in {\cal P}_{finite} J_{0}\geq 0.
引理2.10 设 p\in {\cal P}_{finite} \lim\limits_{s\rightarrow 0^+}I_1(s)
(1) J_{0}\in (0,\infty) \tilde P\in NRVZ_{q+1} -1>q>-N-1 . 从这个意义上说, p\in RVZ_{q}
(2) 如果J_{0}=0 \tilde P 0
(3) 如果 \tilde P\in NRVZ_{-N} J_{0}=\infty .
引理2.11 设 p\in {\cal P}_{finite}
(1) 如果 p 0 p\in RVZ_{q} q>-N-1
(2) 如果 p 0 p\in RVZ_{q} q<-N-1
证 (1) 如果 p 0 \lim\limits_{s\rightarrow 0^+}s^2 p(s)=0. \delta>0 p(s)<s^{-2}, \ \forall \ 0<s<\delta. \tilde P(s)<s^{-1}, \ \forall \ 0<s<\delta.
\int_{0}^{s}[N\tilde P(\tau)]^{\frac{1}{N}}{\rm d}\tau<\infty.
令 p\in RVZ_{q} q>-N-1 \tilde P\in RVZ_{q+1} q+1>-N . 因此 \tilde P(s)=s^{q+1}L(s) L(s) 0
\begin{eqnarray*} \int_{0}^{t}[N\tilde P(s)]^{\frac{1}{N}}{\rm d}s&=&\int_{0}^{t}N^{\frac{1}{N}}s^{\frac{q+1}{N}}(L(s))^{\frac{1}{N}}{\rm d}s\\ &=&N^{\frac{1}{N}}(\frac{q+1}{N}+1)^{-1}t^{\frac{q+1}{N}+1}(L(t))^{\frac{1}{N}}\rightarrow 0\ \mbox{as}\ t\rightarrow 0, \end{eqnarray*}
(2) 设 p 0
\lim\limits_{s\rightarrow 0^+}p(s)s^{N+1}=\infty.
因此存在很小的 \delta>0 M>0 p(s)>Ms^{-N-1}, \ \forall \ 0<s<\delta.
\tilde P(s)>\frac{M}{N}s^{-N}, \forall \ 0<s<\delta.
\int_{0}^{s}[N\tilde P(\tau)]^{\frac{1}{N}}{\rm d}\tau=\infty.
如果 p\in RVZ_{q} q<-N-1 \tilde P\in RVZ_{q+1} q+1<-N . 从而 \tilde P(s)=s^{q+1}L(s) L(s) 0
\begin{eqnarray*} \int_{0}^{t}[N\tilde P(s)]^{\frac{1}{N}}{\rm d}s&=&\int_{0}^{t}N^{\frac{1}{N}}s^{\frac{q+1}{N}}(L(s))^{\frac{1}{N}}{\rm d}s\\ &=&N^{\frac{1}{N}}(-\frac{q+1}{N}-1)^{-1}t^{\frac{q+1}{N}+1}(L(t))^{\frac{1}{N}}\rightarrow \infty\ \mbox{as}\ t\rightarrow 0. \end{eqnarray*}
注2.4 如果 p\in RVZ_{q} q=-N-1 \tilde P(s)=s^{-N}(\ln s)^{-\beta}, \tilde P\in RVZ_{-N}, p\in RVZ_{-N-1}.
\begin{eqnarray*} \int_{0}^{t}[N\tilde P(s)]^{\frac{1}{N}}{\rm d}s &=&\int_{0}^{t}N^{\frac{1}{N}}s^{-1}(\ln s)^{-\frac{\beta}{N}}{\rm d}s\\ &= &N^{\frac{1}{N}}\frac{N}{N-\beta}(\ln s)^{\frac{N-\beta}{N}}\Big|_{0}^{t}\\ &\rightarrow& \left\{\begin{array}{ll} 0,\ &\beta>N,\\ \infty,\ &\beta\leq N, \end{array} \right. \mbox{as}\ \ t\rightarrow 0^{+}. \end{eqnarray*}
3 成对条件的比较
在本节, 我们主要分析对f \Psi,\ \Gamma,\ I_{\eta},\ I_{1\eta}
\int_{\eta^+}[F(s)]^{-1/(N+1)}{\rm d}s,\ \int_{\eta^{+}}[f(s)]^{-1/N}{\rm d}s
第一个结果是处理 \int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty \int_{s}^\infty [f(\tau)]^{-1/N}{\rm d}\tau<\infty
定理3.1 (1) 如果 f\in RV_p(p>N) f
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty \ \mbox{且}\ \int_{s}^\infty [f(\tau)]^{-1/N}{\rm d}\tau<\infty.
(2) 如果 f\in RV_p(p<N) f
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty \ \mbox{且}\ \int_{s}^\infty [f(\tau)]^{-1/N}{\rm d}\tau=\infty.
(3) 如果 f\in RV_N \int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty \int_{s}^\infty [f(\tau)]^{-1/N}{\rm d}\tau<\infty.
证 (1) 如果 f\in RV_p(p> N) F\in RV_{p+1},\ f(s)=s^pL(s),\ F(s)=s^{p+1}L(s), L(s)
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty,\int_s^\infty [f(\tau)]^{-1/N}{\rm d}\tau <\infty.
另外, 如果 f \rho>N \lim\limits_{s\rightarrow\infty}\frac{f(s)}{s^{\rho}}=\infty. M>0 S>0 s>S f(s)>Ms^{\rho} f(s)^{-\frac{1}{N}}<[Ms^{\rho}]^{-\frac{1}{N}}.
由 \tau (\tau>S) \infty
\int_\tau^\infty [f(s)]^{-1/N}{\rm d}s <\infty.
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty.
(2) 如果 f\in RV_p (p<N)
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty,\int_s^\infty [f(\tau)]^{-1/N}{\rm d}\tau =\infty.
另外, 如果 f \lim\limits_{s\rightarrow\infty}\frac{f(s)}{s^N}=0.
因此存在 m>0 S>0 s>S f(s)<ms^N
f(s)^{-\frac{1}{N}}>[ms^N]^{-\frac{1}{N}}.
从\tau (\tau>S) \infty
\int_\tau^\infty [f(s)]^{-1/N}{\rm d}s =\infty.
\int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty.
(3) 如果 f\in RV_N 12 ,引理 2.1]知
\lim_{t\to\infty} \frac{F(t)^{1/(N+1)}}{f(t)^{1/N}}=0.
\int_s^\infty [f(\tau)]^{-1/N}{\rm d}\tau<\infty.
反过来, 对充分大的 u f(u)=u^N(\log u)^\alpha,\alpha\in (N, N+1],
\int_s^\infty [f(\tau)]^{-1/N}{\rm d}\tau <\infty
且 \int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty.
这表明\int_{s}^\infty [f(\tau)]^{-1/N}{\rm d}\tau<\infty \int_{s}^\infty [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty.
下面的结果是处理 I_0\neq \infty \int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau=\infty
定理3.2 I_0\neq \infty \int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau=\infty
证 根据引理 2.12, 2.13, 我们可以从 I_0\neq \infty \int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau=\infty .
f_1(x)=\frac{\ln x+\sqrt{(\ln x)^2+4}}{2}
表示 g(x)={\rm e}^{x-\frac{1}{x}}
\lim\limits_{x\rightarrow 0^+}f_1(x)=0,\ \lim\limits_{x\rightarrow \infty}f_1(x)=\infty
且 f_1(x) (0,\infty)
f_1(x)\sim -\frac{1}{\ln x}(x\rightarrow 0^+),\ f_1(x)\sim \ln x(x\rightarrow \infty).
(3) f_1(x) 0 \infty
F(x)=x^{N+1}[f_1(x)]^{\beta}(\beta> N+1),
F(x)\sim x^{N+1}(-\frac{1}{\ln x})^{\beta}(x\rightarrow 0^+),~F(x)\sim x^{N+1}(\ln x)^{\beta}(x\rightarrow \infty).
\int_{s}^\infty [(N+1)F(\tau)]^{-1/(N+1)}{\rm d}\tau\sim\int_{s}^\infty (N+1)^{-1/(N+1)}x^{-1}(\ln x)^{-\frac{\beta}{N+1}}{\rm d}\tau<\infty,
\int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau\sim\int_{0^{+}} x^{-1}(-\ln x)^{\frac{\beta}{N+1}}{\rm d}\tau=\infty,
\begin{eqnarray*} I_0&=&\lim\limits_{s\rightarrow 0^+}\frac{f(s)\Psi(s)}{[(N+1)F(s)]^{\frac{N}{N+1}}}\\ & =&\lim\limits_{s\rightarrow 0^+}\frac{s^Nf_1^{\beta}\bigg[(N+1)+\frac{\beta}{\sqrt{(\ln s)^2+4}}\bigg](-\ln x)^{\frac{N+1+\beta}{N+1}}}{(N+1-\beta)s^Nf_1^{\frac{N\beta}{N+1}}}\\ &=&\infty. \end{eqnarray*}
这表明由 \int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau=\infty I_0\neq\infty . 定理 3.2 得证.
定理 3.3 将要处理 I_{10}\neq \infty \int_{0^+}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=\infty
定理3.3 I_{10}\neq \infty \int_{0^+}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=\infty
证 令 f_1(x)
f(x)=x^N[f_1(x)]^{\beta}(\beta> N),
f(x)\sim x^{N}(-\frac{1}{\ln x})^{\beta}(x\rightarrow 0^+),~f(x)\sim x^{N}(\ln x)^{\beta}(x\rightarrow \infty).
\int_{0^+}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=\infty,\ I_{10}=\infty.
\int_{0^+}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=\infty
不能蕴含 I_{10}\neq\infty . 定理 3.3 得证.
\int_{0^+}[F(\tau)]^{-\frac{1}{N+1}}{\rm d}\tau=\infty
\int_{0^+}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=\infty
定理3.4 (1) 如果 f\in RVZ_p,p>N f 0
\int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau=\infty\ \mbox{且}\ \int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty.
(2) 如果 f\in RVZ_p(p<N) f
\int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau<\infty\ \mbox{且}\ \int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau<\infty.
\int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau=\infty
\int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty,
证 因为(1) 和 (2) 的证明过程类似于定理 3.1 的证明, 所以省略.
f(s)=(N+1)s^NL(s)+s^{N+1}L'(s)
\int_{0^{+}}[f(\tau)]^{-1/N}{\rm d}\tau=\infty,
其中L(s)\in C^1(0,a)(a>0) f\in RVZ_N F(s)=s^{N+1}L(s).
如果\lim\limits_{s\rightarrow 0^+}L(s)=c\geq 0,
\int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau =\int_{0^+}\tau^{-1}(L(\tau))^{-1}{\rm d}\tau >k\int_{0^+}\tau^{-1}{\rm d}\tau =\infty.
如果 \lim\limits_{s\rightarrow 0^+}L(s)=\infty,
\lim\limits_{s\rightarrow 0^+}\frac{[F(s)]^{\frac{N}{N+1}}}{f(s)}=\lim\limits_{s\rightarrow 0^+}\frac{[L(s)]^{\frac{N}{N+1}}}{(N+1)L(s)+sL'(s)} =\lim\limits_{s\rightarrow 0^+}\frac{1}{(N+1)[L(s)]^{\frac{1}{N+1}}+\frac{sL'(s)}{[L(s)]^{\frac{N}{N+1}}}}.
L(s)=c_0\exp\left(\int_{A_1}^s\frac{y(\tau)}{\tau}{\rm d}\tau\right).
\lim\limits_{s\rightarrow 0^+}\frac{sL'(s)}{[L(s)]^{\frac{N}{N+1}}}=0.
\lim\limits_{s\rightarrow 0^+}\frac{[F(s)]^{\frac{N}{N+1}}}{f(s)}=0.
\int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty.
F(s)=s^{N+1}(\ln\frac{1}{s})^\beta,\ N<\beta\leq N+1.
\int_{0^+} [F(\tau)]^{-1/(N+1)}{\rm d}\tau=\infty,\ \int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau<\infty.
4 文献[31 ], [33 ]和[34 ]中边界爆破解的最优估计
在本节, 我们将对已有文献中的一些最优估计的结果作进行比较, 并阐述条件和估计之间的关系: 何种条件导致何种估计.
定理4.1 ([31 ,定理 1.2]) 假设 K(x) f(u) \eta\in \Bbb R^1
注 4.1 由定理 4.1 的证明知问题(1.1)的解 u(x)
\begin{equation}\label{4.1}\gamma_1(c_1d(x))\leq u(x)\leq \psi(c_2d(x)), x\in \Omega,\end{equation}
(4.1)
其中 0<c_2<c_1 \gamma_1(s)
\Gamma_1(s)=-\int_s^{\infty}[f(\tau)]^{-\frac{1}{N}}{\rm d}\tau=-\Gamma(s)
的逆, 不管\int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau=\infty, \int_{0^+} [f(\tau)]^{-1/N}{\rm d}\tau<\infty.
注 4.2 Zhang 和 Feng[32 ] 给出了定理 4.1 中条件(1.3)必要性的证明.
当 b(x) K(x) [34 ] 研究了问题(1.1). 假设 f b
(S_1 ) f\in C^1[0,\infty), f(0)=0, f [0,\infty)
(S_{01} ) f\in C^1(R), f(s)>0,\forall s\in R, f \Bbb R
(f_1 ) \int_{s}^{\infty}\frac{{\rm d}\tau}{H(\tau)}<\infty, H(s)=f(s)^{1/N}.
(f_{2}) E^{\infty}_{f}\in (0,\infty) \lim\limits_{s\rightarrow \infty}I_{f}(s)=E^{\infty}_{f},
I_{f}(s)=H'(s)\int_{s}^{\infty}\frac{{\rm d}\tau}{H(\tau)}.
(f_{3}) \eta>-\infty \int_{\eta^{+}}\frac{{\rm d}\tau}{H(\tau)}=\infty E^{\eta}_{f}\in (0,\infty) \lim\limits_{s\rightarrow \eta^{+}}I_{f}(s)=E^{\eta}_{f}.
(f_{4}) \eta=-\infty E^{-\infty}_{f}\in (0,\infty) \lim\limits_{s\rightarrow -\infty}I_{f}(s)=E^{-\infty}_{f}.
(B_{1}) b\in C^{\infty}(\Omega) \Omega
(b_{1}) b_{i}(i=1,2) \sigma>-1-N b_1(d(x))^{\sigma}\leq b(x)\leq b_2(d(x))^{\sigma}, x\in \Omega.
(b_{3}) \mu>1 b_{i}(i=1,2)
b_1(d(x))^{-1-N}(-\ln(d(x)))^{-N\mu}\leq b(x)\leq b_2(d(x))^{-1-N}(-\ln(d(x)))^{-N\mu}, x\in \Omega.
由第一节知在条件 (b_{1}) _{3}) P_{finite}
(B) 存在正数 b_{i}(i=1,2) p\in P_{finite} b_1p(d(x))\leq b(x)\leq b_2p(d(x)), x\in \Omega.
因此, 可以把 Zhang 在文献[34 ]中的定理描述为如下定理4.2.
定理4.2 ([34 ,定理 2.4]) 令 f _1 )( 或者 S_{01} ) , (f_1 ) , (f_2 ) 和条件 (f_3 )( 或者 (f_4 )). 如果 b _{1}) u
\begin{equation}\label{4.2}\gamma(c_1\omega(d(x)))\leq u(x)\leq \gamma(c_2\omega(d(x))),\end{equation}
(4.2)
注 4.3 如果定理 4.2 中的 b\in C^{\infty}(\bar\Omega) u
\begin{equation}\label{4.3}\gamma(c_1d(x))\leq u(x)\leq \gamma(c_2d(x)),\end{equation}
(4.3)
注 4.4 由文献[31 ,定理 4.1]知, 当 \eta=-\infty _{4})
注 4.5 由(1.18)式, 条件 (f_{2}) _{3}) E^{\eta}_{f},\ E^{\infty}_{f} I_{1\eta},\ I_{1\infty} \eta>-\infty \eta=0 . 那么 (f_{2}) I_{1\infty}\neq \infty _{3}) I_{10}\neq \infty . 由文献[34 ,定理 4.2]的证明过程可以看出, 为了使用 \gamma f I_{1\infty}\neq \infty . 由引理 2.7 知I_{1\infty}\neq \infty f\notin RV_N . 然而, 当我们使用 \psi
同时, 作者为了控制下估计, 对 f I_{10}\neq \infty . 不过, 根据定理 3.3 和定理 3.4 可知条件 I_{10}\neq \infty b\in C^{\infty}(\bar\Omega)
以下定理是来自于 Zhang 和 Feng[33 ] (当 k=N
定理4.3 ([33 ,定理 1.3]) 假设 K(x) K\in C^{\infty}(\bar\Omega) f(u) I_{0}\neq \infty . 那么问题(1.1)存在一个严格凸解 u u
\begin{equation}\label{4.4}\psi(c_{1}d(x))\leq u(x)\leq \psi(c_{2}d(x)), x\in \Omega,\end{equation}
(4.4)
定理4.4 ([33 ,定理 1.5]) 假设 K(x) {\cal P}_{finite} p(t) \partial \Omega
k_{2}p(d(x))\leq H(x)\leq k_{1}p(d(x)),
其中 k_{1}>k_{2}>0 . 另外, 假定 f(u) I_{0}\neq \infty I_{\infty}=\infty J_{0}=\infty u u
\begin{equation} \label{4.5}\psi(c_{1}[\omega(d(x))]^{\frac{N}{N+1}})\leq u(x)\leq \psi(c_{2}[\omega(d(x))]^{\frac{N}{N+1}}), x\in \Omega,\end{equation}
(4.5)
注 4.6 条件(1.3)的必要性在定理 4.4 中亦成立.
注 4.7 在定理 4.3 中, 用 I_0\neq \infty I_0\neq \infty
注 4.8 由引理 2.3 和引理 2.8 知 I_0\neq \infty I_{10}\neq \infty . 由引理 2.2 和引理 2.7 知 I_{\infty}\neq \infty I_{1\infty}\neq \infty . 在这种情况下 f\notin RV_N f\notin RVZ_N \gamma \psi
f=u^p(p>N),\ p(x)=x^{\beta}(\beta>-1-N)
时,(4.2)式就是(4.4)式. 然而, 由定理 4.4 知我们有更多的选择, 即如果 J_{0}\neq\infty I_{\infty}=\infty . 在这种情况下,(4.4)式依然成立, 不过我们得不到(4.2)式中上界估计. 故定理 4.2 中的条件比定理 4.4 中的条件强.
5 K(x)
在这一部分我们研究当K(x)
(K1) 在 \partial\Omega K(x)\geq Cd(x)^{-\gamma} \gamma\geq 2N C
如果 f(u)
证 用反证法. 假如问题(1.1)有一个严格凸解 u . 对于 x\in \Omega d(x)<d_0 d_0
v(y)=u(x+d(x)y),\ y\in B_{1/2}(0).
1/2d(x)\leq d(x+d(x)y)\leq 3/2 d(x), \forall y\in B_{1/2}(0).
\begin{eqnarray*} M[v]&=&d(x)^{2N}M[u]\\ &=&d(x)^{2N}K(x+d(x)y)f(u)\\ &\geq& Cd(x)^{2N}d(x+d(x)y)^{-\gamma}f(v)\\ &\geq& Cd(x)^{2N}(3/2d(x))^{-\gamma}f(v)\\ &\geq& Cf(v) \ \mbox{in} \ B_{1/2}(0), \end{eqnarray*}
其中 C v\leq V V 31 ,定理1.1]可得)
\left\{\begin{array}{ll} M[V]=Cf(V) \ &\mbox{在$ B_{1/2}(0)$内},\\ V= +\infty \ &\mbox{在$ \partial B_{1/2}(0)$上}. \end{array} \right.
由此可得 u(x)=v(0)\leq V(0) u \partial\Omega
注 5.1 部分证明思路来自 García-Melián[11 ] .
(K1)' 存在函数 p(t)\in RVZ_r(r\leq -2N) \Omega K(x)\geq Cp(d(x) C
定理5.2 设 K(x) f(u)
证 用反证法. 假如问题(1.1)有一个严格凸解 u . 对于 x\in \Omega d(x)<d_0 d_0
v(y)=u(x+p(d(x))^{-1/2N}y),\ y\in B_{1/2}(0).
因为 p(t)\in RVZ_r(r<-2N) p(d(x))^{-1/2N}\leq d(x) . 从而 x+p(d(x))^{-1/2N}y\in \Omega,
1/2d(x)\leq d(x+p(d(x))^{-1/2N}y)\leq 3/2 d(x), \forall y\in B_{1/2}(0).
又因为 p(t)\in RVZ_r p(3/2d(x))\geq m_0p(d(x)).
\begin{array}{ll} M[v]=p(d(x))^{-1}M[u]\\ \ \ \ \ \ \ \ =p(d(x))^{-1}K(x+p(d(x))^{-1/2N}y)f(u)\\ \ \ \ \ \ \ \ \geq Cp(d(x))^{-1}p(d(x+p(d(x))^{-1/2N}y))f(v)\\ \ \ \ \ \ \ \ \geq Cp(d(x))^{-1}p(3/2d(x))f(v)\\ \ \ \ \ \ \ \ \geq Cf(v) \ \mbox{in} \ B_{1/2}(0). \end{array}
注 5.3 由以上定理 5.1, 5.2, 我们给出以下表格. 在 (1) 和 (2) 的情况下问题(1.1)有严格凸解. 在 (3)-(7) 的情况下问题(1.1)没有严格凸解. 在 (8)-(10) 的情况下现在还无法确定是否有严格凸解.
参考文献
View Option
[2]
Bingham N H Goldie C M Teugels J L Regular Variation, Encyclopedia Math Appl. Cambridge : Cambridge University Press , 1987
[本文引用: 3]
[3]
Caffarelli L Interior W^{2,p}
Ann Math, 1990 , 131 135 -150
DOI:10.2307/1971510
URL
[4]
Caffarelli L Nirenberg L Spruck J The Dirichlet problem for nonlinear second-order elliptic equations I. Monge-Ampère equations
Comm Pure Appl Math, 1984 , 37 369 -402
DOI:10.1002/cpa.3160370306
URL
[本文引用: 1]
[5]
Cheng S Y Yau S T On the regularity of the Monge-Ampère equation {\rm det}((\partial ^2u/\partial x_{i}\partial x_{j})) = F(x, u)
Comm Pure Appl Math, 1997 , 30 41 -68
DOI:10.1002/cpa.3160300104
URL
[本文引用: 1]
[6]
Cheng S Y Yau S T On the existence of a complete Kähler metric on noncompact complex manifolds and the regularity of Fefferman's equation
Comm Pure Appl Math, 1980 , 33 507 -544
DOI:10.1002/cpa.3160330404
URL
[本文引用: 1]
[7]
Cheng S Y Yau S T The real Monge-Ampère equation and affine flat structures
//Chern S S, Wu W. Proceedings of 1980 Beijing Symposium on Differential Geometry and Differential Equations, Vol 1 . Beijing : Science Press , 1982 : 339 -370
[本文引用: 1]
[8]
Chuaqui M Cortázar C Elgueta M Flores C García-Melián J Letelier R On an elliptic problem with boundary blow-up and a singular weight: the radial case
Proc Roy Soc Edinburgh, 2003 , 133 1283 -1297
DOI:10.1017/S0308210500002936
URL
[9]
C\hat{i} rstea F C Trombetti C On the Monge-Ampère equation with boundary blow-up: existence, uniqueness and asymptotics
Calc Var Partial Differential Equations, 2008 , 31 167 -186
DOI:10.1007/s00526-007-0108-7
URL
[10]
Du Y Order Structure and Topological Methods in Nonlinear Partial Differential Equations
Singapore: World Scientific, 2006
[12]
Gladiali F Porru G Estimates for explosive solutions to p - Laplace equations, Progress in Partial Differential Equations (Pont-á-Mousson 1997)
Vol 1 . Pitman Res Notes Math Series, Longman, 1998 , 383 117 -127
[本文引用: 1]
[15]
Karamata J Sur un mode de croissance régulière. Théorèmes fondamentaux
Bull Soc Math France, 1993 , 61 55 -62
[本文引用: 1]
[17]
Lazer A C McKenna P J On singular boundary value problems for the Monge-Ampère operator
J Math Anal Appl, 1996 , 197 341 -362
DOI:10.1006/jmaa.1996.0024
URL
[本文引用: 2]
[18]
Matero J The Bieberbach-Rademacher problem for the Monge-Ampère operator
Manuscripta Math, 1996 , 91 379 -391
DOI:10.1007/BF02567962
URL
[本文引用: 2]
[20]
Mohammed A Existence and estimates of solutions to a singular Dirichlet problem for the Monge-Ampère equation
J Math Anal Appl, 2008 , 340 1226 -1234
DOI:10.1016/j.jmaa.2007.09.014
URL
[本文引用: 1]
[21]
Olofsson A Apriori estimates of Osserman-Keller type
Differ Integral Equ, 2003 , 16 737 -756
[本文引用: 1]
[23]
Pogorelov A V The Multidimensional Minkowski Problem. New York : Wiley , 1978 .
[24]
Rademacher H Einige Besondere Probleme Partieller Differentialgleichungen
in: Die Differential- und Integralgleichungen, der Mechanik und Physikl. New York : Rosenberg , 1943
[本文引用: 1]
[26]
Seneta E Regular Varying Functions, Lecture Notes in Math. Heidelberg : Springer-Verlag , 1976
[本文引用: 1]
[27]
Trudinger N Wang X Boundary regularity for the Monge-Ampère and affine maximal surface equations
Ann Math, 2008 , 167 993 -1028
DOI:10.4007/annals.2008.167.993
URL
[29]
Wan H Shi Y Liu W Refined second boundary behavior of the unique strictly convex solution to a singular Monge-Ampère equation
Adv Nonlinear Anal, 2022 , 11 321 -356
[本文引用: 1]
[30]
Yang H Chang Y On the blow-up boundary solutions of the Monge-Ampère equation with singular weights
Commun Pure Appl Anal, 2012 , 11 697 -708
[本文引用: 3]
[31]
Zhang X Du Y Sharp conditions for the existence of boundary blow-up solutions to the Monge-Ampère equation
Calc Var Partial Differential Equations, 2018 , 57 30
DOI:10.1007/s00526-018-1312-3
URL
[本文引用: 14]
[32]
Zhang X Feng M Boundary blow-up solutions to the Monge-Ampère equation: Sharp conditions and asymptotic behavior
Adv Nonlinear Anal, 2020 , 9 729 -744
[本文引用: 3]
[33]
Zhang X Feng M The existence and asymptotic behavior of boundary blow-up solutions to the k - Hessian equation
J Differential Equations, 2019 , 267 4626 -4672
DOI:10.1016/j.jde.2019.05.004
URL
[本文引用: 7]
[35]
Zhang Z Boundary behavior of large solutions to the Monge-Ampère equations with weights
J Differential Equations, 2015 , 259 2080 -2100
DOI:10.1016/j.jde.2015.03.040
URL
\Delta u={\rm e}^{u}
3
1916
... 据我们所知, 边界爆破解是由 Bieberbach[1 ] 率先进行了研究. 确切地说, Bieberbach[1 ] 研究了如下N=2
... [1 ] 研究了如下N=2
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
3
1987
... 在这一节, 我们将回顾和 Karamata 正规变化理论相关的概念和结论, 详细内容请见参考文献[2 ,15 ,26 ]. 另外, 我们还将研究 I_{0}, I_{\infty}, I_{10} I_{1\infty}
... 命题2.7 (渐近行为[2 ,定理 1.5.9b]) 如果一个函数 z\in RV_{-1} \int_{s}^{\infty}z(\tau){\rm d}\tau<\infty, s>0, \int_{s}^{\infty}z(\tau){\rm d}\tau
... 证 证明过程类似于文献[2 ,定理 1.5.9 b]中的证明, 我们在这里省略掉证明过程. ...
Interior W^{2,p}
1990
The Dirichlet problem for nonlinear second-order elliptic equations I. Monge-Ampère equations
1
1984
... 由文献[4 ,定理1.1]知, 如果 K\in C^\infty(\overline \Omega) K(x) \partial\Omega
On the regularity of the Monge-Ampère equation {\rm det}((\partial ^2u/\partial x_{i}\partial x_{j})) = F(x, u)
1
1997
... 令 d(x):={\rm dist} (x,\partial\Omega) . 在文献[5 ]中, 对于某些 \delta>0 C>0 0<K(x)<Cd(x)^{\delta-N-1}\ (x\in\Omega)
On the existence of a complete K?hler metric on noncompact complex manifolds and the regularity of Fefferman's equation
1
1980
... 特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
The real Monge-Ampère equation and affine flat structures
1
1982
... 特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
On an elliptic problem with boundary blow-up and a singular weight: the radial case
2003
On the Monge-Ampère equation with boundary blow-up: existence, uniqueness and asymptotics
2008
Order Structure and Topological Methods in Nonlinear Partial Differential Equations
2006
Boundary behavior for large solutions to elliptic equations with singular weights
1
2007
... 注 5.1 部分证明思路来自 García-Melián[11 ] . ...
Estimates for explosive solutions to p
1
1998
... (3) 如果 f\in RV_N 12 ,引理 2.1]知 ...
The Monge-Ampère equation with infinite boundary value
1
2004
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
Global smoothness for a singular Monge-Ampère equation
1
2017
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
Sur un mode de croissance régulière. Théorèmes fondamentaux
1
1993
... 在这一节, 我们将回顾和 Karamata 正规变化理论相关的概念和结论, 详细内容请见参考文献[2 ,15 ,26 ]. 另外, 我们还将研究 I_{0}, I_{\infty}, I_{10} I_{1\infty}
On solutions of \Delta u=f(u)
1
1957
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
On singular boundary value problems for the Monge-Ampère operator
2
1996
... 特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
... 其中 \psi \Psi [17 ] 和 Matero[18 ] 还得到了全局估计(1.6)式. 由下面的定理 3.2 知 I_\eta\neq \infty
The Bieberbach-Rademacher problem for the Monge-Ampère operator
2
1996
... 特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
... 其中 \psi \Psi [17 ] 和 Matero[18 ] 还得到了全局估计(1.6)式. 由下面的定理 3.2 知 I_\eta\neq \infty
On the existence of solutions to the Monge-Ampère equation with infinite boundary values
2
2007
... 特别地, 由于在几何中的应用, Cheng 等[6 -7 ] 当 f(u) u f(u)=u^p p>0 ) 时, 如果 p>N K(x) \overline\Omega [17 ] 证明了问题(1.1)有一个严格的凸解. 对于 f K 0<p\leq N K\in C^\infty(\overline \Omega) f 18 -19 ]知如果 f
... 对于一般形式的 K(x) [19 ] 指出如果 K(x)
Existence and estimates of solutions to a singular Dirichlet problem for the Monge-Ampère equation
1
2008
... 在文献[20 ] 中, 对于某些 C>0 K(x)\geq Cd(x)^{-N-1}\ (x\in\Omega) [30 ] 推广了这些结果. 当 K(x)
Apriori estimates of Osserman-Keller type
1
2003
... 显然,(1.5)式等价于 \lim\limits_{s\to \eta^+}\Psi(s)=\infty. [31 ] , 或者 p - Laplacian 方程[21 ] (在这种情况下(1.5)式变为 \int_{\eta^+}[F(s)]^{-1/p}{\rm d}s=\infty ). ...
On the inequality \Delta \geq f(u)
1
1957
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
Einige Besondere Probleme Partieller Differentialgleichungen
1
1943
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
Pointwise C^{2,\alpha}
2013
1
1976
... 在这一节, 我们将回顾和 Karamata 正规变化理论相关的概念和结论, 详细内容请见参考文献[2 ,15 ,26 ]. 另外, 我们还将研究 I_{0}, I_{\infty}, I_{10} I_{1\infty}
Boundary regularity for the Monge-Ampère and affine maximal surface equations
2008
On a real Monge-Ampère functional
1990
Refined second boundary behavior of the unique strictly convex solution to a singular Monge-Ampère equation
1
2022
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
On the blow-up boundary solutions of the Monge-Ampère equation with singular weights
3
2012
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
... 在文献[20 ] 中, 对于某些 C>0 K(x)\geq Cd(x)^{-N-1}\ (x\in\Omega) [30 ] 推广了这些结果. 当 K(x)
... 下面, 我们介绍 Zhang 和 Du[31 ] 得到的一个结果. 在这个结果中, 他们对于 K(x) [30 ] 提出的条件更具有一般性. ...
Sharp conditions for the existence of boundary blow-up solutions to the Monge-Ampère equation
14
2018
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
... 众所周知, 当 K\in C^\infty(\overline \Omega)>0 f(u)=u^p f(u)={\rm e}^u [31 ] 证明了: 如果 \eta>-\infty f(u)=u^p f(u)={\rm e}^u
... 显然,(1.5)式等价于 \lim\limits_{s\to \eta^+}\Psi(s)=\infty. [31 ] , 或者 p - Laplacian 方程[21 ] (在这种情况下(1.5)式变为 \int_{\eta^+}[F(s)]^{-1/p}{\rm d}s=\infty ). ...
... 同时, 在文献[31 ,定理 1.1]中, Zhang 和 Du[31 ] 还证明了, 如果 K\in C^\infty(\overline \Omega)>0 f
... [31 ] 还证明了, 如果 K\in C^\infty(\overline \Omega)>0 f
... 下面, 我们介绍 Zhang 和 Du[31 ] 得到的一个结果. 在这个结果中, 他们对于 K(x) [30 ] 提出的条件更具有一般性. ...
... 定理 1.1 (Zhang 和 Du[31 ,定理 1.5] ) 令 K
... 注 1.1 Zhang 和 Du[31 ] 中对函数 p(t) p(t)
... 接下来有一个自然的问题:如果 K(x) f [31 ] 仅考虑了径向对称的情况, 在 f \Omega
... 由文献[31 ,定理 4.1]的证明可知: 如果 \eta=-\infty \eta\in \Bbb R f(t+\eta) f(t) u-\eta u \eta=0 . 因此, 在本文我们仅仅考虑 \eta=0
... 定理 3.4 得证.
4 文献[<xref ref-type="bibr" rid="b31">31</xref>], [<xref ref-type="bibr" rid="b33">33</xref>]和[<xref ref-type="bibr" rid="b34">34</xref>]中边界爆破解的最优估计 在本节, 我们将对已有文献中的一些最优估计的结果作进行比较, 并阐述条件和估计之间的关系: 何种条件导致何种估计. ...
... 定理4.1 ([31 ,定理 1.2]) 假设 K(x) f(u) \eta\in \Bbb R^1
... 注 4.4 由文献[31 ,定理 4.1]知, 当 \eta=-\infty _{4})
... 其中 C v\leq V V 31 ,定理1.1]可得) ...
Boundary blow-up solutions to the Monge-Ampère equation: Sharp conditions and asymptotic behavior
3
2020
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
... 有一个严格凸解, 那么问题(1.1)有一个严格凸解的条件是 f \eta\in\Bbb R^1 32 ] 中, Zhang 和 Feng 证明了(1.3)式 (如果 \eta\in\Bbb R^1
... 注 4.2 Zhang 和 Feng[32 ] 给出了定理 4.1 中条件(1.3)必要性的证明. ...
The existence and asymptotic behavior of boundary blow-up solutions to the k
7
2019
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
... 当 K\in C^\infty(\overline \Omega)>0 \eta\in\Bbb R^1 33 ] 中, Zhang 和 Feng 研究了 k - Hessian 方程 (当 k=N I(s)
... 如果假设 f K {\cal P}_{finite} p(t) K(x)\sim p(d(x)) J_{0}\neq 0 33 ,定理 1.5] (当 k=N 0<c_{2}<c_{1} u
... 定理 3.4 得证.
4 文献[<xref ref-type="bibr" rid="b31">31</xref>], [<xref ref-type="bibr" rid="b33">33</xref>]和[<xref ref-type="bibr" rid="b34">34</xref>]中边界爆破解的最优估计 在本节, 我们将对已有文献中的一些最优估计的结果作进行比较, 并阐述条件和估计之间的关系: 何种条件导致何种估计. ...
... 以下定理是来自于 Zhang 和 Feng[33 ] (当 k=N
... 定理4.3 ([33 ,定理 1.3]) 假设 K(x) K\in C^{\infty}(\bar\Omega) f(u) I_{0}\neq \infty . 那么问题(1.1)存在一个严格凸解 u u
... 定理4.4 ([33 ,定理 1.5]) 假设 K(x) {\cal P}_{finite} p(t) \partial \Omega
Optimal global and boundary behavior of large solutions to the Monge-Ampère equation
8
2020
... 其中 K(x)\equiv 1 \Omega f(u)={\rm e}^{u} . 后来, Rademacher [24 ] 把 Bieberbach[1 ] 的工作推广到了 N=3 [16 ] 和 Osserman [22 ] 分别讨论了问题(1.2)边界爆破解的存在性, 并且他们对 f [13 -14 ,29 ⇓ ⇓ ⇓ ⇓ -34 ] . ...
... 最近, Zhang[34 ] 得到了严格凸解的最优的全局估计和边界渐近行为. 作者对 f
... 关于 f K [34 ] 获得的主要结果是: 证明了问题(1.1)存在严格凸解, 并且有下面的全局渐近性质 ...
... 定理 3.4 得证.
4 文献[<xref ref-type="bibr" rid="b31">31</xref>], [<xref ref-type="bibr" rid="b33">33</xref>]和[<xref ref-type="bibr" rid="b34">34</xref>]中边界爆破解的最优估计 在本节, 我们将对已有文献中的一些最优估计的结果作进行比较, 并阐述条件和估计之间的关系: 何种条件导致何种估计. ...
... 当 b(x) K(x) [34 ] 研究了问题(1.1). 假设 f b
... 因此, 可以把 Zhang 在文献[34 ]中的定理描述为如下定理4.2. ...
... 定理4.2 ([34 ,定理 2.4]) 令 f _1 )( 或者 S_{01} ) , (f_1 ) , (f_2 ) 和条件 (f_3 )( 或者 (f_4 )). 如果 b _{1}) u
... 注 4.5 由(1.18)式, 条件 (f_{2}) _{3}) E^{\eta}_{f},\ E^{\infty}_{f} I_{1\eta},\ I_{1\infty} \eta>-\infty \eta=0 . 那么 (f_{2}) I_{1\infty}\neq \infty _{3}) I_{10}\neq \infty . 由文献[34 ,定理 4.2]的证明过程可以看出, 为了使用 \gamma f I_{1\infty}\neq \infty . 由引理 2.7 知I_{1\infty}\neq \infty f\notin RV_N . 然而, 当我们使用 \psi
Boundary behavior of large solutions to the Monge-Ampère equations with weights
2015