数学物理学报, 2023, 43(1): 132-142

用Hirota 双线性导数变换求MNLS 方程的Rogue 波解

唐宇轩, 周国全,*

武汉大学物理科学与技术学院 武汉430072

The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation

Tang Yuxuan, Zhou Guoquan,*

School of Physics and Technology, Wuhan University, Wuhan 430072

通讯作者: *周国全, E-mail: zgq@whu.edu.cn

收稿日期: 2022-05-15   修回日期: 2022-08-5  

基金资助: 国家自然科学基金(12074295)

Received: 2022-05-15   Revised: 2022-08-5  

Fund supported: The NSFC(12074295)

摘要

修正的非线性薛定谔方程(MNLS方程)与导数非线性薛定谔方程(DNLS 方程)是两个紧密相关且完全可积的非线性偏微分方程. 该文通过Hirota双线性导数变换方法, 首先求得MNLS 方程在平面简谐波背景下的空间周期解, 即Akhmediev型呼吸子解, 再通过长波极限得其Rogue波解. 根据简单的参数归零法使之自然地约化为DNLS 方程的Rogue波解, 并借助于一个积分变换将其变换为Chen-Lee-Liu方程的Rogue波解. 文章还简要讨论了MNLS方程和DNLS 方程在非局域情形整体解的存在性问题.

关键词： Rogue wave; MNLS 方程; DNLS方程; Hirota双线性导数变换; 空间周期解; 呼吸子解

Abstract

The modified nonlinear Schrodinger (MNLS for brevity) equation and the Derivative nonlinear Schrodinger (DNLS for brevity) equation are two nonlinear differential equations that are closely correlated and fully integrable. Firstly, the spatially periodic breather solution of the MNLS equation has been obtained by method of Hirota's bilinear derivative transform, and then its rogue wave solution is also obtained by a long-wave limit of the Akhmediev-type breather, which can be naturally reduced to a rogue wave solution of the DNLS equation by a simple operation of parameters. The existence of global soliton/rogue wave solutions for the MNLS/DNLS equations is briefly discussed.

Keywords： Rogue wave; MNLS equation; DNLS equation; Hirota's bilinear derivative transform; Spatially periodic solution; Breather

PDF (519KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

唐宇轩, 周国全. 用Hirota 双线性导数变换求MNLS 方程的Rogue 波解[J]. 数学物理学报, 2023, 43(1): 132-142

Tang Yuxuan, Zhou Guoquan. The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation[J]. Acta Mathematica Scientia, 2023, 43(1): 132-142

1 绪论

最近十余年来, 在非线性可积方程与孤子理论研究领域, 学者们掀起了一波又一波研究热潮探求与研究经典的局域非线性可积方程的一类特殊孤子Rogue 波(有理分式解)与高阶孤子解[1⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-15]; 另一方面学者们又在探求非局域非线性可积系统的孤子解/流氓波解及其性质[15⇓⇓⇓⇓-20]. 本文关注和研究的问题是局域的非线性可积方程的 Rogue 波解. 所谓Rogue 波, 即恶棍波, 也称怪波(freak wave), 它是非线性可积方程的一种既局限于空间, 又局限于时间的破坏性极强的特殊孤子解, 被描述为来无影去无踪的“独行客”. 探求非线性可积方程的Rogue波解的方法通常有Darboux变换法或者更进一步的Backlund变换法, 以及Hirota双线性导数变换等几种主要方法[3⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓⇓-15]. 我们注意到文献中一般首选Darboux变换或Backlund变换方法[3⇓⇓⇓⇓⇓⇓⇓⇓-12], 而运用Hirota双线性导数变换这种直接方法[13-14] 比较少见. 本文运用Hirota双线性导数变换方法, 探求修正的非线性薛定谔方程(MNLS 方程)在简谐波背景下的Rogue 波解. MNLS方程具有如下形式

$\begin{equation} {\rm i}u_t+u_{xx}+{\rm i}(|u|^2u)_x+2\gamma|u|^2u=0. \label{eq:mnls} \end{equation}$

它是非线性薛定谔方程和导数非线性薛定谔方程耦合的可积系统的对称性约化结果, 该方程有一个三重哈密顿表达方式, 其可积性因此得到保证[21],其与DNLS 方程具有紧密而直接的联系. 当方程(1.1)中的参数$\gamma=0$, MNLS方程(1.1)自然地退化为如下DNLS 方程

$ \begin{equation} {\rm i}u'_t+u'_{xx}+{\rm i}(|u'|^2u')_x=0 \label{eq:dnls} \end{equation} $

在非线性可积或近可积方程的研究领域, MNLS与DNLS方程虽有不同但又直接相关, 并具有十分重要的物理应用背景[22⇓⇓⇓-26]. 方程(1.2)可被用来描述多种物理现象, 例如, 外磁场中的某些电介质系统或铁磁(反铁磁)介质中的弱非线性电磁波; 等离子体中的阿尔芬孤波; 单模光纤中的亚皮秒或飞秒激光脉冲. 可以发现, 通过一个类似于规范变换的积分变换可直接将方程(1.2)变换为方程(1.1), 甚至还可变换为另一形式的非线性导数薛定谔方程C-L-L方程[22,29-30]. 对MNLS和DNLS方程的研究由来已久, 并已相当完善. 迄今为止, 学者们针对其多类边值条件, 通过不同途径, 求得其多种不同的孤子解. 例如零边界条件下的亮孤子解及多孤子解[22⇓⇓⇓⇓⇓⇓⇓-30], 常数边界条件下的亮/暗孤子与呼吸子解[31⇓⇓⇓⇓-36], 高阶孤子解[3⇓⇓⇓⇓⇓-9], 简谐波背景边界下的呼吸子解[14], 乃至于本文所讨论的Rogue 波解.

由于反散射方法不易用来求解非零边界条件的Rogue波解, 尤其是对于平面波背景情形的求解相当困难, 使用该法求解Rogue波具有一定的局限性, 而Hirota 双线性导数变换方法却具有独特的优势, 可以根据需要构造合适的线性指数函数, 通过调整参数关系, 使其满足简谐背景波的特殊边值条件. 又鉴于前述学者们的工作, 本文参照Akhmediev对平面波背景下的一阶空间周期解取长波极限的方法, 尝试采用双线性导数法, 直接探求MNLS 方程的Rogue 波解, 最后通过简单的参数归零的方法, 将其直接约化为DNLS 方程的Rogue 波解, 从而避免了逆向约化所需的复杂繁琐的规范变换. 本文的解也可以借助一个规范积分变换, 转化为C-L-L方程的解.

本文剩余部分内容安排如下:第2章首先导出MNLS 方程的双线性形式; 第3 章探求MNLS方程在平面背景波下的呼吸子解, 即空间周期解; 第4 章通过长波极限的方法得到相应的Rogue 波解, 并针对两个可调参数讨论Rogue波解的性质, 通过参数取零和积分变换分别约化为DNLS 方程及CLL方程的Rogue 波解; 最后一章做了总结与展望.

2 MNLS方程的双线性导数变换形式

2.1 Hirota双线性导数算符及相关性质

双线性导数算符定义如下:令 $f(x,t)$ 与 $g(x,t)$ 是变量 $x$ 与 $t$ 的可微函数, 引进微分算子 $D_x$ 与 $D_t$ 使得对任意的非负整数 $m$ 和 $n$ 有

$ \begin{equation} D^m_tD^n_xf\bullet g=(\frac{\partial }{\partial t}- \frac{\partial }{\partial t'})^m(\frac{\partial }{\partial x}- \frac{\partial }{\partial x'})^nf(x,t)g(x',t')|_{t'=t,x'=x}. \end{equation}$

例如, 我们据此可以给出如下两个常用的双线性导数变换公式

$\begin{equation} (f/g)_x=(D_xf\bullet g)/g^2, \end{equation}$
$\begin{equation} (f/g)_{xx}=(D_x^2f\bullet g)/g^2-f(D_x^2g\bullet g)/g^3. \end{equation}$

Hirota双线性导数变换还具有一个重要性质, 设$\eta_j=\omega_jt+k_jx+\eta_j^0$, 其中$j=1, 2$, $\omega_j$和$k_j$ 均为复常数. 则有

$\begin{equation} D^m_tD^n_x{\rm e}^{\eta_1}\bullet {\rm e}^{\eta_2}=(\omega_1-\omega_2)^m(k_1-k_2)^n{\rm e}^{\eta_1+\eta_2}, \end{equation}$

进而可知, 具有相同系数的线性指数函数的双线性导数为零, 即当$\omega_1=\omega_2$ 或$k_1=k_2$ 时,

$\begin{equation} D^m_tD^n_x{\rm e}^{\eta_1}\bullet {\rm e}^{\eta_2}=0. \end{equation}$

其它一些广泛应用的变换性质与公式, 可见文献[14,30]. 一个非线性方程组可以化为如下形式

$\begin{equation} F_1(D_t,D_x,\cdots )g_1\bullet f_1+F_2(D_t,D_x,\cdots )g_2\bullet f_2=0, \end{equation}$

其中$F_1(D_t,D_x,\cdots )$, 是关于$D_t$ 和$D_x$ 的多项式.

2.2 修正的非线性薛定谔方程 (MNLS)的双线性倒数变换

MNLS方程(1.1), 在以平面简谐波为背景的边界条件下存在特殊孤子解, 即空间周期波解. 首先参考在零(非零)常数边界情形MNLS(DNLS方程)方程的孤子解的特点及其一般表达形式见文献[14,22-23]. 假设其Rogue 波解具有如下典型形式

$ \begin{equation} u=g\bar{f}/f^2, \label{eq:transform} \end{equation}$

将其代入(1.1)式, 可得

$\begin{equation} \label{eq:ut transform} u_t=(g\bar{f}/f^2)_t=f^{-4}(D_tg\bar{f}\bullet f^2)=f^{-4}(f\bar{f}D_tg\bullet f-gfD_tf\bullet \bar{f}), \end{equation}$
$\begin{matrix} u_{xx}&=&(g\bar{f}/f^2)_{xx}=f^{-6}[f^2(D^2_xg\bar{f}\bullet f^2)-(g\bar{f})(D^2_xf^2\bullet f^2)] \\ &=&f^{-6}\{f^2[f\bar{f}D^2_xg\bullet f-2(D_xg\bullet f)(D_xf\bullet \bar{f})+gfD^2_xf\bullet \bar{f}] -(g\bar{f})(2ffD^2_xf\bullet f)\}, \end{matrix}$
$\begin{equation} |u|^2u=g^2\bar{g}f/f^4, \label{eq:u^2u transform} \end{equation}$
$\begin{equation} (|u|^2u)_x=f^{-4}(2g\bar{g}D_xg\bullet f+g^2D_x\bar{g}\bullet f). \label{eq:u^2ux trasform } \end{equation}$

将(2.8)-(2.11)式代入MNLS 方程(1.1), 方程可以改写为如下双线性导数形式

$\begin{equation} f\bar{f}({\rm i}D_t+D^2_x)g\bullet f+f^{-2}\{D_xf^3\bullet[g(2D_xf\bullet \bar{f}-{\rm i}g\bar{g})]\}-gf({\rm i}D_t+D^2_x)f\bullet \bar{f}+2\gamma g^2\bar{g}f=0. \label{eq:mnls bilinear derivatives form} \end{equation}$

为了求解MNLS方程在非零边界条件下的解, 此处引入待定非零常数$\lambda$, (并且当$\lambda=0$ 时, 满足零边界条件), 可将上式化为如下的三个方程构成的双线性导数方程组:

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)g\bullet f=0, \label{eq:bilinear derivatives eqution 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)f\bullet \bar{f}=2\gamma g \bar{g}, \label{eq:bilinear derivatives eqution 2nd} \end{equation}$
$\begin{equation} D_xf\bullet \bar{f}={\rm i}g\bar{g}/2. \label{eq:bilinear derivatives eqution 3rd} \end{equation}$

为了求解方程(1.1)在平面波背景下的一阶空间周期解, 即Akhmediev 呼吸子解, 按照Hirota方法的常规处理手段, 须将两个辅助函数$f(x,t)$ 和$g(x,t)$ 展开为两个摄动小参量$\epsilon $ 的级数形式. 借鉴此法处理DNLS方程零边界孤子求解的经验[14,30], 相应于一阶空间周期解, $f$ 和$g$ 的级数展开可以截止于小量$\epsilon$ 的两阶项, 故可将辅助函数$f$ 和$g$ 设为以下形式

$ \begin{equation} f=f^{(0)}+\epsilon f^{(1)}+\epsilon^2f^{(2)}, \label{eq:f expand} \end{equation}$
$\begin{equation} g=g^{(0)}+\epsilon g^{(1)}+\epsilon^2g^{(2)}, \label{eq:g expand} \end{equation}$

将式(2.16)与(2.17)式带入到(2.13)-(2.15)式中, 比较方程两边关于$\epsilon$ 的不同次幂的系数, 可以得到关于$\epsilon$ 的零次幂到四次幂的方程组:

$\epsilon^0$相关方程组

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)g^{(0)}\bullet f^{(0)}=0, \label{eq:epsilon^0 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)f^{(0)}\bullet \overline{f^{(0)}}=2\gamma g^{(0)}\overline{g^{(0)}}, \label{eq:epsilon^0 2nd} \end{equation}$
$\begin{equation} D_xf^{(0)}\bullet \overline{f^{(0)}}=\frac{\rm i}{2}g_0\bar{g_0}. \label{eq:epsilon^0 3rd} \end{equation}$

$\epsilon^1$相关方程组

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(g^{(1)}\bullet f^{(0)}+g^{(0)}\bullet f^{(1)})=0, \label{eq:epsilon^1 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(f^{(1)}\bullet \overline{f^{(0)}}+f^{(0)}\bullet \overline{f^{(1)}})=2\gamma (g^{(1)}\overline{g^{(0)}}+g^{(0)}\overline{g^{(1)}}), \label{eq:epsilon^1 2nd} \end{equation}$
$\begin{equation} D_x(f^{(1)}\bullet \overline{f^{(0)}}+f^{(0)}\bullet \overline{f^{(1)}})=\frac{\rm i}{2}(g^{(1)}\overline{g^{(0)}}+g^{(0)}\overline{g^{(1)}}). \label{eq:epsilon^1 3rd} \end{equation}$

$\epsilon^2$相关方程组

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(g^{(2)}\bullet f^{(0)}+g^{(1)}\bullet f^{(1)}+g^{(0)}\bullet f^{(2)})=0, \label{eq:epsilon^2 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(f^{(2)}\bullet \overline{f^{(2)}}+f^{(1)}\bullet \overline{f^{(1)}}+f^{(0)}\bullet \overline{f^{(2)}})=2\gamma (g^{(2)}\overline{g^{(0)}}+g^{(1)}\overline{g^{(1)}}+g^{(0)}\overline{g^{(2)}}), \label{eq:epsilon^2 2nd} \end{equation}$
$\begin{equation} D_x(f^{(2)}\bullet \overline{f^{(2)}}+f^{(1)}\bullet \overline{f^{(1)}}+f^{(0)}\bullet \overline{f^{(2)}})=\frac{\rm i}{2}(g^{(2)}\overline{g^{(0)}}+g^{(1)}\overline{g^{(1)}}+g^{(0)}\overline{g^{(2)}}). \label{eq:epsilon^2 3rd} \end{equation}$

$\epsilon^3$相关方程组

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(g^{(2)}\bullet f^{(1)}+g^{(1)}\bullet f^{(2)})=0, \label{eq:epsilon^3 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)(f^{(2)}\bullet \overline{f^{(1)}}+f^{(1)}\bullet \overline{f^{(2)}})=2\gamma (g^{(2)}\overline{g^{(1)}}+g^{(1)}\overline{g^{(2)}}), \label{eq:epsilon^3 2nd} \end{equation}$
$\begin{equation} D_x(f^{(2)}\bullet \overline{f^{(1)}}+f^{(1)}\bullet \overline{f^{(2)}})=\frac{\rm i}{2}(g^{(2)}\overline{g^{(1)}}+g^{(1)}\overline{g^{(2)}}). \label{eq:epsilon^3 3rd} \end{equation}$

$\epsilon^4$相关方程组

$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)g^{(2)}\bullet f^{(2)}=0, \label{eq:epsilon^4 1st} \end{equation}$
$\begin{equation} ({\rm i}D_t+D^2_x-\lambda)f^{(2)}\bullet \overline{f^{(2)}}=2\gamma g^{(2)}\overline{g^{(2)}}, \label{eq:epsilon^4 2nd} \end{equation}$
$\begin{equation} D_xf^{(2)}\bullet \overline{f^{(2)}}=\frac{\rm i}{2}g^{(2)}\overline{g^{(2)}}. \label{eq:epsilon^4 3rd} \end{equation}$

3 MNLS和DNLS方程的一阶空间周期解

相应于一阶空间周期解, 我们推导出$f$ 与$g$ 两函数在截断后具有如下形式

$\begin{equation} g(x,t)=\rho {\rm e}^{{\rm i}\omega t}(1+a_1{\rm e}^{px+\Omega t+\phi_0}+a_2{\rm e}^{-px+\overline{\Omega} t+\overline{\phi_0}}+Ma_1a_2{\rm e}^{(\Omega+\overline{\Omega})t+\phi_0+\overline{\phi_0}}), \label{eq:g Spatial Periodic Solution} \end{equation}$
$\begin{equation} f(x,t)={\rm e}^{{\rm i}\beta x}(1+b_1{\rm e}^{px+\Omega t+\phi_0}+b_2{\rm e}^{-px+\overline{\Omega}t+\overline{\phi_0}}+Mb_1b_2{\rm e}^{(\Omega+\overline{\Omega})t+\phi_0+\overline{\phi_0}}). \label{eq:f Spatial Periodic Solution} \end{equation}$

其推导过程简洁介绍如下. 考虑到其平面简谐波背景边界条件, 根据变换性质, 可选择$f^{(0)}$ 和$g^{(0)}$ 为

$\begin{equation} g^{(0)}=\rho {\rm e}^{{\rm i}\omega t}, \label{eq:g0} \end{equation}$
$\begin{equation} f^{(0)}={\rm e}^{{\rm i}\beta x}. \label{eq:f0} \end{equation}$

由(2.18)-(2.20)式, 可得到如下色散关系

$\begin{matrix} && \beta= \rho^2/4, \\ && \omega=2\gamma \rho^2+3\rho^4/16,\\ && \lambda=-\omega-\beta^2=-2\gamma \rho^2-\rho^4/4, \label{eq:Dispersion relationship} \end{matrix}$

其中$\rho$为实常数. 上述色散关系, 使所求得的解在无穷远处渐进地趋于平面波背景. 将(3.3)-(3.6)式代入(2.21)式,可解出$f^{(1)}$ 和$g^{(1)}$ 分别为

$\begin{equation} g^{(1)}=g^{(0)}(a_1{\rm e}^{px+\Omega t+\phi_0}+a_2{\rm e}^{-px+\overline{\Omega}t+\overline{\phi_0}}), \label{eq:g1} \end{equation}$
$\begin{equation} f^{(1)}=f^{(0)}(b_1{\rm e}^{px+\Omega t+\phi_0}+b_2{\rm e}^{-px+\overline{\Omega}t+\overline{\phi_0}}). \label{eq:f1} \end{equation}$

将(3.6)与(3.7)式代入(2.22)式得到(3.6)与(3.7)式中$a_1,a_2,b_1,b_2$ 四个参数之间的如下约束关系

$\begin{equation} a_1=b_1\frac{2\Omega+2{\rm i}p^2-p\rho^2}{2\Omega-2{\rm i}p^2-p\rho^2}, \label{eq:g1 f1 coefficient relationship 1st a1} \end{equation}$
$\begin{equation} a_2=b_2\frac{2\Omega+2{\rm i}p^2+p\rho^2}{2\Omega-2{\rm i}p^2+p\rho^2}. \label{eq:g1 f1 coefficient relationship 1st a2} \end{equation}$

将(3.6)-(3.9)式代入(2.22)和(2.23)式给出进一步的参数约束条件

$\begin{equation} b_2=\overline{b_1}\frac{\overline{\Omega}-(\rho^2+4\gamma)p+{\rm i}p^2}{\overline{\Omega}-(\rho^2+4\gamma)p-{\rm i}p^2} \label{eq:g1 f1 coefficient relationship 2nd} \end{equation}$

和色散关系

$\begin{equation} \Omega_{\pm}=\frac{1}{2}(-p\rho^2\pm\sqrt{2}\sqrt{-(2p^4+8\gamma p^2\rho^2+p^2\rho^4)}), \label{eq:g1 f1 coefficient relationship 3rd} \end{equation}$

其中$b_1$ 和$\phi_0$ 均为任意复数, 这些参数是后文生成rogue波解的重要可调参数. 再将(3.6)-(3.11)式代入(2.27)-(2.29)式,可解出$g^{(2)}$ 和$f^{(2)}$ 为

$\begin{equation} g^{(2)}=g^{(0)}Ma_1a_2{\rm e}^{(\Omega+\overline{\Omega})t+\phi_0+\overline{\phi_0}}, \label{eq:g2} \end{equation}$
$\begin{equation} f^{(2)}=f^{(0)}Mb_1b_2{\rm e}^{(\Omega+\overline{\Omega})t+\phi_0+\overline{\phi_0}}, \label{eq:f2} \end{equation}$

其中参数$M$由下式决定

$\begin{equation} M=1+\frac{4p^4}{(\Omega+\overline{\Omega})^2}. \label{eq:g2 f2 coefficient relationship} \end{equation}$

(3.12)与(3.13)式中的$f^{(2)}$, $g^{(2)}$, 连同(3.14)式, 恰好可使$\epsilon^4$ 相关的双线性方程组(2.30)-(2.32)得以满足.

综合以上结果, 将(3.3)-(3.14)式代入(3.1)与(3.2)式, 再将$f$、$g$之表达式代入假设(2.7), $u^{}=g\overline{f}/f^2$[1], 即得到MNLS方程在平面波背景下的的一阶空间周期解$u^{}$[1].

现讨论当$t\rightarrow \infty$ 时, MNLS方程一阶空间周期解的渐进行为, 及方程所处的平面简谐波背景. 当角频率$\Omega=\Omega_+$ 时, 由于$\sqrt{-(2p^4+8\gamma p^2\rho^2+p^2\rho^4)}>0$, 在$t\rightarrow -\infty$ 时, 可以得到如下渐进关系

$\begin{equation} g\rightarrow \rho \exp({\rm i}\omega t), \end{equation}$
$\begin{equation} f\rightarrow \exp({\rm i}\beta t), \end{equation}$

代入(2.7)式可得

$\begin{equation} u\rightarrow \rho\exp({\rm i}(\omega t-3\beta x)), \label{eq:t -infty} \end{equation}$

而在$t\rightarrow +\infty$

$\begin{equation} u\rightarrow \rho\exp({\rm i}(\omega t-3\beta x+\phi)). \label{eq:t +infty} \end{equation}$

(3.18)式中$\phi $ 相应于当$t$ 从负无穷至正无穷时波的相移

$\begin{equation} \exp({\rm i}\phi )=a_1 a_2 \overline{b_1} \overline{b_2}/(b_1 b_2)^2, \label{eq:phi relationship} \end{equation}$

由(3.8)-(3.10)式, 可得$|a_1 a_2 \overline{b_1} \overline{b_2}|=|b_1 b_2|$, 所以(3.19)式是个纯粹的常数相因子. 同理, 当$\Omega=\Omega_-$ 时, $u$ 的渐进行为与(3.17)、(3.18)式正好相反, 此时

$\begin{equation} \lim_{t \to + \infty} u\rightarrow \rho\exp({\rm i}(\omega t-3\beta x)), \end{equation}$
$\begin{equation} \lim_{t \to - \infty} u\rightarrow \rho\exp({\rm i}(\omega t-3\beta x+\phi)). \end{equation}$

由以上讨论可知, 方程的空间周期解的远场背景确为平面简谐波.

我们再对该周期解进行若干分析. 当相关参数取定一组特殊值, $\rho =1,{{\phi }_{0}}=0,{{b}_{1}}={\rm i},$$\gamma =1/3,\Omega ={{\Omega }_{+}}$ 时, 绘制出解的时空演化过程, 图1 给出了该解的三维图. 从中可以发现该解符合呼吸子解的特征. 当给定峰值附近所对应的时刻$t$时, 可以发现空间周期解的模在$x$方向呈现出驻波特征; 当给定空间周期解峰值相应的空间坐标时, 改变时间变量$t$, 我们发现空间周期解具有呼吸子解的特点.

图1

新窗口打开| 下载原图ZIP| 生成PPT

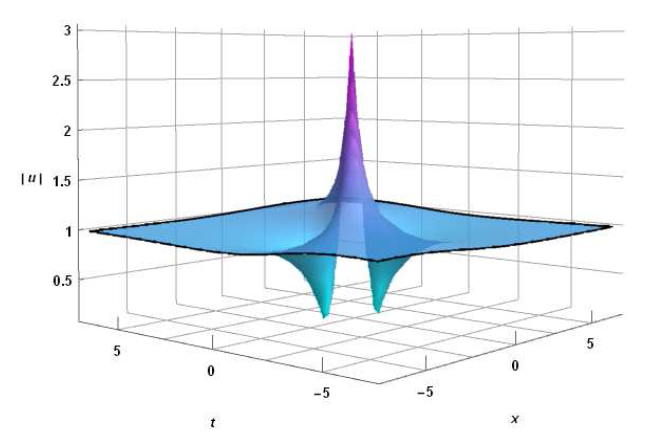
图1   MNLS方程一阶呼吸子解三维图, 参数取定为$\rho =1,{{\phi }_{0}}=0,{{b}_{1}}={\rm i}, \gamma =1/3,\Omega ={{\Omega }_{+}}$


在参数$\gamma=0$ 时, 可从MNLS方程的一阶呼吸子解出发, 自然而直接地约化而得到DNLS 方程的一阶空间周期解, 与文献[14]所得关于DNLS 方程的相应结果完全一致. 此处从略.

4 MNLS方程的Rogue波解与若干讨论

根据上一章给出的在平面波背景下的MNLS方程的一阶周期解, 下面采用长波极限的方法来构造方程相应的Rogue 波解. 在方程中系数$p$ 表示的是波矢, 应为一个纯虚数, 可令$p=qi$, 其中$q$ 是一个实数, 在$q\rightarrow 0$ 的情形下, 可以将$u^{[1]}$ 的角频率$\Omega$ 按$q$ 作级数展开

$\begin{equation} \Omega_{\pm}=\frac{q\rho^2}{2}(\sqrt{2}\sqrt{1+8\gamma/\rho^2}-{\rm i})+O(q^3), \label{eq:Omega} \end{equation}$

将$\Omega$ 保留到$q$ 的二阶项, 并引入辅助参变量函数$\sigma(\gamma,\rho)$ 以化简角频率$\Omega$ 的函数形式

$\begin{equation} \Omega=q\rho^2(\sigma-{\rm i})/2, \label{eq:Omega sigma} \end{equation}$
$\begin{equation} \sigma(\gamma,\rho)=\pm \sqrt{2}\sqrt{1+8\gamma/\rho^2}. \label{eq:sigma} \end{equation}$

再将(4.2)式代入(3.1)与(3.2)式, 再将此时的解$g$ 和$f$ 对$q$ 做级数展开. 为了得到Rogue波解, 需要确保$f$ 和$g$ 按$q$ 所作的展开式中$q^0$ 与$q^1$ 前面的系数为零, 为达成目的, 需使(3.1)与(3.2)式中的参数$b_1$,$\phi_0$ 满足如下关系

$\begin{equation} b_1=-\exp(-\phi^0), \label{eq:rouge wave condition} \end{equation}$

如此方能确保空间周期解$u^{[1]}$ 的长波极限得以存在.(4.4)式使得$f$ 和$g$ 的展开式为

$\begin{equation} f={\rm e}^{{\rm i}\beta x}Fq^2+O(q^3), \label{eq:f rouge wave solution} \end{equation}$
$\begin{equation} g=\rho {\rm e}^{{\rm i}\omega t}Gq^2+O(q^3). \label{eq:g rouge wave solution} \end{equation}$

将(4.5)与(4.6)式代入(2.7)式, 取长波极限, 可以得到Rogue 波解

$\begin{equation} {{u}_{{\rm RW}}}=\lim_{q \to 0} g \overline{f}/f^2 =\rho {\rm e}^{{\rm i}(-3\beta x+\omega t)}G\cdot \overline{F}/F^2, \label{eq:uRW mnls} \end{equation}$

其中

$\begin{matrix} \label{eq:f uRW} F&=&\frac{1}{4{{\rho }^{4}}{{\sigma }^{2}}\left( 8\gamma +{\rm i}{{\rho }^{2}}\sigma +{{\rho }^{2}} \right)}{{\rm e}^{{\rm i}\beta x}}(128\gamma +16{\rm i}{{\rho }^{2}}\sigma +16{{\rho }^{2}}+8\gamma {{\rho }^{8}}{{\sigma }^{4}}{{t}^{2}} \\ &&8\gamma {{\rho }^{8}}{{\sigma }^{2}}{{t}^{2}}+{\rm i}{{\rho }^{10}}{{\sigma }^{5}}{{t}^{2}}+{{\rho }^{10}}{{\sigma }^{4}}{{t}^{2}}+ {\rm i}{{\rho }^{10}}{{\sigma }^{3}}{{t}^{2}}+{{\rho }^{10}}{{\sigma }^{2}}{{t}^{2}}+8{{\rho }^{6}}{{\sigma }^{3}}t \\ && - 8{\rm i}{{\rho }^{6}}{{\sigma }^{2}}t-32\gamma {{\rho }^{6}}{{\sigma }^{2}}tx- 4{\rm i}{{\rho }^{8}}{{\sigma }^{3}}tx-4{{\rho }^{8}}{{\sigma }^{2}}tx+32\gamma {{\rho }^{4}}{{\sigma }^{2}}{{x}^{2}} \\ &&+ 4{\rm i}{{\rho }^{6}}{{\sigma }^{3}}{{x}^{2}}+4{{\rho }^{6}}{{\sigma }^{2}}{{x}^{2}}+16{\rm i}{{\rho }^{4}}{{\sigma }^{2}}x), \end{matrix}$
$\begin{matrix} \label{eq:g uRW} G&=&\frac{1}{4{{\rho }^{4}}{{\sigma }^{2}}\left( \sigma -2{\rm i} \right)\left( \sigma +2{\rm i} \right)\left( -8{\rm i}\gamma +{{\rho }^{2}}\sigma -{\rm i}{{\rho }^{2}} \right)}(384{\rm i}\gamma {{\sigma }^{2}}-512{\rm i}\gamma \\ & &- 112{{\rho }^{2}}{{\sigma }^{3}}-80{\rm i}{{\rho }^{2}}{{\sigma }^{2}}+64{{\rho }^{2}}\sigma -64{\rm i}{{\rho }^{2}}-8{\rm i}\gamma {{\rho }^{8}}{{\sigma }^{6}}{{t}^{2}}-40{\rm i}\gamma {{\rho }^{8}}{{\sigma }^{4}}{{t}^{2}} \\ & & -32{\rm i}\gamma {{\rho }^{8}}{{\sigma }^{2}}{{t}^{2}}+{{\rho }^{10}}{{\sigma }^{7}}{{t}^{2}}-{\rm i}{{\rho }^{10}}{{\sigma }^{6}}{{t}^{2}}+5{{\rho }^{10}}{{\sigma }^{5}}{{t}^{2}}-5{\rm i}{{\rho }^{10}}{{\sigma }^{4}}{{t}^{2}} \\ & &+ 4{{\rho }^{10}}{{\sigma }^{3}}{{t}^{2}}-4{\rm i}{{\rho }^{10}}{{\sigma }^{2}}{{t}^{2}}-128\gamma {{\rho }^{4}}{{\sigma }^{4}}t+256\gamma {{\rho }^{4}}{{\sigma }^{2}}t-24{\rm i}{{\rho }^{6}}{{\sigma }^{5}}t \\ & & -24{{\rho }^{6}}{{\sigma }^{4}}t+32{\rm i}\gamma {{\rho }^{6}}{{\sigma }^{4}}tx+128{\rm i}\gamma {{\rho }^{6}}{{\sigma }^{2}}tx-4{{\rho }^{8}}{{\sigma }^{5}}tx+4{\rm i}{{\rho }^{8}}{{\sigma }^{4}}tx \\ & & -16{{\rho }^{8}}{{\sigma }^{3}}tx+16{\rm i}{{\rho }^{8}}{{\sigma }^{2}}tx-32{\rm i}\gamma {{\rho }^{4}}{{\sigma }^{4}}{{x}^{2}}-128{\rm i}\gamma {{\rho }^{4}}{{\sigma }^{2}}{{x}^{2}}+4{{\rho }^{6}}{{\sigma }^{5}}{{x}^{2}} \\ & & -4{\rm i}{{\rho }^{6}}{{\sigma }^{4}}{{x}^{2}}+16{{\rho }^{6}}{{\sigma }^{3}}{{x}^{2}}-16{\rm i}{{\rho }^{6}}{{\sigma }^{2}}{{x}^{2}}-512\gamma {{\rho }^{2}}{{\sigma }^{2}}x+16{{\rho }^{4}}{{\sigma }^{4}}x-64{\rm i}{{\rho }^{4}}{{\sigma }^{3}}x), \end{matrix}$

式中的指数项的$\omega$ 和$\beta$ 由色散关系(3.6)式确定, 这样即得到了MNLS方程的Rogue波解. 给定参数$\gamma$,$\rho$ 并选择合适的$\sigma$ 即可唯一确定Rogue波解.

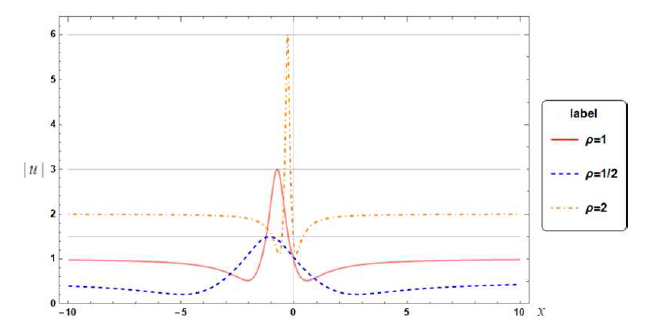
在(4.7)式中取定参数$\rho=1,\gamma=1/8,\Omega=\Omega_+$, 可得MNLS的一阶Rogue波解随时空演化的三维图形, 如图2 所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   MNLS方程一阶Rogue波解三维图, 参数取定为$\rho =1,\gamma =1/8,\Omega ={{\Omega }_{+}}$


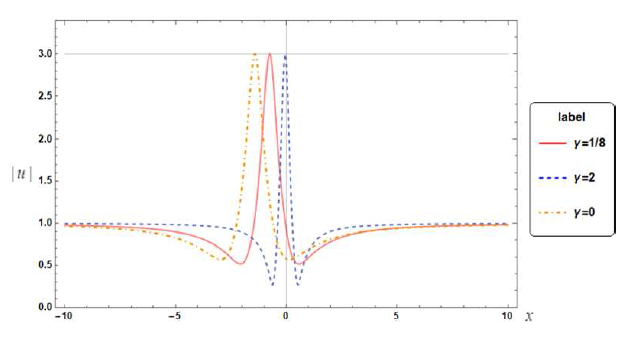
考察此Rogue波解的具体形式, 研究发现, 平面波振幅参数$\rho $决定Rogue 波解的模的极大值, 也就是波峰的大小. 给定实参数$\gamma $, 改变参数$\rho $, Rogue 波的模的峰值与平面波的振幅$\rho $似乎有确定的正比放大关系. 由此也可以看出Rogue波的生成及其峰值与边值条件密切相关, 如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   $\gamma =1/8$时, 分别取 $\rho =1,\,1/2,\,2$, 绘制其产生最大峰值时刻$|u|-x$图


另一方面实参数影响Rogue波解中波峰在时空坐标下的位置. 给定实参数$\rho $, 改变参数$\gamma $, Rogue波解的模具有不变的极大值, 但波峰的时空位置及波形均有改变. 如图4所示, 可以得到当$\gamma $ 不断增大时, Rogue波的峰值将逐渐靠近$x=0,t=0$ 的时空位置；并且随着$\gamma $ 值的增大, Rogue波的波形也愈发陡峭, 虽然具有相同的波峰值, 但波谷值确在逐渐减小. 可以预测当$\rho $保持恒定且$\gamma \to \infty $时, Rogue 波的峰值的时空位置$x\to 0,t\to 0$, 波谷将趋于零, 波峰值不发生改变.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   $\rho =1$时, 分别取 $\gamma =1/8,\,2,\,0$, 绘制其最大峰值$|u|=3$时的$|u|-x$ 图


特别当$\gamma =0$时, 此时$\beta ={{{\rho }^{2}}}/{4}$, $\omega ={3{{\rho }^{4}}}/{16}$, 方程(1.1)退化为DNLS方程(1.2), 其相应Rogue波解${{{u}'}_{{\rm RW}}}$为

$\begin{equation} {{{u}'}_{{\rm RW}}}=\lim_{q \to 0} g \overline{f}/f^2 =\rho {\rm e}^{{\rm i}(-3\beta x+\omega t)}G'\cdot \overline{F'}/F'^2, \label{eq:uRW dnls} \end{equation}$

其中$G'$,$F'$分别为

$\begin{matrix} \label{eq:f uRW dnls} F'&=&\frac{1}{4{{\rho }^{4}}{{\sigma }^{2}}(\sigma -{\rm i})}(16\sigma +{{\rho }^{8}} {{\sigma }^{5}}{{t}^{2}}-{\rm i}{{\rho }^{8}}{{\sigma }^{4}}{{t}^{2}}+ {{\rho }^{8}}{{\sigma }^{3}}{{t}^{2}}-{\rm i}{{\rho }^{8}}{{\sigma }^{2}}{{t}^{2}}-8{\rm i}{{\rho }^{4}}{{\sigma }^{3}}t \\ &&- 8{{\rho }^{4}}{{\sigma }^{2}}t-4{{\rho }^{6}}{{\sigma }^{3}}tx+4{\rm i}{{\rho }^{6}} {{\sigma }^{2}}tx+4{{\rho }^{4}}{{\sigma }^{3}}{{x}^{2}}-4{\rm i}{{\rho }^{4}}{{\sigma }^{2}}{{x}^{2}} +16{{\rho }^{2}}{{\sigma }^{2}}x-16{\rm i}), \end{matrix}$
$\begin{matrix} \label{eq:g uRW dnls} G'&=&\frac{1}{4{{\rho }^{4}}{{\sigma }^{2}}(\sigma -{\rm i})(\sigma -2{\rm i})(\sigma +2{\rm i})} (-112{{\sigma }^{3}}-80{\rm i}{{\sigma }^{2}}+64\sigma +{{\rho }^{8}}{{\sigma }^{7}}{{t}^{2}} \\ & &-{\rm i}{{\rho }^{8}}{{\sigma }^{6}}{{t}^{2}}+5{{\rho }^{8}}{{\sigma }^{5}}{{t}^{2}} -5{\rm i}{{\rho }^{8}}{{\sigma }^{4}}{{t}^{2}}+4{{\rho }^{8}}{{\sigma }^{3}}{{t}^{2}} -4{\rm i}{{\rho }^{8}}{{\sigma }^{2}}{{t}^{2}}-24{\rm i}{{\rho }^{4}}{{\sigma }^{5}}t \\ &&- 24{{\rho }^{4}}{{\sigma }^{4}}t-4{{\rho }^{6}}{{\sigma }^{5}}tx +4{\rm i}{{\rho }^{6}}{{\sigma }^{4}}tx-16{{\rho }^{6}}{{\sigma }^{3}}tx+16{\rm i}{{\rho }^{6}}{{\sigma }^{2}}tx +4{{\rho }^{4}}{{\sigma }^{5}}{{x}^{2}} \\ && -4{\rm i}{{\rho }^{4}}{{\sigma }^{4}}{{x}^{2}}+16{{\rho }^{4}}{{\sigma }^{3}}{{x}^{2}} -16{\rm i}{{\rho }^{4}}{{\sigma }^{2}}{{x}^{2}}+16{{\rho }^{2}}{{\sigma }^{4}}x -64{\rm i}{{\rho }^{2}}{{\sigma }^{3}}x-64{\rm i}). \end{matrix}$

所得结果与文献[15]的结果相符, 可以看出MNLS 方程的解将DNLS方程的解蕴含于其中. 此外, 我们还可顺便提及另一类可积的导数非线性薛定谔方程, Chen-Lee-Liu(C-L-L)方程的Rogue解, 方程如下

$\begin{equation} iv_t+v_xx+{\rm i}|v|^2v_x=0. \label{eq:CLL} \end{equation}$

它是1979年由 Chen, Lee和 Liu三人在研究一类非线性演化方程的可积性时提出的. 它的Rogue解可通过如下积分变换从DNLS 方程的Rogue解转化而来

$\begin{equation} {v}_{{\rm RW}}(x,t)={{u}'}_{{\rm RW}}\exp(\frac{\rm i}{2}\int|{{u}'}_{{\rm RW}}|^2 \,{\rm d}x ), \label{eq:CLL transform} \end{equation}$

可以发现原来的DNLS的平面波背景, 在此积分变换下仍然是一个平面波背景, 只是波矢有一定的常数变化, 不再赘述.

5 总结与前瞻

本文采用Hirota双线性导数变换方法, 得到了MNLS方程的一阶空间周期解${{u}^{}}$[1], 再通过取长波极限的方法, 将一阶周期解${{u}^{}}$[1]转化为其Rogue波解${{u}_{{\rm RW}}}$. 在求解过程中, 探求到使双线性导数变换的诸摄动方程得以成立的色散条件与参数关系, 进而探求出在长波极限下生成MNLS 方程的Rogue 波的一般条件, 最后在参数$\gamma,\rho $取不同值时, 对Rogue波的时空演化特性进行了具体讨论, 验证了空间周期解以及Rogue波解的渐进行为确实具有平面简谐波背景. MNLS方程的Rogue波解在简单的参数归零条件下, 退化为DNLS 方程的Rogue 波解, 发现其与已有文献有关DNLS方程的Rogue 波解相符合. 本文的经验表明, 似乎也可以同样采用Hirota方法和呼吸子解取长波极限的手段, 探求MNLS/DNLS 方程在平面波背景下的二阶甚至高阶周期解及其Rogue 波解, 或者在常数边界条件下, 探讨其有无有理数解, 当然在数学操作上可能需要更多的技巧与大胆的尝试. 另一方面, 在非线性方程研究领域, 还有一类问题激起了学者们的研究兴趣, 对于一些非局域的非线性方程的整体孤子解和Rogue 波解, 能否以及如何从局域的经典情形的孤子解推广而来, 许多学者已经做了一些开拓的工作和有益的尝试, 具体见文献[15⇓⇓⇓⇓-20]. 借鉴一些学者有关于此的研究成果与结论[37-38], 我们认为非局域的MNLS/DNLS 方程似乎也应该存在整体孤子解与Rogue 波解, 也应该尝试用Hirota双线性导数方法来求解, 当然我们还没有发现这方面的相关工作. 这将是一个有待继续研究的开放的问题.

参考文献

Akhmediev N, Ankiewicz A, Taki M.

Waves that appear from nowhere and disappear without a trace

Physics Letters A, 2009, 373(6): 675-678

DOI:10.1016/j.physleta.2008.12.036      URL     [本文引用: 7]

Akhmediev N, Soto-Crespo J M, Ankiewicz A.

Extreme waves that appear from nowhere: on the nature of rogue waves

Physics Letters A, 2009, 373(25): 2137-2145

DOI:10.1016/j.physleta.2009.04.023      URL     [本文引用: 1]

Wen X Y, Yang Y, Yan Z.

Generalized perturbation $(n, M)$-fold Darboux transformations and multi-rogue-wave structures for the modified self-steepening nonlinear Schrödinger equation

Physical Review E, 2015, 92(1): 012917

DOI:10.1103/PhysRevE.92.012917      URL     [本文引用: 4]

Pan C, Bu L, Chen S, et al.

General rogue wave solutions under SU (2) transformation in the vector Chen-Lee-Liu nonlinear Schrödinger equation

Physica D: Nonlinear Phenomena, 2022, 434: 133204

DOI:10.1016/j.physd.2022.133204      URL     [本文引用: 4]

He J, Xu S, Cheng Y.

The rational solutions of the mixed nonlinear Schrödinger equation

AIP Advances, 2015, 5(1): 017105

DOI:10.1063/1.4905701      URL     [本文引用: 4]

Zhao L C, Guo B, Ling L.

High-order rogue wave solutions for the coupled nonlinear Schrödinger equations-II

Journal of Mathematical Physics, 2016, 57(4): 043508

DOI:10.1063/1.4947113      URL     [本文引用: 4]

Ankiewicz A, Akhmediev N.

Rogue wave solutions for the infinite integrable nonlinear Schrödinger equation hierarchy

Physical Review E, 2017, 96(1): 012219

DOI:10.1103/PhysRevE.96.012219      URL     [本文引用: 4]

Xu S, He J, Wang L.

The Darboux transformation of the derivative nonlinear Schrödinger equation

Journal of Physics A: Mathematical and Theoretical, 2011, 44(30): 305203

DOI:10.1088/1751-8113/44/30/305203      URL     [本文引用: 4]

Guo B, Ling L, Liu Q P.

High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations

Studies in Applied Mathematics, 2013, 130(4): 317-344

DOI:10.1111/j.1467-9590.2012.00568.x      URL     [本文引用: 4]

Zhang Y, Guo L, Xu S, et al.

The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation

Communications in Nonlinear Science and Numerical Simulation, 2014, 19(6): 1706-1722

DOI:10.1016/j.cnsns.2013.10.005      URL     [本文引用: 3]

Wang L H, Porsezian K, He J S.

Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation

Physical Review E, 2013, 87(5): 053202

DOI:10.1103/PhysRevE.87.053202      URL     [本文引用: 3]

Lou S, Lin J.

Rogue waves in nonintegrable KdV-type systems

Chinese Physics Letters, 2018, 35(5): 050202

DOI:10.1088/0256-307X/35/5/050202      URL     [本文引用: 3]

Wu H, Fei J, Ma W.

Lump and rational solutions for weakly coupled generalized Kadomtsev-Petviashvili equation

Modern Physics Letters B, 2021, 35(26): 2150449

DOI:10.1142/S0217984921504492      URL     [本文引用: 3]

Zhou G, Li X.

Space periodic solutions and rogue wave solution of the derivative nonlinear Schrödinger equation

Wuhan University Journal of Natural Sciences, 2017, 22(5): 373-379

DOI:10.1007/s11859-017-1261-2      URL     [本文引用: 8]

Ma W X.

Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems

Partial Differential Equations in Applied Mathematics, 2021, 4: 100190

DOI:10.1016/j.padiff.2021.100190      URL     [本文引用: 5]

Ablowitz M J, Musslimani Z H.

Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation

Nonlinearity, 2016, 29(3): 915

DOI:10.1088/0951-7715/29/3/915      URL     [本文引用: 2]

Yang B, Yang J.

Rogue waves in the nonlocal ${\mathcal {PT}} $ PT-symmetric nonlinear Schrödinger equation

Letters in Mathematical Physics, 2019, 109(4): 945-973

DOI:10.1007/s11005-018-1133-5      [本文引用: 2]

Rogue waves in the nonlocal PT-symmetric nonlinear Schrodinger (NLS) equation are studied by Darboux transformation. Three types of rogue waves are derived, and their explicit expressions in terms of Schur polynomials are presented. These rogue waves show a much wider variety than those in the local NLS equation. For instance, the polynomial degrees of their denominators can be not only n(n+1), but also n(n-1)+1 and n2, where n is an arbitrary positive integer. Dynamics of these rogue waves is also examined. It is shown that these rogue waves can be bounded for all space and time or develop collapsing singularities, depending on their types as well as values of their free parameters. In addition, the solution dynamics exhibits rich patterns, most of which have no counterparts in the local NLS equation.

Lin J, Jin X W, Gao X L, et al.

Solitons on a periodic wave background of the modified KdV-Sine-Gordon equation

Communications in Theoretical Physics, 2018, 70(2): 119-126

DOI:10.1088/0253-6102/70/2/119      URL     [本文引用: 2]

Li L, Duan C, Yu F.

An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation

Physics Letters A, 2019, 383(14): 1578-1582

DOI:10.1016/j.physleta.2019.02.031      [本文引用: 2]

The Hirota bilinear method has been studied in a lot of local equations, but there are few of works to solve nonlocal equations by Hirota bilinear method. In this letter, we show that the nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation admits multiple complex soliton solutions. A variety of exact solutions including the single bright soliton solutions and two bright soliton solutions are derived via constructing an improved Hirota bilinear method for nonlocal complex MKdV equation. From the gauge equivalence, we can see the difference between the solution of nonlocal integrable complex MKdV equation and the solution of local complex MKdV equation. (C) 2019 Elsevier B.V.

Zhong W P, Yang Z, Beli${\rm\acute{c}}$ M, et al.

Breather solutions of the nonlocal nonlinear self-focusing Schrödinger equation

Physics Letters A, 2021, 395: 127228

DOI:10.1016/j.physleta.2021.127228      URL     [本文引用: 2]

Ma W X, Zhou R.

A coupled AKNS-Kaup-Newell soliton hierarchy

Journal of Mathematical Physics, 1999, 40(9): 4419-4428

DOI:10.1063/1.532976      URL     [本文引用: 1]

Chen Z Y, Huang N N.

Explicit N-soliton solution of the modified nonlinear Schrödinger equation

Physical Review A, 1990, 41(7): 4066-4069

DOI:10.1103/PhysRevA.41.4066      URL     [本文引用: 4]

Huang N N, Chen Z Y.

Alfven solitons

Journal of Physics A: Mathematical and General, 1990, 23(4): 439-453

DOI:10.1088/0305-4470/23/4/014      URL     [本文引用: 3]

Chen H H, Lee Y C, Liu C S.

Integrability of nonlinear Hamiltonian systems by inverse scattering method

Physica Scripta, 1979, 20(3/4): 490-492

DOI:10.1088/0031-8949/20/3-4/026      URL     [本文引用: 2]

Kaup D J, Newell A C.

An exact solution for a derivative nonlinear Schrödinger equation

Journal of Mathematical Physics, 1978, 19(4): 798-801

DOI:10.1063/1.523737      URL     [本文引用: 2]

Kawata T, Inoue H.

Exact solution of derivative nonlinear Schrödinger equation under nonvanishing conditions

J Phys Soc Jpn, 1978, 44(6): 1968-1976

DOI:10.1143/JPSJ.44.1968      URL     [本文引用: 2]

Steudel H.

The hierarchy of multi-soliton solutions of derivative nonlinear Schrödinger equation

J Phys A, 2003, 36: 1931-1946

DOI:10.1088/0305-4470/36/7/309      URL     [本文引用: 1]

Zhou G Q, Huang N N.

An $N$-soliton solution to the DNLS equation based on revised inverse scattering transform

Journal of Physics A: Mathematical and Theoretical, 2007, 40(45): 13607-13623

DOI:10.1088/1751-8113/40/45/008      URL     [本文引用: 1]

Zhou G.

A multi-soliton solution of the DNLS equation based on pure Marchenko formalism

Wuhan University Journal of Natural Sciences, 2010, 15(1): 36-42

DOI:10.1007/s11859-010-0108-x      URL     [本文引用: 2]

Zhou G, Bi X.

Soliton solution of the DNLS equation based on Hirota's bilinear derivative transform

Wuhan University Journal of Natural Sciences, 2009, 14(6): 505-510

DOI:10.1007/s11859-009-0609-7      URL     [本文引用: 4]

蔡浩.

关于MNLS方程和DNLS方程的研究

武汉大学, 2005

[本文引用: 1]

Cai H.

Research about MNLS Equation and DNLS Equation

Wuhan Univ, 2005

[本文引用: 1]

Chen X J, Lam W K.

Inverse scattering transform for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions

Physical Review E, 2004, 69(6): 066604

DOI:10.1103/PhysRevE.69.066604      URL     [本文引用: 1]

Chen X J, Yang J K, Lam W K.

$N$-soliton solution for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions

Journal of Physics A: Math Gen, 2006, 39(13): 3263-3274

DOI:10.1088/0305-4470/39/13/006      URL     [本文引用: 1]

Lashkin V M.

$N$-soliton solutions and perturbation theory for DNLS with nonvanishing condition

J Phys A, 2007, 40: 6119-6132

DOI:10.1088/1751-8113/40/23/008      URL     [本文引用: 1]

Zhou G.

A newly revised inverse scattering transform for DNLS+ equation under nonvanishing boundary condition

Wuhan University Journal of Natural Sciences, 2012, 17(2): 144-150

DOI:10.1007/s11859-012-0819-2      URL     [本文引用: 1]

Zhou G.

Explicit breather-type and pure N-Soliton solution of DNLS+ equation with nonvanishing boundary condition

Wuhan University Journal of Natural Sciences, 2013, 18(2): 147-155

DOI:10.1007/s11859-013-0907-y      URL     [本文引用: 1]

Osman M S, Almusawa H, Tariq K U, et al.

On global behavior for complex soliton solutions of the perturbed nonlinear Schrödinger equation in nonlinear optical fibers

Journal of Ocean Engineering and Science, 2022, 7(5): 431-443

DOI:10.1016/j.joes.2021.09.018      URL     [本文引用: 1]

Bourgain J.

Global Solutions of Nonlinear Schrödinger Equations

Providence, RI: American Mathematical Society, 1999

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发