用Hirota 双线性导数变换求MNLS 方程的Rogue 波解

摘要/Abstract

摘要：

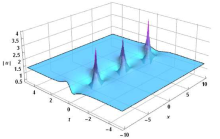
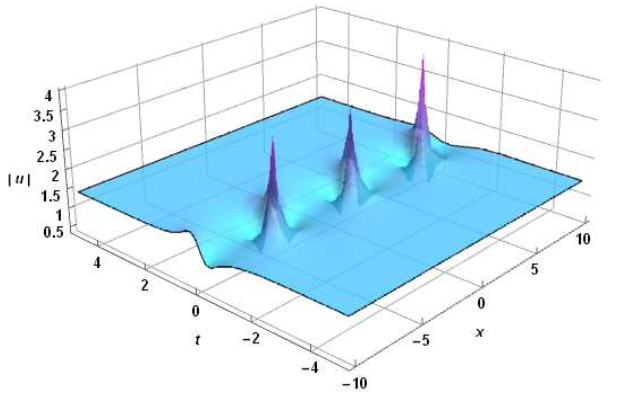
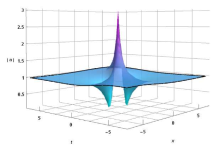
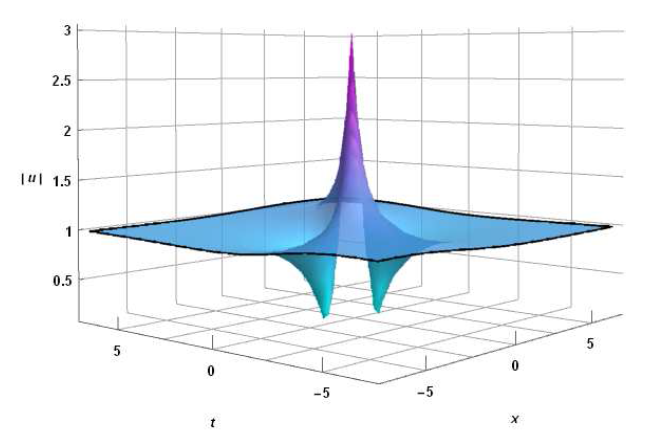
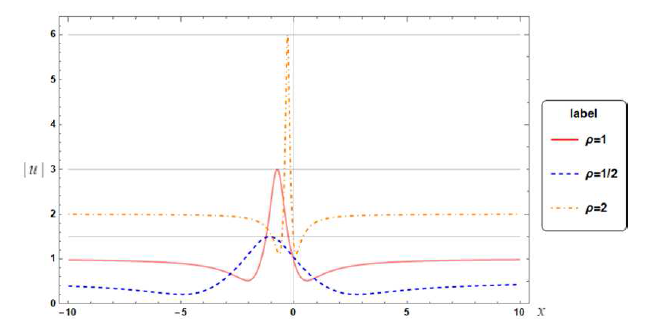
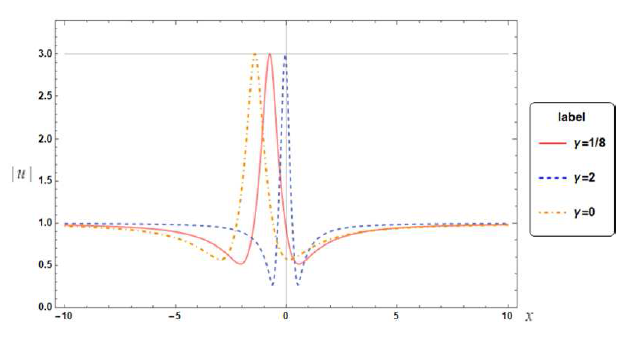
修正的非线性薛定谔方程(MNLS方程)与导数非线性薛定谔方程(DNLS 方程)是两个紧密相关且完全可积的非线性偏微分方程. 该文通过Hirota双线性导数变换方法, 首先求得MNLS 方程在平面简谐波背景下的空间周期解, 即Akhmediev型呼吸子解, 再通过长波极限得其Rogue波解. 根据简单的参数归零法使之自然地约化为DNLS 方程的Rogue波解, 并借助于一个积分变换将其变换为Chen-Lee-Liu方程的Rogue波解. 文章还简要讨论了MNLS方程和DNLS 方程在非局域情形整体解的存在性问题.

关键词: Rogue wave, MNLS 方程, DNLS方程, Hirota双线性导数变换, 空间周期解, 呼吸子解

Abstract:

The modified nonlinear Schrodinger (MNLS for brevity) equation and the Derivative nonlinear Schrodinger (DNLS for brevity) equation are two nonlinear differential equations that are closely correlated and fully integrable. Firstly, the spatially periodic breather solution of the MNLS equation has been obtained by method of Hirota's bilinear derivative transform, and then its rogue wave solution is also obtained by a long-wave limit of the Akhmediev-type breather, which can be naturally reduced to a rogue wave solution of the DNLS equation by a simple operation of parameters. The existence of global soliton/rogue wave solutions for the MNLS/DNLS equations is briefly discussed.

Key words: Rogue wave, MNLS equation, DNLS equation, Hirota's bilinear derivative transform, Spatially periodic solution, Breather

中图分类号:

O175.2

唐宇轩, 周国全. 用Hirota 双线性导数变换求MNLS 方程的Rogue 波解[J]. 数学物理学报, 2023, 43(1): 132-142.

Tang Yuxuan, Zhou Guoquan. The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation[J]. Acta mathematica scientia,Series A, 2023, 43(1): 132-142.

图/表 4

参考文献 38

[1]	Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Physics Letters A, 2009, 373(6): 675-678 doi: 10.1016/j.physleta.2008.12.036
[2]	Akhmediev N, Soto-Crespo J M, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Physics Letters A, 2009, 373(25): 2137-2145 doi: 10.1016/j.physleta.2009.04.023
[3]	Wen X Y, Yang Y, Yan Z. Generalized perturbation $(n, M)$-fold Darboux transformations and multi-rogue-wave structures for the modified self-steepening nonlinear Schrödinger equation. Physical Review E, 2015, 92(1): 012917 doi: 10.1103/PhysRevE.92.012917
[4]	Pan C, Bu L, Chen S, et al. General rogue wave solutions under SU (2) transformation in the vector Chen-Lee-Liu nonlinear Schrödinger equation. Physica D: Nonlinear Phenomena, 2022, 434: 133204 doi: 10.1016/j.physd.2022.133204
[5]	He J, Xu S, Cheng Y. The rational solutions of the mixed nonlinear Schrödinger equation. AIP Advances, 2015, 5(1): 017105 doi: 10.1063/1.4905701
[6]	Zhao L C, Guo B, Ling L. High-order rogue wave solutions for the coupled nonlinear Schrödinger equations-II. Journal of Mathematical Physics, 2016, 57(4): 043508 doi: 10.1063/1.4947113
[7]	Ankiewicz A, Akhmediev N. Rogue wave solutions for the infinite integrable nonlinear Schrödinger equation hierarchy. Physical Review E, 2017, 96(1): 012219 doi: 10.1103/PhysRevE.96.012219
[8]	Xu S, He J, Wang L. The Darboux transformation of the derivative nonlinear Schrödinger equation. Journal of Physics A: Mathematical and Theoretical, 2011, 44(30): 305203 doi: 10.1088/1751-8113/44/30/305203
[9]	Guo B, Ling L, Liu Q P. High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Studies in Applied Mathematics, 2013, 130(4): 317-344 doi: 10.1111/j.1467-9590.2012.00568.x
[10]	Zhang Y, Guo L, Xu S, et al. The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(6): 1706-1722 doi: 10.1016/j.cnsns.2013.10.005
[11]	Wang L H, Porsezian K, He J S. Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Physical Review E, 2013, 87(5): 053202 doi: 10.1103/PhysRevE.87.053202
[12]	Lou S, Lin J. Rogue waves in nonintegrable KdV-type systems. Chinese Physics Letters, 2018, 35(5): 050202 doi: 10.1088/0256-307X/35/5/050202
[13]	Wu H, Fei J, Ma W. Lump and rational solutions for weakly coupled generalized Kadomtsev-Petviashvili equation. Modern Physics Letters B, 2021, 35(26): 2150449 doi: 10.1142/S0217984921504492
[14]	Zhou G, Li X. Space periodic solutions and rogue wave solution of the derivative nonlinear Schrödinger equation. Wuhan University Journal of Natural Sciences, 2017, 22(5): 373-379 doi: 10.1007/s11859-017-1261-2
[15]	Ma W X. Nonlocal PT-symmetric integrable equations and related Riemann-Hilbert problems. Partial Differential Equations in Applied Mathematics, 2021, 4: 100190 doi: 10.1016/j.padiff.2021.100190
[16]	Ablowitz M J, Musslimani Z H. Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity, 2016, 29(3): 915 doi: 10.1088/0951-7715/29/3/915
[17]	Yang B, Yang J. Rogue waves in the nonlocal ${\mathcal {PT}} $ PT-symmetric nonlinear Schrödinger equation. Letters in Mathematical Physics, 2019, 109(4): 945-973 doi: 10.1007/s11005-018-1133-5
[18]	Lin J, Jin X W, Gao X L, et al. Solitons on a periodic wave background of the modified KdV-Sine-Gordon equation. Communications in Theoretical Physics, 2018, 70(2): 119-126 doi: 10.1088/0253-6102/70/2/119
[19]	Li L, Duan C, Yu F. An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation. Physics Letters A, 2019, 383(14): 1578-1582 doi: 10.1016/j.physleta.2019.02.031
[20]	Zhong W P, Yang Z, Beli${\rm\acute{c}}$ M, et al. Breather solutions of the nonlocal nonlinear self-focusing Schrödinger equation. Physics Letters A, 2021, 395: 127228 doi: 10.1016/j.physleta.2021.127228
[21]	Ma W X, Zhou R. A coupled AKNS-Kaup-Newell soliton hierarchy. Journal of Mathematical Physics, 1999, 40(9): 4419-4428 doi: 10.1063/1.532976
[22]	Chen Z Y, Huang N N. Explicit N-soliton solution of the modified nonlinear Schrödinger equation. Physical Review A, 1990, 41(7): 4066-4069 doi: 10.1103/PhysRevA.41.4066
[23]	Huang N N, Chen Z Y. Alfven solitons. Journal of Physics A: Mathematical and General, 1990, 23(4): 439-453 doi: 10.1088/0305-4470/23/4/014
[24]	Chen H H, Lee Y C, Liu C S. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Physica Scripta, 1979, 20(3/4): 490-492 doi: 10.1088/0031-8949/20/3-4/026
[25]	Kaup D J, Newell A C. An exact solution for a derivative nonlinear Schrödinger equation. Journal of Mathematical Physics, 1978, 19(4): 798-801 doi: 10.1063/1.523737
[26]	Kawata T, Inoue H. Exact solution of derivative nonlinear Schrödinger equation under nonvanishing conditions. J Phys Soc Jpn, 1978, 44(6): 1968-1976 doi: 10.1143/JPSJ.44.1968
[27]	Steudel H. The hierarchy of multi-soliton solutions of derivative nonlinear Schrödinger equation. J Phys A, 2003, 36: 1931-1946 doi: 10.1088/0305-4470/36/7/309
[28]	Zhou G Q, Huang N N. An $N$-soliton solution to the DNLS equation based on revised inverse scattering transform. Journal of Physics A: Mathematical and Theoretical, 2007, 40(45): 13607-13623 doi: 10.1088/1751-8113/40/45/008
[29]	Zhou G. A multi-soliton solution of the DNLS equation based on pure Marchenko formalism. Wuhan University Journal of Natural Sciences, 2010, 15(1): 36-42 doi: 10.1007/s11859-010-0108-x
[30]	Zhou G, Bi X. Soliton solution of the DNLS equation based on Hirota's bilinear derivative transform. Wuhan University Journal of Natural Sciences, 2009, 14(6): 505-510 doi: 10.1007/s11859-009-0609-7
[31]	蔡浩. 关于MNLS方程和DNLS方程的研究. 武汉大学, 2005
	Cai H. Research about MNLS Equation and DNLS Equation. Wuhan Univ, 2005
[32]	Chen X J, Lam W K. Inverse scattering transform for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions. Physical Review E, 2004, 69(6): 066604 doi: 10.1103/PhysRevE.69.066604
[33]	Chen X J, Yang J K, Lam W K. $N$-soliton solution for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions. Journal of Physics A: Math Gen, 2006, 39(13): 3263-3274 doi: 10.1088/0305-4470/39/13/006
[34]	Lashkin V M. $N$-soliton solutions and perturbation theory for DNLS with nonvanishing condition. J Phys A, 2007, 40: 6119-6132 doi: 10.1088/1751-8113/40/23/008
[35]	Zhou G. A newly revised inverse scattering transform for DNLS+ equation under nonvanishing boundary condition. Wuhan University Journal of Natural Sciences, 2012, 17(2): 144-150 doi: 10.1007/s11859-012-0819-2
[36]	Zhou G. Explicit breather-type and pure N-Soliton solution of DNLS+ equation with nonvanishing boundary condition. Wuhan University Journal of Natural Sciences, 2013, 18(2): 147-155 doi: 10.1007/s11859-013-0907-y
[37]	Osman M S, Almusawa H, Tariq K U, et al. On global behavior for complex soliton solutions of the perturbed nonlinear Schrödinger equation in nonlinear optical fibers. Journal of Ocean Engineering and Science, 2022, 7(5): 431-443 doi: 10.1016/j.joes.2021.09.018
[38]	Bourgain J. Global Solutions of Nonlinear Schrödinger Equations. Providence, RI: American Mathematical Society, 1999