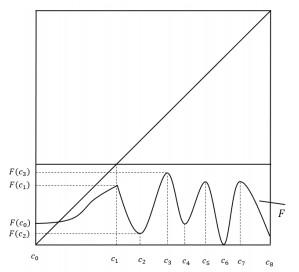
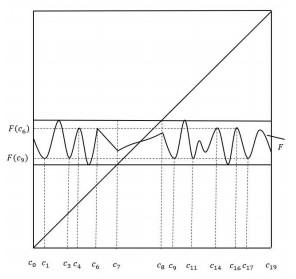
1 引言
令
其中
进一步, 如果
定理A[17, 定理4] 令
(K
(K
则对任意整数
表 1 没有特征端点条件下, 在[a′,b′]上严格递增的F连续迭代根的结果, 其中符号↑, ↓分别表示严格递增和严格递减.
| 阶数 | 存在性或不存在性 | |
| 不存在 | ||
| 存在 | ||
| 不存在 | ||
| 不存在 | ||
| 不存在 | ||
| 不存在 | ||
| 存在 | ||
| 不存在 | ||
| 不存在 |
本文的组织如下.在第2节中, 我们给出一个充分条件使得
2 主要结果
当
2.1 在特征区间上递增的迭代根
下面的定理2.1处理的情形是
定理2.1 设
这里
图 1
当
下面, 我们考虑
定理2.2 设
进一步假设存在非单调点
使得
并且除去
和非单调点
使得
并且除去
则
使得
和非单调点
使得
以上讨论表明图 2中的
图 2
2.2 在特征区间上递减的迭代根
定义2.1 令
(ⅰ)存在一个
(ⅱ)
(ⅲ)对任意一对相邻的不动点
与特征区间上递增的迭代根讨论一样, 我们先考虑特征区间为第一个单调区间的情形, 即
定理2.3 设
则
根据条件(2.15), 很容易验证定理2.3中的
图 3
类似地, 当最后一个单调区间
下面, 我们考虑
定理2.4 设
如果定理
3 辅助引理
在本节中, 我们给出一些将在第4节有用的引理.
引理3.1 令
证 由于情形
其中
引理3.2 令
证 我们仅证明
的函数
的一个连续严格递减解
显然, 对所有
是良定义的, 且在
另外,
现在, 我们定义一个本引理希望得到的函数.令
显然,
引理3.3[8, 引理3.1] 令
4 定理证明
本节我们将分别证明第2节中的定理2.1–2.4.
定理2.1的证明 第一步 在
在条件(2.1), (2.2) (或(2.3))下, 根据文献[6, 定理15.7]和引理3.1, 我们可以构造一个连续且严格递增的函数
并且对所有
第二步 在每个区间
对所有
根据(4.1)式和
对于
因为
因为
第三步 连接这些
对于
由(4.3)–(4.4)式, 我们可知
再利用(4.6)式, 我们有
最后由(4.7)式, 我们进一步得到
上述的讨论表明
定理2.2的证明 第一步 在
在条件(2.4), (2.5) (或者(2.6))下, 根据[6, 定理15.7]和引理3.1, 我们可以找到一个连续且严格递增的函数
并且对所有
第二步 在区间
对于
注意到
第三步 定义区间
对于
根据(2.9), (4.12), (4.13)和(4.8)式, 我们有
对于
由(2.10)和(4.8)式, 我们可知
对于
由(2.10), (4.10), (4.11)和(4.8)式容易验证(4.16)式中定义的
第四步 定义区间
对于
第五步 对于所有
在每个区间
为了证明
且
因此, 对于每一个
事实上, (4.19)式可由(4.14), (2.8)和(4.17)式得到, (4.20)式可由(4.10), (4.15), (2.8)和(4.18)式得到.这表明
这说明
这意味着
这意味着
接下来, 我们证明
定理2.3的证明 第一步 在
因为
并且对所有
第二步 在区间
定义
由于
第三步 对
对于每一个
注意
第四步 对所有
对所有
这表明
另一方面, 由于
对所有
这就证明了
最后, 由于在区间
定理2.4的证明 第一步 在
因为
并且对所有
第二步 在区间
第三步 在区间
第四步 在区间
第五步 连接上述函数可定义一个连续的两次迭代根.由于第二步到第五步和定理2.2的证明类似, 我们不再阐述.
参考文献
An Essay towards the calculus of functions
Recent results on functional equations in a single variable, perspectives and open problems
DOI:10.1007/s000100050159 [本文引用: 1]
The embedding of homeomorphisms in flows
DOI:10.1090/S0002-9939-1955-0080911-2
On the functional equation \varphi^n (x) = g(x)
DOI:10.4064/ap-11-2-161-175 [本文引用: 1]
Iterative roots of piecewise monotonic functions with finite nonmonotonicity height
DOI:10.1016/j.jmaa.2013.09.051 [本文引用: 1]
A note on iterative roots of PM functions
DOI:10.1016/j.jmaa.2007.11.006 [本文引用: 2]
The question on characteristic endpoints for iterative roots of PM functions
DOI:10.1016/j.jmaa.2017.09.009 [本文引用: 2]
Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2
DOI:10.1016/j.na.2011.08.033 [本文引用: 2]
General theorem for the existence of iterative roots of homeomorphisms with periodic points
DOI:10.1016/j.jmaa.2012.03.048 [本文引用: 1]
Recent results on iteration theory: iteration groups and semigroups in the real case
DOI:10.1007/s00010-013-0186-x [本文引用: 1]
PM functions, their characteristic intervals and iterative roots
DOI:10.4064/ap-65-2-119-128 [本文引用: 4]