1 绪论
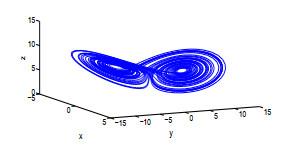
Rabinovich系统源自于国际知名学者Pikovski、Rabinovich和Trakhtengerts在研究等离子体中三种共振耦合波相互作用问题时, 发现下述动力学方程(其常被简称为PRT系统)能准确地描述平行于磁场的等离子体波与离子声波的相互作用, 以及等离子体在低杂化共振附近的振荡的等离子体动力学行为[1]:
图 1
当前研究动力系统稳定性的两大高效方法当属Lyapunov稳定性理论和KCC理论. Lyapunov稳定性理论[6-7]是研究描述动力系统的微分方程的解的稳定性非常成熟的技术, 其也常运用于研究系统的混沌行为, 如正向不变集和分形维数的估计等. 此外, 在刻画关于系统平衡点的几何结构时, 往往引进Lyapunov指数, 使之能并量化地给出轨迹的指数偏差. 但对于"混沌: 对于初始值的极度敏感性是如何与经典的不稳定性联系起来的呢?" 这个问题, 有学者认为经典Lyapunov不稳定性定理已不足以充分描述这些现象的本质[8-9], 特别是近期关于只有稳定平衡点或甚至没有平衡点的混沌系统和隐藏吸引子概念的问题的引入.
KCC理论是源于Kosambi[10], Cartan[11]和Chern[12]的开创性工作所提出的一种研究动力系统稳定性的几何动力学方法(geometrodynamical approach), 其基本思想是考虑到二阶动力系统与相关Finsler空间中的测地线方程之间存在一一对应关系. 准确而言, 其是构建整体轨迹偏离附近轨迹的变分方程的微分几何理论. 从动力系统的几何描述而言, 其将非线性联络和Berwald联络关联到微分系统中, 从而获得五个几何不变量. 其中, 第二个不变量, 也被称为偏离曲率张量, 能准确刻画系统的Jacobi稳定性(KCC理论也常被称为Jacobi分析方法). Jacobi稳定性事实上是将测地线流在具有度量(黎曼(Riemann)或芬斯勒(Finsler))的可微流形上的稳定性推广至非度量上的一种自然演化, 进而构成了KCC理论的重要组成部分[13]. Jacobi分析方法是从系统轨迹的任何一点出发, 通过计算系统轨迹偏离曲率张量所构成的不变量: 线性化特征值, 根据特征值的实部的符号来判断系统的稳定性. 可见它不仅能分析系统平衡点的稳定性, 也能分析没有平衡点的系统的轨线上任意一点处的稳定性情况. 这给含隐藏吸引子[14]系统的复杂性分析提供了一种很好的几何方法. 事实上, Maria等人自1997年开始建立了一个理论框架[15], 致力于动力系统行为的几何描述以及它们的混沌特性.
近年来, 从几何角度出发探究系统轨线的复杂性的研究越来越受关注[16-19]. 早期, KCC理论主要应用在二维系统中, 包括生物系统[20]、化学系统[21]. 后来逐渐应用到了宇宙学[22]、力学[23-24]、天体物理学[25]、医学[26]等领域的研究中[27]. 目前, KCC理论主要集中应用到三维的混沌系统, 如Lorenz系统[28], Hamiltonian系统[29], Rössler系统[30], Rikitake系统[31-32], Chua系统[33]和其他的三维混沌系统[34-37]. 值得提及, 文献[17, 28]指出偏离矢量的曲率通过从正值到负值的过渡, 本质上同轨线的混沌行为存在紧密联系, 早期的过渡意味着混沌的发生.
2 KCC理论和Jacobi稳定性
令
其中
定义
其中,
运用KCC协变微分和方程(2.5), 可得
其中
这里
在几何上, 可以把第三个KCC不变量
在欧几里得空间
假设
不难看出,
于是, 轨线在
3 Jacobi稳定性
首先, 通过简单计算可知: 当
其中
下面利用KCC理论, 讨论Rabinovich系统(1.1)平衡点的Jacobi稳定性. 全文假设所有参数
由系统(1.1)可得
令
因此, 可将系统(3.2)简记为
其中
通过计算, 不难得出
由于上述非线性联络的每一分量均与
同时运用(2.7)式, 得到偏离曲率张量(第二个KCC不变量)分量
在Rabinovich系统中, 显然可知(2.8)式的第三、第四和第五个KCC不变量均为零.
相似地, 在平衡点
故, 可将系统的第二个KCC不变量(偏离曲率张量)写成下述矩阵形式
其特征多项式为
沿用上述形式, 可计算出Rabinovich系统在平衡点
该矩阵的特征多项式为
其中
于是根据Routh-Hurwitz判别法则, 可知在指定的参数条件下, 平衡点
且
通过选取参数
表 1
Rabinovich系统平衡点的稳定性(
| 参数取值 | 平衡点 | 线性稳定性态 | Jacobi稳定性态 |
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 | ||
| 不稳定 | 不稳定 |
从表 1可以看出, 在给定的四组参数条件下, 平衡点
4 混沌分析
本节将通过分析偏离向量、偏离向量曲率和不稳定性指数的时间演化对Rabinovich系统(1.1)的混沌属性进行直观的探讨.
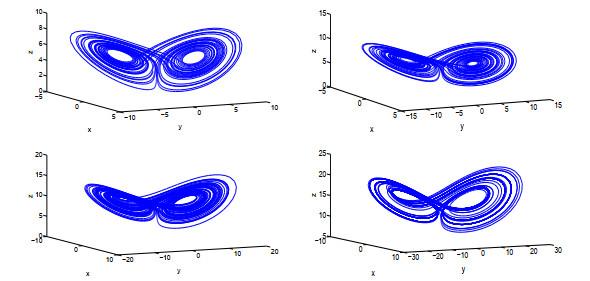
图 2
图 2
Rabinovich系统混沌吸引子的相图(
此外结合方程(2.5)可得, Rabinovich系统的偏离向量
其中偏离向量
为了定量刻画系统的混沌机理, 在此引入不稳定指数
将平衡点
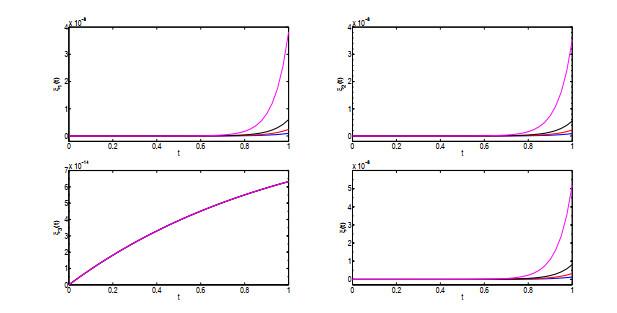
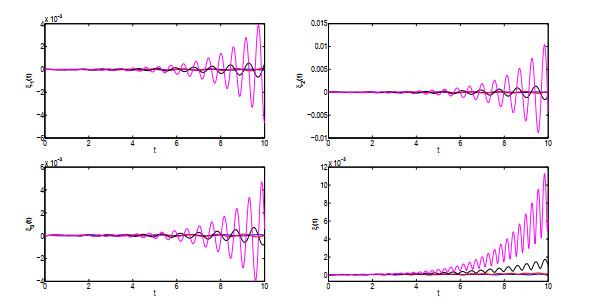
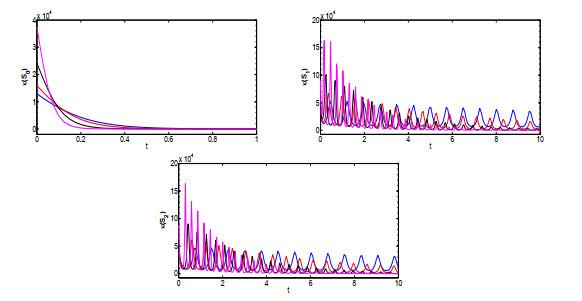
图 3呈现了系统在平衡点
图 3
图 3
偏离向量
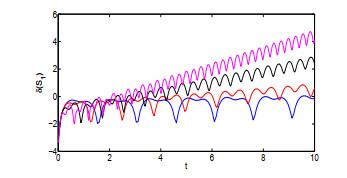
图 4
图 4
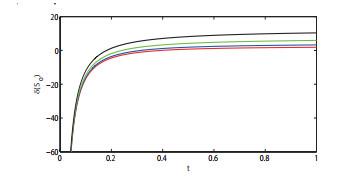
不稳定性指数
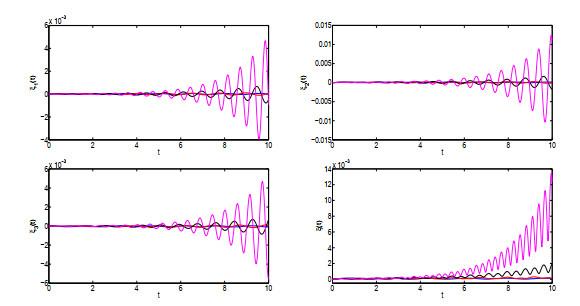
同样地, 通过方程(4.1)–(4.3)可获得偏离向量在平衡点
图 5
图 5
偏离向量
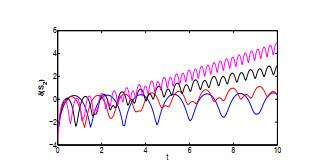
图 6
图 6
不稳定性指数
相似地, 偏离向量在平衡点
图 7
图 7
偏离向量
图 8
图 8
不稳定性指数
另一方面, 考虑到偏离向量的曲率也可以很好地描述系统的混沌属性(参见文献[28]), 故, 根据微分几何的标准方法, 用曲线
由图 9可以看出, Rabinovich系统曲线的偏离方式是呈线性的, 即沿着其切线方向偏离.
图 9
图 9
在平衡点
5 结论
本文基于KCC理论将微分几何技术应用到三维多项式系统的混沌复杂性研究. 论文从系统轨线的任意点出发分析了三维Rabinovich系统的Jacobi稳定性态, 结果表明, 系统在原点
参考文献
Onset of stochasticity in decay confinement of parametric instability
Integrals of motion and semipermeable surfaces to bound the amplitude of a plasma instability
DOI:10.1103/PhysRevE.63.036202 [本文引用: 4]
Estimation of the domain containing all compact invariant sets of a system modelling the amplitude of a plasma instability
On the global dynamics of the Rabinovich system
DOI:10.1088/1751-8113/41/27/275210 [本文引用: 1]
The general problems of the stability of motion
DOI:10.1080/00207179208934253 [本文引用: 1]
A.M. Lyapunov's stability theory-100 years on
DOI:10.1093/imamci/9.4.275 [本文引用: 1]
Parallelism and path-spaces
DOI:10.1007/BF01474602 [本文引用: 1]
Observations sur le mémoire précédent
DOI:10.1007/BF01474603 [本文引用: 1]
Sur la geometrie d'un systeme d'equations differentielles du second ordre
Jacobi stability analysis of dynamical systems-applications in gravitation and cosmology
Hidden attractor in smooth Chua systems
DOI:10.1016/j.physd.2012.05.016 [本文引用: 1]
Dynamical behavior of Lagrangian systems on Finsler manifolds
DOI:10.1103/PhysRevE.55.6448 [本文引用: 1]
n-维分段光滑微分系统的周期轨分支
DOI:10.3969/j.issn.1003-3998.2020.04.019 [本文引用: 1]
Bifurcation of periodic orbits of an n-dimensional piecewise smooth differential system
DOI:10.3969/j.issn.1003-3998.2020.04.019 [本文引用: 1]
一类新混沌系统的几何分析
Geometric analysis of a class of the new chaotic system
三种群捕食-食饵模型的分形特征与控制
DOI:10.3969/j.issn.1003-3998.2019.04.022
Fractal feature and control three-species predator-prey model
DOI:10.3969/j.issn.1003-3998.2019.04.022
一类三次Hamiton系统的极限环分支
Limit cycle bifurcations for a kind of Hamiton systems of degree three
Lotka-Volterra system and KCC theory: Differential geometric structure of competitions and predations
DOI:10.1016/j.nonrwa.2012.11.015 [本文引用: 1]
Some remarks on Jacobi stability
Jacobi stability of the vacuum in the static spherically symmetric brane world models
DOI:10.1103/PhysRevD.77.104009 [本文引用: 1]
Dynamical behavior and Jacobi stability analysis of wound strings
DOI:10.1140/epjc/s10052-016-4148-z [本文引用: 1]
Jacobi stability of circular orbits in central forces
DOI:10.1080/1726037X.2012.10698621 [本文引用: 1]
Nonlinear stability analysis of the Emden-Fowler equation
KCC theory and its application in a tumor growth model
DOI:10.1002/mma.4542 [本文引用: 1]
New results about the geometric invariants in KCC-theory
Jacobi stability analysis of the Lorenz system
Jacobi stability of Hamiltonian system
Jacobi stability analysis of Rössler system
Geometrical unified theory of Rikitake system and KCC-theory
DOI:10.1016/j.na.2008.10.017 [本文引用: 1]
Jacobi stability analysis of Rikitake system
DOI:10.1142/S0219887816500985 [本文引用: 1]
Jacobi stability analysis of modified Chua circuit system
Stability analysis of Navier-Stokes system
DOI:10.1142/S0219887819501573 [本文引用: 1]
Jacobi stability analysis of Chen system
New insights into a chaotic system with only a Lyapunovstable equilibrium