数学物理学报 ›› 2021, Vol. 41 ›› Issue (3): 783-796.
Rabinovich系统的Jacobi分析
刘永建1,*(
),黄秋健2
- 1 玉林师范学院 广西高校复杂系统优化与大数据处理重点实验室 广西玉林 537000
2 广西民族大学理学院 & 广西大学附属中学 南宁 530006
-
收稿日期:2020-03-08出版日期:2021-06-26发布日期:2021-06-09 -
通讯作者:刘永建 E-mail:liuyongjianmaths@126.com -
基金资助:国家自然科学基金(11961074);广西自然科学基金重点项目(2018GXNSFDA281028);广西高校高水平创新团队项目([2018]35);玉林师范学院高层次人才启动项目(G2019ZK51)
Jacobi Analysis of the Rabinovich System
Yongjian Liu1,*(),Qiujian Huang2
- 1 Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing, Yulin Normal University, Guangxi Yulin 537000
2 College of Sciences, Guangxi University for Nationalities & High School Affiliated to Guangxi University, Nanning 530006
-
Received:2020-03-08Online:2021-06-26Published:2021-06-09 -
Contact:Yongjian Liu E-mail:liuyongjianmaths@126.com -
Supported by:the NSFC(11961074);the NSF of Guangxi Province(2018GXNSFDA281028);the High Level Innovation Team Program from Guangxi Higher Education Institutions of China([2018]35);the Senior Talent Research Foundation of Yulin Normal University(G2019ZK51)
摘要：
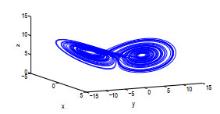
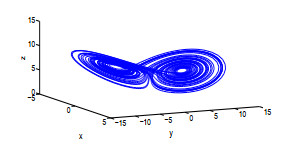
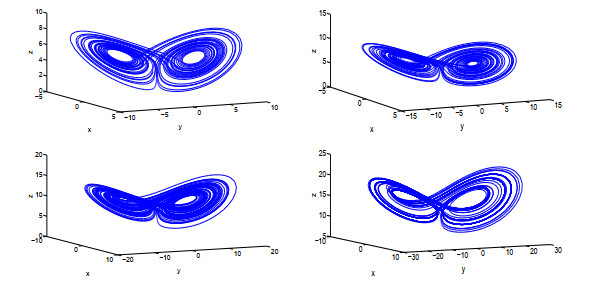
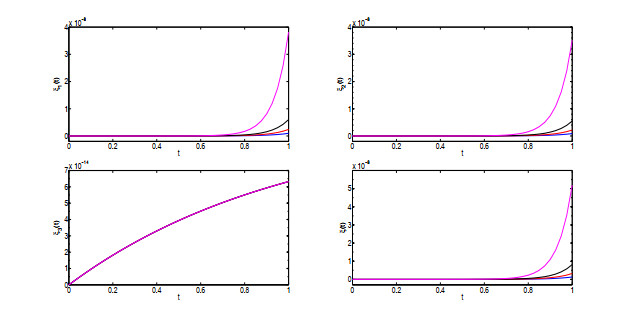
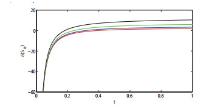
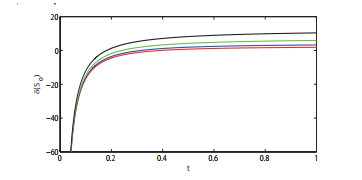
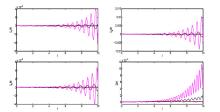
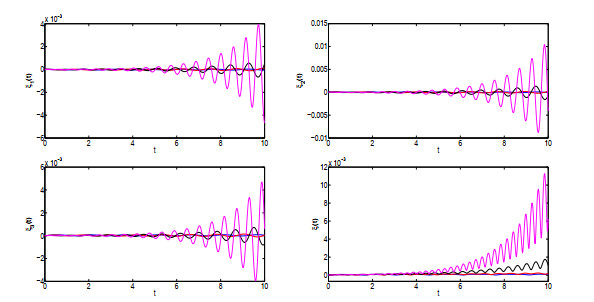
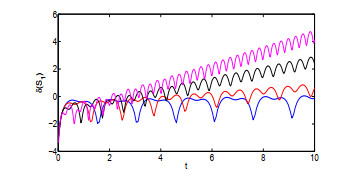
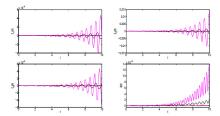
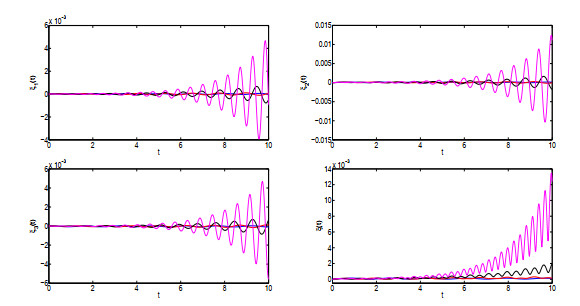
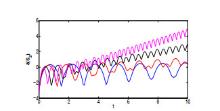
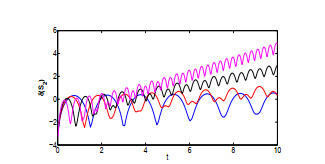
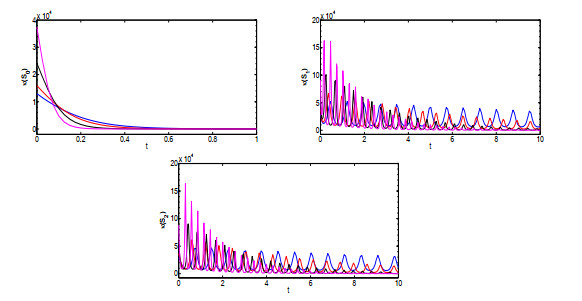
该文运用微分几何技术开展三维微分系统的复杂性研究.基于Kosambi-Cartan-Chern（KCC）理论，从系统轨线的任意点出发，分析三维Rabinovich系统的Jacobi稳定性态，并给出系统所有平衡点的Jacobi稳定的条件；在获得系统平衡点附近偏离向量及其分量的时间演化的基础上，通过引入不稳定性指数和曲率，同时结合数值仿真对系统的混沌机理进行探讨性分析，数值结果有力地验证了已有的理论分析结果.
中图分类号:
- O175
引用本文
刘永建,黄秋健. Rabinovich系统的Jacobi分析[J]. 数学物理学报, 2021, 41(3): 783-796.
Yongjian Liu,Qiujian Huang. Jacobi Analysis of the Rabinovich System[J]. Acta mathematica scientia,Series A, 2021, 41(3): 783-796.
图 1
Rabinovich系统混沌吸引子的相图($ v_{1} = 1 $, $ v_{2} = 4 $, $ v_{3} = 1 $, $ h = 6.75 $)"
表 1
Rabinovich系统平衡点的稳定性($v_1 = v_3 = 1$, $v_2 = 4$)"
| 参数取值 | 平衡点 | 线性稳定性态 | Jacobi稳定性态 |
| | 不稳定 | 不稳定 | |
| | 不稳定 | 不稳定 | |
| | | 不稳定 | 不稳定 |
| | 不稳定 | 不稳定 | |
| | | 不稳定 | 不稳定 |
| | 不稳定 | 不稳定 | |
| | 不稳定 | 不稳定 | |
| | 不稳定 | 不稳定 |
图 2
Rabinovich系统混沌吸引子的相图($v_{1} = 1$, $v_{2} = 4$, $v_{3} = 1$, $h = 5.5$(左上); $h = 6.75$(右上); $h = 10$(左下); $h = 15$(右下))."
图 3
偏离向量$ \xi $及其分量$ \xi_{i} $在平衡点$ S_{0} $附近的时间演化, $ i = 1, 2, 3 $. $ v_{1} = 1, v_{2} = 4, $ $ v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-13} $."
图 4
不稳定性指数$ \delta(S_{0}) $的时间演化结果. $ v_{1} = 1, v_{2} = 4, v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-13} $."
图 5
偏离向量$ \xi $及其分量$ \xi_{i} $在平衡点$ S_{1} $附近的时间演化, $ i = 1, 2, 3 $. $ v_{1} = 1, v_{2} = 4, $ $ v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-4} $."
图 6
不稳定性指数$ \delta(S_{1}) $的时间演化. $ v_{1} = 1, v_{2} = 4, v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-4} $."
图 7
偏离向量$ \xi $及其分量$ \xi_{i} $在平衡点$ S_{2} $附近的时间演化, $ i = 1, 2, 3 $. $ v_{1} = 1, v_{2} = 4, $ $ v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-4} $."
图 8
不稳定性指数$ \delta(S_{2}) $的时间演化. $ v_{1} = 1, v_{2} = 4, v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-4} $."
图 9
在平衡点$ S_{0} $(左上), $ S_{1} $(右上), $ S_{2} $(下方)处的曲率的时间演化. $ v_{1} = 1, v_{2} = 4, $ $ v_{3} = 1 $, $ h = 5.5 $(蓝色曲线); $ h = 6.75 $(红色曲线); $ h = 10 $(黑色曲线); $ h = 15 $(紫色曲线). 初始条件$ \xi_{1}(0) = \xi_{2}(0) = \xi_{3}(0) = 0 $, $ \dot{\xi}_{1}(0) = \dot{\xi}_{2}(0) = \dot{\xi}_{3}(0) = 10^{-4} $."
| 1 | Pikovski A S , Rabinovich M I , Trakhtengerts Yu V . Onset of stochasticity in decay confinement of parametric instability. Soviet Physics-JETP, 1978, 47 (4): 715- 719 |
| 2 | Boichenko V A, Leonov G A, Reitmann V. Dimension Theory for Ordinary Differential Equations. Stuttgart: Teubner, 2005 |
| 3 |
Neukirch S . Integrals of motion and semipermeable surfaces to bound the amplitude of a plasma instability. Physical Review E, 2001, 63 (3): 036202
doi: 10.1103/PhysRevE.63.036202 |
| 4 | Krishchenko A , Starkov K . Estimation of the domain containing all compact invariant sets of a system modelling the amplitude of a plasma instability. Physics Letters A, 2007, 367 (1): 65- 72 |
| 5 |
Llibre J , Messias M , Silva P R . On the global dynamics of the Rabinovich system. Journal of Physics A: Mathemetical and Theorerical, 2008, 41 (27): 275210
doi: 10.1088/1751-8113/41/27/275210 |
| 6 |
Lyapunov A M . The general problems of the stability of motion. Int J Control, 1992, 55 (3): 531- 773
doi: 10.1080/00207179208934253 |
| 7 |
Parks P C . A.M. Lyapunov's stability theory-100 years on. IMA J Math Control and Inform, 1992, 9 (4): 275- 303
doi: 10.1093/imamci/9.4.275 |
| 8 | Fradkov A L, Pogromsky A Y. Introduction to Control of Oscillation and Chaos. Singapore: World Scientific, 1998 |
| 9 | Leonov G A. Strange Attractors and Classical Stability Theory. St Petersburg: St Petersburg University Press, 2009 |
| 10 |
Kosambi D D . Parallelism and path-spaces. Mathematische Zeitschrift, 1933, 37 (1): 608- 618
doi: 10.1007/BF01474602 |
| 11 |
Cartan E . Observations sur le mémoire précédent. Mathematische Zeitschrift, 1933, 37 (1): 619- 622
doi: 10.1007/BF01474603 |
| 12 | Chern S S . Sur la geometrie d'un systeme d'equations differentielles du second ordre. Bulletin des Sciences Mathematiques, 1939, 63, 206- 212 |
| 13 | Boehmer C G , Harko T , Sabau V S . Jacobi stability analysis of dynamical systems-applications in gravitation and cosmology. Advances in Theoretical and Mathematical Physics, 2010, 16 (4): 1145- 1196 |
| 14 |
Leonov G A , Kuznetsov N V , Vagaitsev V I . Hidden attractor in smooth Chua systems. Physica D, 2012, 241 (18): 1482- 1486
doi: 10.1016/j.physd.2012.05.016 |
| 15 |
Maria D B , Dino B , Piero C , Giuseppe P . Dynamical behavior of Lagrangian systems on Finsler manifolds. Physical Review E, 1997, 55 (6): 6448- 6458
doi: 10.1103/PhysRevE.55.6448 |
| 16 |
杨纪华, 张二丽. n-维分段光滑微分系统的周期轨分支. 数学物理学报, 2020, 40A (4): 1043- 1052
doi: 10.3969/j.issn.1003-3998.2020.04.019 |
|
Yang J , Zhang E . Bifurcation of periodic orbits of an n-dimensional piecewise smooth differential system. Acta Math Sci, 2020, 40A (4): 1043- 1052
doi: 10.3969/j.issn.1003-3998.2020.04.019 |
|
| 17 | 黄燮桢, 刘永建, 黄秋健. 一类新混沌系统的几何分析. 数学物理学报, 2019, 39A (2): 339- 347 |
| Huang X , Liu Y , Huang Q . Geometric analysis of a class of the new chaotic system. Acta Math Sci, 2019, 39A (2): 339- 347 | |
| 18 |
邵长旭, 刘树堂. 三种群捕食-食饵模型的分形特征与控制. 数学物理学报, 2019, 39A (4): 951- 962
doi: 10.3969/j.issn.1003-3998.2019.04.022 |
|
Shao C , Liu S . Fractal feature and control three-species predator-prey model. Acta Math Sci, 2019, 39A (4): 951- 962
doi: 10.3969/j.issn.1003-3998.2019.04.022 |
|
| 19 | 张二丽, 邢玉清. 一类三次Hamiton系统的极限环分支. 数学物理学报, 2017, 37A (4): 825- 833 |
| Zhang E , Xing Y . Limit cycle bifurcations for a kind of Hamiton systems of degree three. Acta Math Sci, 2017, 37A (4): 825- 833 | |
| 20 |
Yamasaki K , Yajima T . Lotka-Volterra system and KCC theory: Differential geometric structure of competitions and predations. Nonlinear Analysis: Real World Applications, 2013, 14 (4): 1845- 1853
doi: 10.1016/j.nonrwa.2012.11.015 |
| 21 | Sabau V S . Some remarks on Jacobi stability. Nonlinear Analysis: Theory Methods & Applications, 2005, 63 (5-7): e143- e153 |
| 22 |
Harko T , Sabau V S . Jacobi stability of the vacuum in the static spherically symmetric brane world models. Physical Review D, 2008, 77 (10): 104009
doi: 10.1103/PhysRevD.77.104009 |
| 23 |
Lake M J , Harko T . Dynamical behavior and Jacobi stability analysis of wound strings. European Physical Journal C: Particles and Fields, 2016, 76, 1- 26
doi: 10.1140/epjc/s10052-016-4148-z |
| 24 |
Abolghasem H . Jacobi stability of circular orbits in central forces. Journal of Dynamical Systems and Geometric Theories, 2012, 10 (2): 197- 214
doi: 10.1080/1726037X.2012.10698621 |
| 25 | Bohmer C G , Harko T . Nonlinear stability analysis of the Emden-Fowler equation. Journal of Nonlinear Mathematical Physics, 2010, 17 (4): 503- 516 |
| 26 |
Gupta M K , Yadav C K . KCC theory and its application in a tumor growth model. Mathematical Methods in the Applied Sciences, 2017, 40, 7470- 7487
doi: 10.1002/mma.4542 |
| 27 | Antonelli P L , Bucataru I . New results about the geometric invariants in KCC-theory. Analele Stiintifice ale Universitatii Al I Cuza din Iasi-Matematica, 2001, 47 (2): 405- 420 |
| 28 | Harko T , Ho C Y , Leung C S , Yip S . Jacobi stability analysis of the Lorenz system. International Journal of Geometric Methods in Modern Physics, 2015, 12 (7): 55- 72 |
| 29 | Abolghasem H . Jacobi stability of Hamiltonian system. International Journal of Pure and Applied Mathematics, 2013, 87 (1): 181- 194 |
| 30 | Gupta M K , Yadav C K . Jacobi stability analysis of Rössler system. International Journal of Bifurcation and Chaos, 2017, 27 (4): 63- 76 |
| 31 |
Yajima T , Nagahama H . Geometrical unified theory of Rikitake system and KCC-theory. Nonlinear Analysis, 2009, 71, 203- 210
doi: 10.1016/j.na.2008.10.017 |
| 32 |
Gupta M K , Yadav C K . Jacobi stability analysis of Rikitake system. International Journal of Geometric Methods in Modern Physics, 2016, 13 (7): 1650098
doi: 10.1142/S0219887816500985 |
| 33 | Gupta M K , Yadav C K . Jacobi stability analysis of modified Chua circuit system. International Journal of Geometric Methods in Modern Physics, 2017, 14 (6): 121- 142 |
| 34 |
Kumar M , Mishra T N , Tiwari B . Stability analysis of Navier-Stokes system. International Journal of Geometric Methods in Modern Physics, 2019, 16 (10): 1950157
doi: 10.1142/S0219887819501573 |
| 35 |
Huang Q , Liu A , Liu Y . Jacobi stability analysis of Chen system. International Journal of Bifurcation and Chaos, 2019, 29 (10): 1950139
doi: 10.1142/S0218127419501396 |
| 36 | Chen B , Liu Y , Wei Z , Feng C . New insights into a chaotic system with only a Lyapunovstable equilibrium. Mathematical Methods in the Applied Sciences, 2020, 43 (2): 1- 18 |
| 37 | Liu Y, Chen H, Lu X, et al. Homoclinic orbits and Jacobi stability on the orbits of Maxwell-Bloch system. Applicable Analysis, 2020. DOI: 10.1080/00036811.2020.1854235 |
| 38 | Antonelli P L. Handbook of Finsler Geometry. Dordrecht: Kluwer Academic, 2003 |
| [1] | 桑利恒,陈振龙,郝晓珍. 双分数布朗运动重整化自相交局部时的光滑性[J]. 数学物理学报, 2020, 40(3): 796-810. |
| [2] | 王贺元. 平面不可压缩Navier-Stokes方程五模系统的力学机理及能量演化[J]. 数学物理学报, 2020, 40(2): 315-327. |
| [3] | 王贺元. Couette-Taylor流的力学机理与能量转换[J]. 数学物理学报, 2020, 40(1): 243-256. |
| [4] | 王志,闫理坦,余显烨. 分数噪声驱动的随机热方程解的局部时[J]. 数学物理学报, 2019, 39(3): 582-595. |
| [5] | 黄燮桢,刘永建,黄秋健. 一类新混沌系统的几何分析[J]. 数学物理学报, 2019, 39(2): 339-347. |
| [6] | 王建军. ∑(X)上权移位算子的不变分布混沌性[J]. 数学物理学报, 2018, 38(3): 446-453. |
| [7] | 姚玉武, 陈秀, 牛欣. 复扇形指标集上的分布混沌[J]. 数学物理学报, 2017, 37(5): 950-961. |
| [8] | 吴新星. 关于弱Specification性质的一个注记[J]. 数学物理学报, 2017, 37(4): 601-606. |
| [9] | 杨纪华, 张二丽, 刘媚. 具时滞反馈金融系统的动力学分析与混沌控制[J]. 数学物理学报, 2017, 37(4): 767-782. |
| [10] | 王贺元, 崔进. 旋转流动混沌行为的全局稳定性分析及数值仿真[J]. 数学物理学报, 2017, 37(4): 783-792. |
| [11] | 王贺元. 平面不可压缩磁流体动力学五模类Lorenz方程组的动力学行为及其数值仿真[J]. 数学物理学报, 2017, 37(1): 199-216. |
| [12] | 吴新星, 王建军. 关于P-极小动力系统的一些注记[J]. 数学物理学报, 2016, 36(5): 879-885. |
| [13] | 尹逊武, 李德生. 小时滞梯度系统的动力学行为[J]. 数学物理学报, 2015, 35(3): 464-477. |
| [14] | 卢天秀, 朱培勇, 吴新星. 非自治离散系统的分布混沌性[J]. 数学物理学报, 2015, 35(3): 558-566. |
| [15] | 冯春华. 一类简化的n个神经元时滞BAM神经网络模型的振动性[J]. 数学物理学报, 2011, 31(6): 1490-1501. |
|